基于层合参数的工字型加筋壁板稳定性设计
2019-02-07王佩艳岳春霞耿小亮杨白凤岳珠峰
王佩艳,岳春霞,耿小亮,杨白凤,岳珠峰
(西北工业大学力学与土木建筑学院 飞行器结构完整性技术工业和信息化部重点实验室,陕西 西安 710129)
1 前 言
复合材料具有比强度高、比刚度大、可设计性强等优点,在航空、航天、军事、机械等领域得到了广泛应用[1-3]。而复合材料加筋壁板是一种典型的承载结构,具有较高的抗弯刚度和较小的结构重量,显著提高了结构的使用效率,因此,广泛应用于对刚度和强度要求较大的平板或曲壳结构中,例如机翼、尾翼的翼面,梁腹板和机身上的蒙皮、隔框,以及火箭舱体等部位。加筋壁板的结构性能分析和设计技术是复合材料结构设计的关键[4]。
为了充分发挥复合材料加筋壁板的应用潜力,需要对结构进行优化设计,近几十年来很多学者开展了复合材料方面的优化设计工作[5-6]。复合材料层合板的设计变量包括铺层厚度和铺层顺序,如果直接以铺层顺序为设计变量进行包括强度、刚度、稳定性和频率等约束条件下的优化设计,设计变量多,单次运行时间长,优化设计所需的运行时间几乎是不可接受的。为了解决优化效率的问题,在复合材料层合板的优化设计中,通常将层合板厚度当作连续变量,采用分级优化策略进行铺层顺序的优化。分级优化的基本思路是首先开展以铺层厚度、铺层角、层合参数为设计变量的轻量化设计,然后以层合参数(主要是弯曲刚度系数)为目标,进行铺层顺序的优化。Cezar[7]等忽略耦合参数对稳定性的影响,以面内刚度系数和弯曲刚度系数为设计变量对复合材料板进行优化设计,然后以最优层合参数为目标采用数学准则法进行层合板的铺层顺序优化。J.Enrique Herencia[8-9]和Todoroki[10]将两级优化方法应用于加筋壁板的设计中,首先对蒙皮、筋条缘条和腹板的铺层厚度及层合参数(面内刚度系数和弯曲刚度系数)进行优化,然后以弯曲刚度系数为目标,进行铺层顺序优化。国内很多研究者也采用了分级优化。飞机强度研究所[11]采用COMPASS 优化软件,提出了以层合板分层为基本单位,用满应变准则设计层板厚度,以应变能调整分层比例的二级优化策略。李为吉[12]提出了复合材料结构优化的多级优化方法,系统级优化采用优化准则法得到最优铺层厚度,在元件级优化中用线性规划技术提高结构的应变能,从而得到最优的分层厚度。修英姝、崔德刚[13]等人首先用神经网络模型确定铺层数,然后采用遗传算法优化得到铺层顺序,董永朋[14]等采用beam 单元模拟复合材料加筋壁板,并进行多目标优化设计。
近些年来,国内在复合材料优化设计方面取得了较为丰硕的成果,更多的优化方法将应用于复合材料的优化设计中。但是多级优化方法的计算过程较为复杂,而且在两级之间有可能因为缺乏必要约束造成多级优化无法进行。复合材料层合板铺层顺序优化是典型的离散变量优化问题,无法采用常规的准则法或梯度法。Todoroki[10]应用分枝界限法对复合材料机翼进行了铺层顺序优化研究,但只适用于铺层层数比较少的情况。Cezar[7]采用BSGS中的黄金分割方法,以面内刚度系数和弯曲刚度系数为目标,进行了铺层顺序优化。A.Rama[15]采用蚁群优化算法进行了铺层顺序优化。穆朋刚[16]等将蚁群算法引入复合材料层合板铺层顺序的优化设计中,采用遗传算法的整数编码方法,将层合板的铺层顺序优化问题转化为求解旅行商(TSP)问题,然后采用改进后的蚁群算法进行优化设计。王伟[17]采用蚁群算法进行了T 形加筋壁板的优化设计。国内外对复合材料加筋壁板的优化设计多采用二级优化方法,集中研究铺层顺序的最优化问题,均未考虑加工工艺特征。本研究针对复合材料工字型加筋壁板的结构特点,建立了考虑工艺特征的仿真模型,然后采用二级优化策略对复合材料工字型加筋壁板进行了优化设计,在第二级优化过程中采用改进的遗传算法进行了离散变量的复合材料铺层顺序优化设计。
2 层合参数定义
在单向板材料性能确定的情况下,层合板的性能仅与铺层角度和铺层厚度有关。为了直观起见,可将面内刚度、耦合刚度和弯曲刚度等刚度性能以材料不变量和层合参数的形式表示。层合参数完全反映该层合板的面内、弯曲和耦合性能,一般将层合参数作为中间变量进行层合板的铺层优化设计。
层合板的偏轴刚度矩阵为
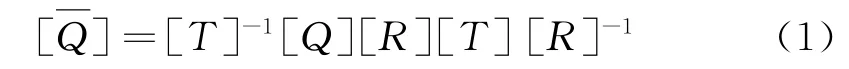
其中,[Q]为正轴刚度矩阵,[T]为转换矩阵,[R]为路透矩阵。 将层合板铺层角度代入公式(1)并展开,得到公式(2)。层合板的偏轴刚度矩阵仅与铺层角度和材料不变量有关。

其中:U为材料不变量,仅与单向板刚度有关,如式(3)所示。

层合板内力与应变关系如式(4)所示。

式中,{N}为层合板中面合力列阵;{M}为层合板中面合力矩列阵;{ε0}为层合板中面应变列阵;{κ}为层合板中面曲率列阵;[A]为层合板面内刚度矩阵;[B]为层合板拉弯耦合矩阵。

将式(2)代入式(4),得到层合板的面内刚度列阵、耦合刚度列阵和弯曲刚度列阵,如式(5)~式(7)所示。

为简单起见,将式(5)~式(7)中的求和公式用单一符号表示,分别得到层合参数,即面内刚度系数耦 合 参 数弯 曲 刚 度系数如式(8)~(10)所示。
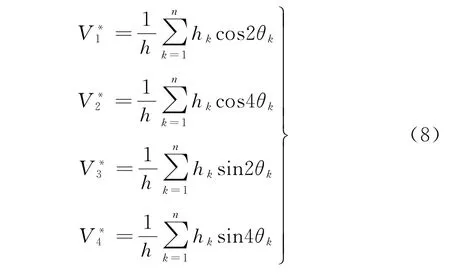
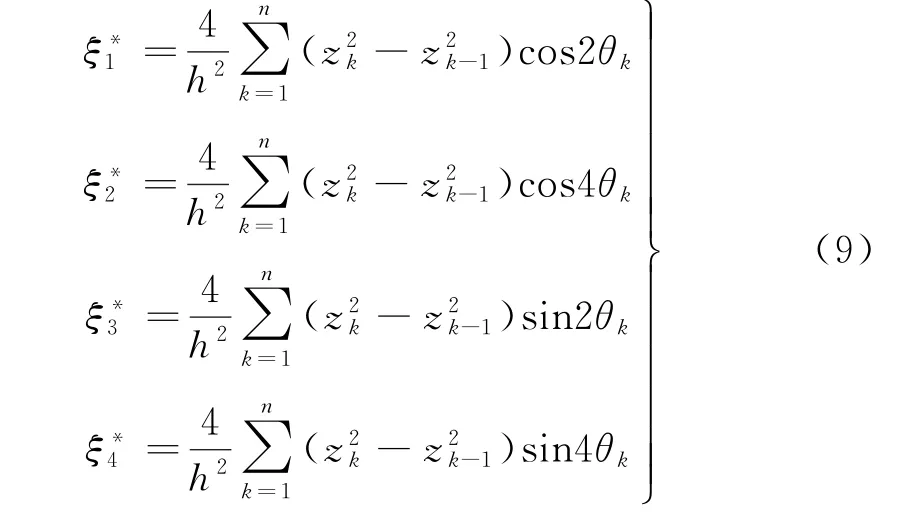
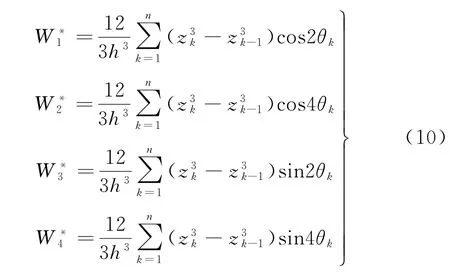
从式(8)~(10)可以看出:
①面内刚度系数V*i仅与层合板的厚度、铺层角度和铺层比例相关,与铺层顺序没有关系,面内刚度系数代表层合板的面内性能。
②耦合刚度系数ξ*i和弯曲刚度系数W*i不仅与层合板的厚度和铺层百分比有关,而且与铺层顺序有关。一个特定铺层的层合板具有唯一的面内刚度系数、弯曲刚度系数和耦合刚度系数。
③当铺层角θ局限在0°、90°、45°和-45°四种铺层角度时,sin4θ=0,所以V*4=ξ*4=W*4=0,此时仅有9个层合系数来表征层合板;当铺层角θ等于0°和90°时,sin2θ=0,由式(10)可以看出W*3仅与45°和-45°铺层的厚度及其铺层位置有关,而且随着45°和-45°铺层距离越近及层合板厚度越厚,W*3越小,因此对层数较多的均衡对称层合板可将W*3作为0处理。
④面内刚度系数V*i和弯曲刚度系数W*i是铺层角位置的奇函数,而耦合参数是铺层角位置的偶函数,所以当层合板为对称铺层时,耦合参数均为0,不为零的可变参数仅为面内刚度系数和弯曲刚度系数。
3 工字型加筋壁板有限元模型
工字型加筋壁板由于稳定性好,被广泛应用于机翼蒙皮、加筋圆筒等结构中。近几年来,开展了很多以减重为目的的工字型加筋壁板优化设计,优化方法也很多,但是大多数方法由于没有充分考虑工字型筋条铺设特点,优化结果不能直接应用于工程实际。本研究充分考虑工字型筋条铺设特点,提出了一种针对工字型加筋壁板的有限元建模方法。
工字型加筋结构的铺设简图如图1所示。从图可见,工字型筋条在铺设中呈C 形铺设,主要包括三个基本层合板:[形腹板、凸缘顶板和凸缘底板。如果按照上凸缘、下凸缘和腹板3个层合板进行优化设计则不能完全反映实际铺层方式,其结果无法直接应用于工程实际中。因此有必要针对工字型筋条的铺设特点,设计建模方法。现根据工字型加筋壁板铺设特点,将工字型加筋壁板简化分为凸缘顶板、[形腹板、凸缘底板、以及基本蒙皮四个层合板,有限元模型的简图如图1(b)。该建模方式考虑了工字型筋条的铺设方式,根据该模型所得的优化结果可以直接用于实际结构的设计。
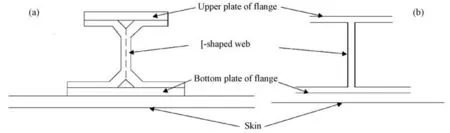
图1 工字型筋条铺设构型及简化模型 (a)铺设构型;(b)简化模型Fig.1 Layup configuration and Simplified model of reinforced panel with I-stiffener (a)Layup configuration;(b)Simplified model
设某一工字型复合材料加筋壁板长700mm,宽为670mm,筋条之间的距离为200mm。加筋壁板的初始几何外形尺寸如图2所示,材料为T300/QY8911。

图2 工字型筋条的几何尺寸Fig.2 Size of I-shaped stiffener
有限元模型采用CQUAD4单元,通过PSHELL属性卡定义各层合板的属性:薄膜材料和弯曲材料。凸缘顶板和上腹板单元采用共节点的双层单元模拟,二者之间的位置关系通过板单元的偏置来实现,凸缘底板和下腹板同样采取共节点的双层单元实现。模型的材料采用等效刚度模型,将面内刚度系数、弯曲刚度系数等加入材料的参数定义中。
加筋壁板的边界为四边简支,X 方向均布轴压载荷,轴压载荷为4746N/mm。具体约束如下:
蒙皮固定端:u=v=w=θx=θz=0
筋条固定端:u=v=w=θx=0
蒙皮加载端:v=w=θx=θz=0
筋条加载端:v=w=θx=0
壁板侧边:w=θy=θz=0
有限元模型及其边界条件如图3所示。

图3 工字型加筋壁板的有限元模型及边界条件Fig.3 Finite element model and boundary condition of reinforced panel
4 加筋壁板二级优化方法
4.1 优化设计方法
层合板的铺层优化采用两级优化策略:第一级优化确定层合板的铺层厚度、铺层百分比和弯曲刚度系数;第二级优化则是以最优弯曲刚度系数和为目标函数进行铺层顺序的设计。
第一级优化一般为连续变量优化问题,采用优化准则法或规划法(NLPQL)。在第一级优化中,工字型加筋壁板的优化设计主要包含4个层合板,分别为蒙皮A、凸缘底板B、凸缘顶板C和[形腹板D,每个层板包括7个设计变量,则总共有28个变量,如表1所示。目标函数是整体加筋壁板重量最轻。约束条件包括强度、刚度、稳定性、铺层比例约束等。局部屈曲载荷系数大于0.67,整体屈曲载荷系数大于1.0,最大轴向应变不大于4000με,最大位移小于1.5mm,而且弯曲刚度系数在设计空间内。

表1 工字型加筋壁板的一级优化设计变量Table 1 Design variable of first level optimization

式中,θi是层合板的铺层角,一般由0°,±45°和90°四种标准铺层角度组成。作者根据Srinvivas和徐小平等[18,19]自适应算法的优点给出了一种改进的自适应遗传算法,通过自编Matlab程序实现,大量对比算例证明,本文提出的自适应遗传算法具有良好的稳健性和收敛性。
4.2 优化结果
经过优化计算,第一级优化设计的结果如表2所示。从表中可以看出,复合材料工字型加筋壁板蒙皮主要采用0°和±45°铺层,凸缘底板和凸缘顶板以0°铺层为主,而[形腹板则以±45°铺层为主。
一级优化采用的层合板厚度为实数,由于单层板为确定值,t=0.125mm,因此需要对各个层合板厚度进行圆整,圆整后各层合板的厚度如表3所示。由于在优化中设置45°和-45°铺层厚度相等,优化得到的层合板为均衡层合板。由于未对层合板的对称性进行特殊处理,所以层合板不一定是对称的。
根据表3中各层合板的层数,以各层合板的弯曲刚度系数为目标,进行铺层顺序优化设计,对优化后的铺层顺序重新计算了弯曲刚度系数,列于表4。从表中可以看到:①铺层为均衡非对称层合板,均衡非对称层合板可以提高结果的稳定性。②通过铺层顺序优化可以找到与一级优化几乎一致的弯曲刚度参数,该二级优化方法是切实可行的。
优化前后的结果如表5所示。从表中可以看出,与优化前相比,工字型加筋壁板的稳定性和最大应变值均有增加,但重量减少了13.13%。工字型加筋壁板优化后的整体失稳图和局部失稳如图4和图5 所示。优化后加筋壁板的局部稳定性略有提高,而整体稳定性则明显下降。主要原因是因为优化提高了蒙皮的局部刚度,但是由于结构重量的明显降低,充分发挥了材料的应用潜力,对结构承载能力有一定的影响。

表2 工字型加筋壁板一级优化结果 Table 2 Results of first level optimization

表3 圆整后的铺层厚度和铺层层数 Table 3 Thickness and layer of laminates after rounding number

表4 工字型加筋壁板的铺层顺序优化结果 Table 4 Result of layup sequence optimization of reinforced panel

表5 约束条件和目标函数优化前后结果对比Table 5 Constraints and object before and after optimization

图4 工字型加筋壁板的整体屈曲模态图Fig.4 Global buckling mode

图5 工字型加筋壁板的局部屈曲模态图Fig.5 Local buckling mode
5 结 论
根据复合材料工字型筋条的铺设特点,本文提出了一种特殊的建模方法,并采用二级优化策略对工字型加筋壁板进行了以强度、刚度和稳定性为约束的轻量化设计,通过本文的研究工作得到如下结论:
1.针对工字型加筋壁板的铺层特点,有限元建模过程中将加筋壁板简化为[形腹板、凸缘顶板、凸缘底板和蒙皮四个层合板,充分考虑了筋条的加工工艺,所得到的优化设计结果可以直接应用于复合材料加筋壁板的制造中。
2.采用二级优化策略开展复合材料加筋壁板的优化设计,可有效解决变量多、铺层角度离散等问题。利用自适应遗传算法提高优化算法的收敛性和稳健性,从而能找到与弯曲刚度系数最为接近的铺层顺序。
