浅谈在课堂教学中学生思维能力的培养
2019-01-30北京市房山区良乡第三中学刘洪辉
北京市房山区良乡第三中学 刘洪辉
一、创设问题情境,激发学生兴趣,引发学生思考
思维发自问题,没有疑难问题向学生提出,学生的思维训练便会落空。教师需精心设置问题情境,设计的问题源于学生已有知识经验,形成教学内容与学生心理需求不协调,欲言又不能完全表达清楚的问题;或是源于生活实际或源于历史典故,需要学生经历探索学习新知后方能回答的问题。例如,《用数观点该看一元二次方程》一课,教师首先引导学生回顾学过的具体函数及方程,然后提出“怎样用函数观点看方程2x+1=x呢?”此问题设计两个要点,一个是函数,另一个是方程,将二者建立联系,从一个新的角度来看方程。此问题的设计促使学生多角度、全面的看待问题,建立知识体系。
学习勾股定理内容时,一位老师是这样设计的:“同学们,今天老师将带领同学们去认识一个人和他发现的一件事,这个人就是古希腊著名的哲学家、数学家、天文学家毕达哥拉斯。相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。同学们,我们也来观察下图中的地面,看看能发现些什么?
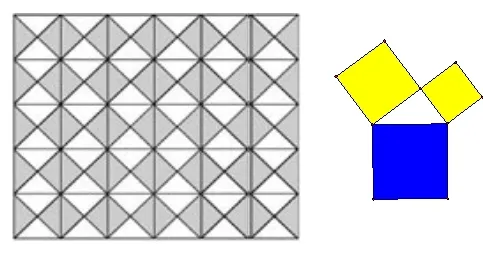
让学生体会数学家研究问题的方法,对孩子们学好本节课知识是一种精神上的鼓舞,激发了学生学习勾股定理的兴趣,为后面新知的学习奠定了基础。
二、展示思维过程, 进行有序思考,培养发散思维
在教学过程中,教师要相信学生,强硬塞给学生的东西远不如学生自己悟出来的深刻。舍得给学生思考问题、探究问题的时间和机会,这样才能暴露学生的错误和闪光点,使教师的教更有针对性。
例如,怎样用函数观点看方程2x+1=x?有学生回答可以看成“求函数y=2x+1和函数y=x的交点横坐标。”“为什么可以这样看呢?”学生感觉有些困难,教师紧紧抓住函数的本质特征—对应与变化的思想进行点拨,引导学生观察方程左右两侧2x+1和x均为x的函数,所以可以看成函数y=2x+1和函数y=x;然后从函数的表现形式解析法和图象法作为突破口,从数和形的角度加以引导分析,若根据等式基本性质将已知方程进行变形还可以有多种看法,类比前面的方法学生很轻松的解决了用函数观点看一元二次方程的问题。教师在教学中应成为“问题者”,凡是学生能解决的问题,就放手让学生去解决,要重视追问学生,使学生知其然还知其所以然,督促学生思考,培养严谨认真的思维习惯。
又如在《角平分线的应用》一课中的问题
例1. 已知:如图,在ABCD中,AD平分∠BAC,AC>AB
求证:(1) ∠B>∠C
(2)若∠B=2∠C 试猜想AC、AB、BD之间的数量关系,并说明理由.
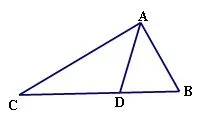
分析:(1)从已知条件看,出现角平分线,就会联想到与角平分线有关的知识,首先考虑到角平分线的定义,会出两角相等;角平分线的性质,会由角平线上的点向叫两边做垂线段;由角的对称性又会联想到翻折,具体操作截长补短,以及有关角平分线的一些基本图形,基本方法等。再结合结论分析欲证两角不等关系,在初中阶段的性质定理中只有一个,就是三角形的一个外角大于与它不相邻的任何一个内角,将结论与已知结合起来分析,思路自通。面对新的问题,教师要逐步培养学生找准主要的已知条件,结合条件展开联想,形成知识串,由已知想可知;再从结论出发,想需知,找到知识的交汇处,问题便可得到解决。好的数学教学,应该是从学生的生活经验和已有知识经验出发,提供给他们充分进行数学实践和交流的机会,是他们真正掌握数学知识、思想和方法,同时获得广泛的数学活动经验 。
三、重视归纳、总结、提升,促使学生抓住问题的本质,提高思维的深刻性
问题的本质,不单指定义,定理,公式,还有知识间内在的联系与规律。因此数学教学不能就题论题,学生停留在反复做题之中,而是着眼于知识系统,通过有选择的做题,适时的引导学生归纳概括总结,加强反思,从特殊到一般,从方法到规律,抓住问题的本质,能够做到举一反三,融会贯通,从而培养学生思维的敏锐性,加深学生对知识的深刻理解。如《用函数观点看一元二次方程》一课,学生经历探究用函数观点看一元一次方程、一元二次方程的过程,积累了一定经验,通过回顾反思,进行概括总结,得出如下结论:从函数角度来看方程,可以从数和形两个方面来进行描述,总的归纳起来有两种各看法:一种看法,从数看一个方程可以看成求一个函数当函数值为零时对应的x的值 ,从形看是求该函数图象与x轴交点的横坐标;另一种看法:从数看可以看成是求两个函数在函数值相等时对应的x的值,从形看是求这两个函数图象与x轴交点的横坐标。概括是思维的基础,随着概括水平的提高,学生的思维从具体形象思维向抽象逻辑思维发展。数学教学中,教师需不断的向学生提出高一级的概括任务,已逐步发展学生的概括能力。
总之,教师需认真备课,精心设计课堂内容,从教材中挖掘有助于开发学生思维的素材,创设问题情境,引起认知冲突,追根溯源,将培养、发展学生的思维能力作为核心内容,有助于培养学生创新意识、严谨的思维习惯以及实事求是的做人态度,有助于学生建立知识网络及学生综合素质的提高。
