绝缘材料的介质损耗角在线检测方法研究
2019-01-30,,,
,,,
(湖南工业大学 电气与信息工程学院,湖南 株洲 412000)
0 引言
介质损耗角是反应绝缘材料损耗状况的重要特征参数[1-2]。通过对介质损耗角的检测,并进行数据分析可以实现故障的诊断。如何在复杂工况下提高损耗角检测的可靠性是学者们研究的重点内容。
现有损耗角的检测方法中,有的基于硬件实现[3-4]如:过零点相位监测、相位法等,误差较大且易累积,增加了硬件实现的复杂程度。有的基于软件实现[5-7]如:谐波分析法,相关分析法,高阶正弦拟合方法等,软件实现降低了硬件成本,数据处理的实时性和可靠性较高。谐波分析法数字化实现简单,并且三角函数的正交性具有一定的抗干扰能力,因此被广泛应用。但是采用谐波分析法时由于电源信号频率的波动以及环境中的大量谐波干扰,频谱泄露和栅栏效应是影响测量误差的重要因素[8]。即使在硬件电路设计时加入锁相环也无法实现严格的信号同步采样。文献[9-10]提出了几种提出了几种减少栅栏效应和频谱泄漏的新算法,如加窗插值算法,传统相位差较正算法等。一些经典的窗函数如:hanning窗、Blackman-Harris窗、Nuttall窗等被应用,为追求更优良的窗函数性能,又提出了卷积窗[11]来抑制频谱泄露。在考虑谐波和噪声的干扰,插值算法和相位差校正算法中相位失真较为严重。同时插值算法在求解过程中需要进行多项式的拟合,计算量大对处理的实时性有一定的影响。
本文通过比较不同窗函数的性能,选择旁瓣较小,且无负值,衰减较快的三角窗进行卷积来抑制频谱泄露。同时对全相位数据预处理方法进行研究,提出可以应用到实际工程的相位校正算法,且计算量较小。通过仿真结果表明,本文采用的算法测量误差较低,具有较高的可靠性。
1 介质损耗角在线检测原理
绝缘材料长时间工作在复杂的工况下,由于电导和极化的滞后作用会使内部介质损耗,引起绝缘温度的上升导致绝缘材料烧焦,从而失去绝缘性能。通过检测介损角因素来反应绝缘材料损耗情况。
对于电容型绝缘材料来说,可以将其等效为电容和线性电阻的并联组成,结构如图1所示。

图1 绝缘材料失效机制
理想的绝缘材料,按照电容效应,电流超前电压90度。设等效电路功率因素角为φ,则介损角可表示为δ=90°-φ。一般情况下Ic远大于Ir,因此介损角很小,一般为0.001~0.02 rad,不容易被检测。根据电流模型可得:
tanδ=tan(90°-φ)=tan(90-(φi-φu))
(1)
式中,φi为泄露电流初始相位角;φu为绝缘材料两端电压初始相位角。
介质损耗角在线检测设备安装于被测绝缘材料处,在交流电源的作用下,利用传感器实时同步采集通过绝缘材料的泄露电流和两端电压数据,对检测信号进行调理后送入处理器计算等效电路中电压和电流的初始相位角,带入式(1)即可计算介质损耗角。在线检测原理如图2所示。但是被检测绝缘设备在运行时信号的检测会受到各种干扰,初始相位角的计算往往存在较大的误差。因此需要对相位角高精度计算方法进行研究。
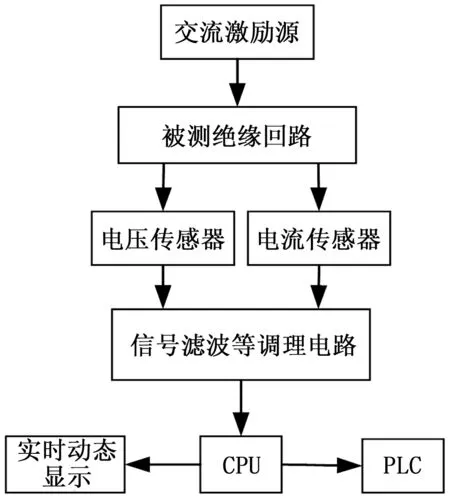
图2 介损角在线监测实现原理图
2 三角自卷积窗(TSCW)
2.1 三角窗函数及频谱
窗长为N的三角窗离散时域函数可以表示为:
(2)
为了便于三角窗FFT的数字化实现,通常选取:
N=2i(i=1,2,3,4…)。设采样周期为Ts,则三角窗的频谱函数为:
(3)
式中,w=2π/Ts。三角窗的主瓣宽度为8π/N,旁瓣峰值电平-27 db,旁瓣衰减率12 db,相对于其他经典窗函数,实现简单,同时频谱无负瓣,有较高的旁瓣衰减率,因此本文选择三角窗作为卷积窗的母窗。
2.2 TSCW频谱分析
根据卷积窗的定义:TSCW在时域可以看做是窗宽为N的P个三角窗的做P-1次时域卷积,可表达成下式:
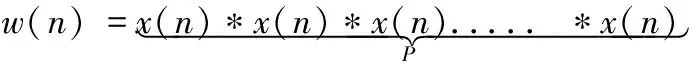
(4)
由卷积的性质,TSCW的频谱函数为三角窗在频域的乘积,因此TSCW的频谱函数为:
(5)
TSCW的窗宽为PM-P+1,对序列补充P+1个0可以得到宽度为PM的窗口。对连续的IDFT频谱进行离散化,频率间隔即分辨率为w=2kπ/M(k=0,1...M-1),M=PN为卷积窗宽。因此可以将式(5)改写为:
(6)
从(6)式可以看出,使得|w(k)|=0充要条件是:
(7)
当k=2pd时,满足|w(k)|=0。对于频谱图最靠近原点右侧的零点为处k=2p,与零点的频谱距离为4pπ/M,因此长度为N的三角窗进行P阶卷积后的频谱函数主瓣宽度为:
(8)
从式(8)可以看出,TSCW的主瓣宽度与母窗长度成反比关系。根据M=PN,当TSCW的宽度固定时,卷积的阶数和母窗长度成反比。因此对于宽度为M的TSCW,随着卷积阶数的增加,主瓣越宽。
选择窗长度为N=128的三角窗为母窗进行卷积与N=128经典窗函数进行频谱特性对比分析。图3给出了1~4阶TSCW的傅里叶变换幅频曲线,同时标注了各响应的旁瓣峰值电平。可以看出随着卷积阶数的增加,卷积窗的峰值旁瓣电平和旁瓣滚转率等旁瓣性能迅速加强。表1给出了一些经典窗与不同阶数的TSCW的频谱特征值。这意味着选择合适的卷积阶数的TSCW对采集信号进行截断,可以有效的抑制频谱泄露,提高相位角的计算可靠性。
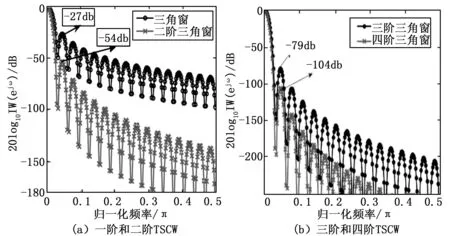
图3 一阶至四阶三角卷积窗频谱图

窗函数主瓣宽度旁瓣峰值(db)旁瓣衰减率(db)hanning8π/N-3118hamming8π/N-436blackman12π/N-5918三角窗8π/N-27122rd-TSCW16π/N-52243rd-TSCW24π/N-79364rd-TSCW32π/N-10448
综合以上分析,TSCW具有较好的旁瓣峰值电平和衰减率,可以有效地抑制频谱泄漏,但是随着卷积阶数的增加处理器对数据的计算量也增加,本文选择二阶TSCW来进行介损角的测量。
3 全相位相位角检测
3.1 全相位(apFFT)介绍
apFFT数据预处理[12]对采样的2N-1个数据,通过加窗(单窗,双窗,无窗),然后应用叠加运算进行FFT运算。利用了傅里叶变换的线性时不变性,较大的提高了频谱和相位谱分析的准确度。全相位数据预处理过程如图4所示。
图中,w(n)为前窗f和翻转后窗b的卷积,其长度均为N,表达式为:
w(n)=f(n)*b(-n)
(9)
当f(n)=b(n)=Rn(矩形窗)时,称为无窗全相位;当f(n)与b(n)中任意一个不是Rn时,称为单窗全相位;当f(n)=b(n)≠Rn时,称为双窗全相位。
3.2 性能分析
输入信号为给定单一频率的复指数序列:
x(n)=Aejwn+φ
(10)
式中,w为信号频率,A为信号幅值,φ为信号相位角。
传统的傅里叶变换,由于信号频率的波动,以及采样时对信号的截断,使得分析存在着严重的频谱泄露和栅栏效应,这会对相位角的计算造成较大的误差。
对式(10)进行傅里叶变换时,设采样频率固定,当信号中频率出现波动时,采样频率非信号频率的整数倍,会出现非同步采样。频谱图如图5所示。

图5 传统FFT频谱
从图4可以看出,当信号频率出波动时,频谱分析相对于同步采样出现较丰富的旁瓣,频谱泄露严重,峰值谱线不能很好的集中有用信号。信号的幅值、频率和相位角都会出现较大的误差。同时对信号进行DFT运算有:
(11)
从式(11)得到传统DFT相位误差值式(12),可以看出,相位角的误差也随频率变化相关。
(12)
apFFT数据预处理过程如下:
1)用窗f对截断数据xi进行加窗;
2)加窗后的xi进行周期延拓;
3)用后窗b对向量相同位置加权叠加求和;
4)最后得到的向量进行FFT运算;
对式(10)信号分别进行apFFT频谱响应Y(k)与传统的傅里叶变换频谱响应X(k)分析,它们之间加窗后存在一定的关系如式(13)所示。
Y(k)=|X(k)|2ejφ=|W(kΔw-w*)|2ejφ
(13)
式中,W(w)为所加窗函数的频谱函数。可以看出,加窗后的apFFT的幅值为传统傅里叶变换幅值的平方,使得apFFT主谱线幅值更加集中,旁瓣的幅值谱线也按照平方的速度衰减,所以apFFT可以很的抑制频谱泄露,同时相位角不会受到影响,提高了介质损耗角检测中相位角计算的可靠性。
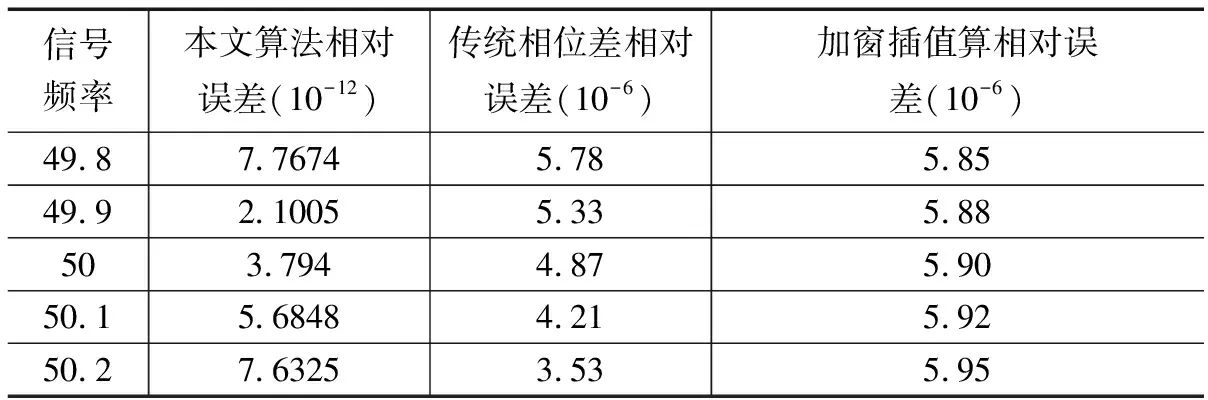
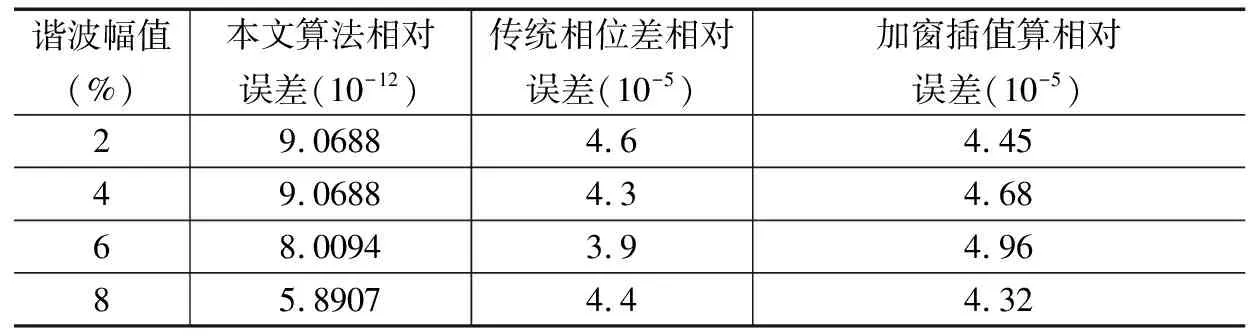
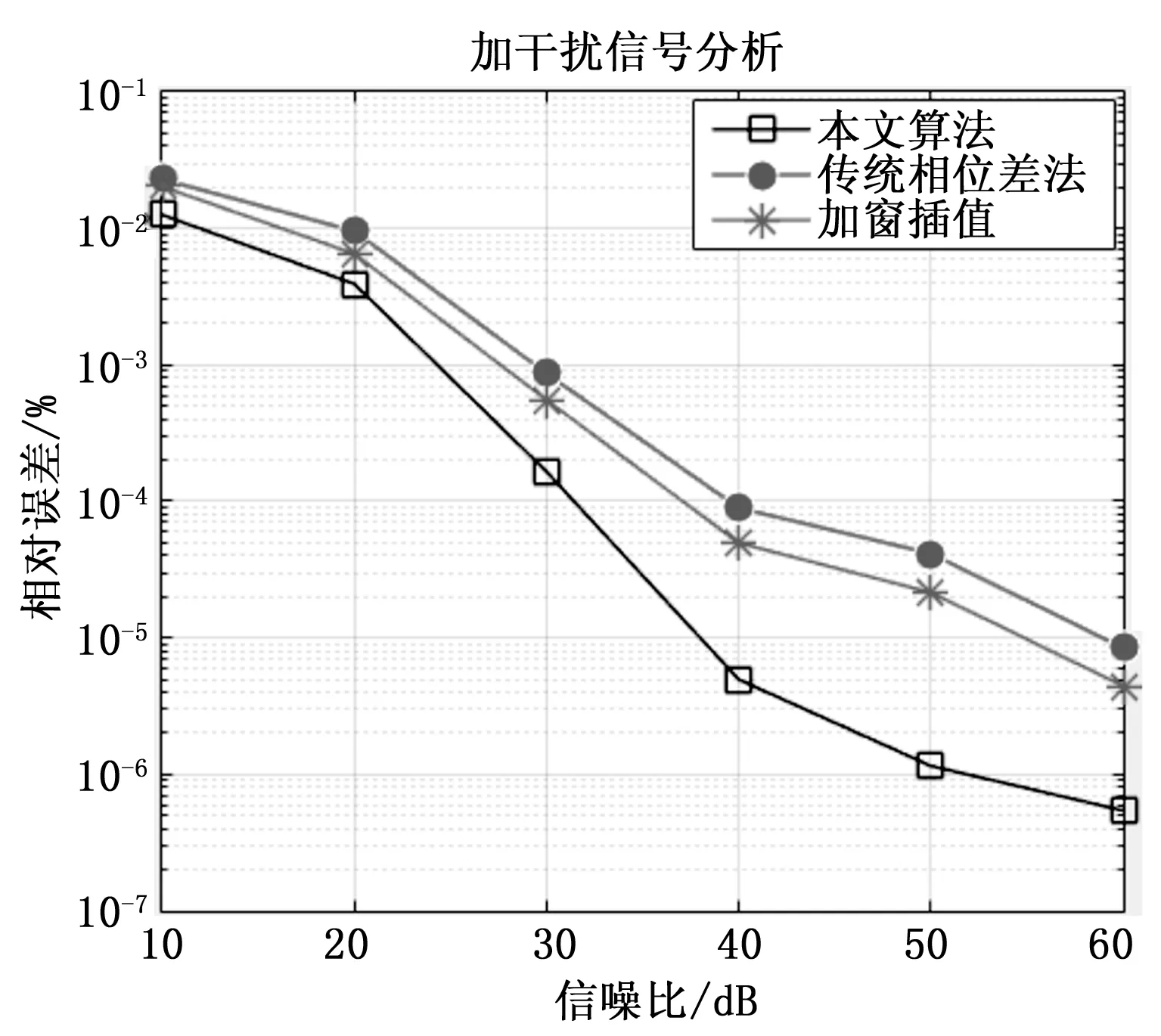
假设给定信号s同时包含多种信号频率和初始相位值,信号频率非整数容易出现非同步采样,s=10*cos(10.2*2*pi*t/256+pi/10)+2*cos(20.8*2*pi*t/256+pi/3)+2*cos(30.1*2*pi*t/256+pi/3)+2*cos(40.5*2*pi*t/256+pi)(-N+1 图5 传统加窗与apFFT分析对比图 通过仿真,看到传统加窗FFT旁瓣较为多,而apFFT的旁瓣明显减弱很多,主要集中在峰值谱线两侧相邻的谱线中,这对式(13)也是一个很好的验证。因此apFFT对于抑制频谱泄露有着更好的效果。但是由于栅栏效应的存在,apFFT的频率点和信号实际的频率存在较小的误差,同时apFFT中,信号频率点处所对应的相位谱的相位值与信号中心样点的实际相位值保持一致,即‘相位不变性’。 相对于传统FFT算法复乘N2及N(N-1)的运算量,apFFT的运算量仅在此基础上增加了N次累加运算,增加较少的运算量却可以得到较大的性能改善。 apFFT频谱分析具有抑制频谱泄露、‘相位不变性’的特点,但是在理论推导过程中数据的截断是取以x(0)为中心前后2N-1个数据进行分析,所得到的相位值为信号在x(0)处的相位值。在实际的工程应用中,无法对x(0)前的数据截取,因此只能取x(0)的后2N-1个数据。这时采样中心点发生变化,因此apFFT计算得到的相位角不是初始相位角,需要对结果进行校正。 针对上述问题,取前2N-1个数据进行全相位数据预处理,此时通过FFT得到的相位谱为频率点处的相位值为第N个数据的相位值φ1;然后将数据进行延时L后进行全相位预处理后得到的相位位第N+L个点的相位值φ2。 (14) 由于φ1,φ2的取值范围均为[-π,π]。如果以φ1为标准,与数据延时L后得到的φ2的值较大时Δφ=[-2π,2π],就会出现‘相位模糊’,一值多解。因此本文中取L=1,当频率不是很大时可以保证Δφ=[-π,π]。同时由于时移在相位谱中有附加相移2kLπ/N,相位差理论值与实际值之间存在如下关系: Δφ*=Δφ+2kLπ/N (15) 当采样数据N值很大时为了计算简便,附加相移可以忽略不计。利用相位差很容易推导出信号初始相位的估算方法: w0=Δφ (16) θ0=θ1-NΔφ (17) 上式即为最后的相位校正公式。相关校正流程可以用图6表示。 图7 相位角流程图 为了验证本文所提算法的有效性,选择文献[10]所提的传统相位差校正算法及文献[11]加窗插值算法进行对比。在仿真电路中模拟绝缘材料等效电路参数,设置电阻值R=22.67 kΩ,电感为591.2 nF,采样频率为2.5 kHz,电源频率为50 Hz,介损角的理论值0.004 129。仿真中考虑更多的实际因素对测量结果的影响,如:信号频率波动、谐波干扰、噪声的干扰等。 选择N=256,构建二阶TSCW。电压信号的频率波动范围为48.2~50.2,分别得到三种不同检测方法的相对误差值如表2。 表2 信号频率波动引起的介损角相对误差 通过分析可以看出,在频率波动的情况下,传统的相位差法与加窗插值算法计算得到的介损角值误差相差不是很大,本文通过提出的加TSCW窗的apFFT相位校正算法法,介损角的检测可以达到10-12精度值,采集较小的数据长度进行较少的运算量,可有有效的克服基波频率波动对检测结果的影响。 在非同步采样时,由于频谱的泄露,谐波的注入会对计算结果产生较大的影响。取电源基波信号频率为f=49.8,在电源信号中加入不同比例的三次谐波,幅值分别为2%~8%,并且与文献[10]方法进行对比。进行仿真分析后得到表3。 表3 谐波简谐波引起的介损角相对误差 由以上可以得到加TSCW窗的apFFT可以有效的克服谐波对测量结果的影响。在谐波干扰下,测量结果稳定并且精度较高。 加入不同程度的噪声干扰,对比不同算法的检测误差,通过仿真得到图8的结果。三种方法中当信噪比大于30 dB时,本文算法可以达到较高的精度;但当信噪比低于30 dB,三种方法相对误差相差不是很多。 -N≤n≤N-1 图8 加干扰后相对误差曲线 综上所示,与传统方法相位差校正算法及加窗插值算法,appFFT在频率波动、谐波干扰、噪声干扰的情况下能有有效的抑制频谱泄露和栅栏效应,可以保证介质损耗角较高的测量精度。 本文讨论了一种新的介质损耗角在线检测的数字算法,所提出的方法中将卷积窗的优良特性结合全相位数据处理算法应用于介质损耗角的检测,并改进相位角校正算法。仿真研究表明,相对于传统的相位差算法及加窗插值算法,该算法在较小的数据处理量下,可以较好的保证测量的精度,提高绝缘性能检测的可靠性。
3.3 相位谱校正方法改进
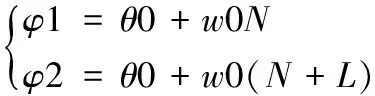

4 仿真研究
4.1 信号频率波动测量结果的影响的分析
4.2 谐波干扰对测量结果的影响
4.3 加入白噪声对测量结果的影响
5 结论
