高超声速飞行器平稳滑翔弹道扰动运动伴随分析

2019-01-30赫泰龙陈万春刘芳

北京航空航天大学学报 2019年1期

赫泰龙，陈万春,*，刘芳

(1. 北京航空航天大学宇航学院, 北京 100083； 2. 北京航天长征飞行器研究所，北京 100076)

高超声速飞行器，相比于传统弹道式飞行器，具有远距离快速打击、覆盖范围广、全过程机动能力强、弹道难以被预报等优点，被认为是突破目前防空反导系统的有效手段，在军事上有广阔的应用前景。高超声速飞行器无动力滑翔段弹道设计是当前研究热点方向之一，平衡滑翔是再入的一种重要飞行模式，最早由德国科学家Sänger和Bredt[1]提出，平衡滑翔弹道高度变化平缓、热流密度和动压峰值小，被广泛应用于再入弹道的分析与设计[1-2]。胡锦川和陈万春[3]在传统平衡滑翔概念的基础上，通过分析给定攻角曲线和倾侧角曲线再入弹道族的特点，以纵向加速度导数的平方的积分来衡量弹道的平滑程度，提出了平稳滑翔弹道概念，并对平稳滑翔弹道的解析解和弹道动态特性进行了分析，获得了快速生成平稳滑翔弹道的方法[4]。平稳滑翔弹道是本文主要研究对象。

对于高超声速滑翔弹道扰动运动的分析，通常采用非线性仿真方法[3-4]，针对不同的干扰因素和不同参数(剩余飞行时间等)，需要分别进行多次仿真；而对于随机扰动，则需要大量的蒙特卡罗仿真，计算效率低，但是方法简单，适用条件广。在小扰动假设下，对平稳滑翔动态方程线性化，利用伴随仿真方法分析，可以大大减少计算量。

伴随仿真方法是一种计算机仿真分析与设计工具，主要用于分析线性时变系统[5-6]。伴随仿真方法的理论基础是线性系统与其伴随系统之间的本质关系(内积等式)[7]，一般的线性时变系统可以采用2种方法来描述：状态空间法和脉冲响应矩阵。所以，关于伴随仿真方法的解释也可以分为基于状态空间描述(状态转移矩阵)[8-9]和基于脉冲响应矩阵[5-6]。伴随系统一次仿真可以得到原线性系统各不同干扰输入对某一输出的影响，通常称为误差预算或灵敏度分析，在电路网络分析中有广泛应用。伴随仿真另一个重要性质是一次仿真可以得到原线性系统在各干扰输入不同的加入时间下某一特定时间(如仿真终端时刻)的输出，该性质广泛应用于导弹制导回路的分析与设计中[6]。伴随仿真方法还可以用于分析输入为随机过程(如白噪声信号)的线性系统的均方响应，本质上可以理解为线性系统协方差分析[5-6]的伴随仿真方法。Zarchan[10]基于伴随仿真方法，提出了用于分析非线性导弹制导系统的统计线性化伴随仿真方法(SLAM)。Weiss和Bucco[11]用伴随仿真方法对战术导弹的交班进行了分析，并对如何在非标准输入信号的制导系统应用伴随仿真方法进行了研究[12]。Bucco[13]还系统地介绍了伴随仿真方法在航空航天领域的应用。Sarachik和Kreindler[14]、Brogan[15]、Zarchan[6]、Weiss和Bucco[16]分别研究了离散系统、连续-离散(混成)系统的伴随仿真方法。林晓辉、崔乃刚和刘暾[17]对伴随理论有关定理用于随机运动体仿真技术作了研究。邹晖、陈万春和邢晓岚[18]基于MATRIXx开发出了能够自动生成原系统的伴随系统的工具软件。伴随仿真方法在摄动制导方法的分析与设计中也有重要应用[19-20]。

本文利用伴随仿真方法，研究状态初值和气动力等存在扰动因素(包括确定性常值小扰动和随机扰动)时，对平稳滑翔弹道终端高度、速度和射程的影响。首先，从伴随系统基本定义出发，给出了伴随仿真方法统一的解释。在滑翔动力学建模和平稳滑翔弹道定义基础上，研究了平稳滑翔弹道的基本性质。考虑扰动因素，建立带有误差干扰的非线性动力学模型，并根据小偏差弹道摄动理论，在标准平稳滑翔弹道附近线性化，得到关于扰动运动的线性化微分方程。然后，采用伴随仿真方法，同时对比非线性仿真和蒙特卡罗法，分析了各扰动因素对平稳滑翔弹道的影响；针对平稳滑翔弹道存在初始高度、初始弹道倾角、初始速度及升力、阻力等多个扰动因素，伴随仿真方法只需要一次仿真就可以得到各扰动在不同剩余飞行时间加入时对终端高度、终端速度或终端射程的影响，而非线性仿真需要分别对每个扰动进行仿真、对加入扰动时剩余飞行时间进行循环，而且对于随机扰动则需要进行大量蒙特卡罗打靶，所以伴随仿真方法的计算量要远小于非线性仿真或蒙特卡罗仿真。研究结果有利于加深对高超声速飞行器平稳滑翔弹道特性的认识，并能为基于平稳滑翔弹道的制导方法设计分析及仿真评估提供参考。

1 伴随仿真方法

为了阐述伴随仿真方法的原理，本节从线性时变系统的伴随系统的定义出发，利用线性系统与其伴随系统之间的本质关系(定义式)，给出伴随仿真方法的统一解释。

〈Gu,ν〉Y=〈u,G*ν〉U∀u∈U,∀ν∈Y

(1)

式中：〈·,·〉为空间U或Y上的内积。

1.1 伴随系统状态空间表示

考虑如下状态空间描述的线性时变系统：

(2)

式中：u(t)∈Rm为控制输入；x(t)∈Rn为状态向量；y(t)∈Rp为输出；A(t)、B(t)和C(t)为关于时间t连续的函数矩阵。

系统式(2)的解可以表示为

(3)

式中：Φ(t,τ)为状态转移矩阵。

假设u∈U，y∈Y，信号空间U和Y都是有限时域勒贝格-2空间；为了考虑初值，将系统式(2)写成如下抽象形式：

(4)

式中：⊕为直和。

定义内积为

(5)

容易验证，Rn⊕U和Rn⊕Y均是希尔伯特空间。利用线性系统伴随的定义式(1)，可以推导出线性系统式(2)的伴随系统。

(6)

存在如下状态空间实现[21]：

(7)

为了验证系统式(7)是式(2)的伴随的状态空间实现，进行如下推导运算：

(-pT(t)A(t)-rT(t)C(t))x(t)+

pT(t)(A(t)x(t)+B(t)u(t))=

-rT(t)C(t)x(t)+pT(t)B(t)u(t)=

-rT(t)y(t)+uT(t)q(t)

对上式从t0到tf积分可得到

pT(tf)x(tf)-pT(t0)x(t0)=

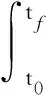
(8)

式(8)对任意x(t0)∈Rn，u∈U，p(tf)∈Rn，r∈Y 都成立。对式(8)左右两边进行简单移项，并结合内积定义式(5)，可以看出式(8)正是伴随系统定义中式(1)的状态空间变量表示，这说明系统式(7)和式(2)互为各自伴随的状态空间实现。式(8)通常称为Bliss公式[19]或伴随定理[17]。

注意到，伴随系统式(7)的时间进程是反向的(从tf到t0)，为了仿真方便，作如下变量替换：

(9)

为了书写方便，不失一般性，后文将假设t0=0。

利用式(7)进行简单求导运算和变量代换，可得到

(10)

式(10)的解为

ν(τ)dτ

(11)

式中：Ψ(t,τ)=ΦT(tf-τ,tf-t)为系统式(10)的状态转移矩阵。如无特别说明，线性系统式(2)的伴随系统是指式(10)，相应地，伴随系统定义式(8)则写为

zT(0)x(tf)-zT(tf)x(0)=

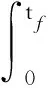
(12)

1.2 伴随仿真统一解释

利用伴随的定义式(12)，能够以更简单、统一的方式来解释伴随系统式(10)的仿真结果与原系统式(2)之间的关系。

注意到，式(12)只显含原系统和伴随系统的初始状态、终端状态、控制输入和输出，且由伴随定义可知式(12)对任意的初始状态x(0)、z(0)，输入u(t)、ν(t)都成立。利用式(12)来解释伴随仿真方法的基本思路是：对原系统和伴随系统选取适当或特殊的状态初值和输入，讨论原系统和伴随系统仿真结果(终端状态、输出)之间的关系。对于具体待研究的线性系统，状态初值和输入都给定，则只需要对伴随系统选取适当或特殊的状态初值和输入。

(13)

式中：f(t)为任意函数。

伴随仿真的基本解释可以概括为如下2条性质。记x=(xk)∈Rn，z=(zk)∈Rn，u=(uk)∈Rm，ν=(νk)∈Rp，y=(yk)∈Rp，w=(wk)∈Rm。

性质1(误差预算) 假设原系统式(2)为多输入-单输出(MISO)，给定任意控制输入u(t)和状态初值x(0)，则可以选取伴随系统式(10)的输入ν(t)=δ(t)，初值z(0)=0；代入式(12)，可得到

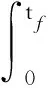
(14)

还可以选取伴随系统ν(t)=0，z(0)=CT(tf)，注意到原系统式(2)为MISO，所以z(0)和CT(tf)是同维数的，利用原系统输出方程y(t)=C(t)x(t)和式(12)，同样可以得到式(14)。

特别地，如果原系统式(2)的u(t)=0，式(14)可写为

(15)

如果原系统式(2)中u(t)的每个分量都是δ(t)，即uk(t)=δ(t)，k=1,2,…,m，则式(14)可记为

(16)

式(14)表明原系统式(2)在终端时刻的输出y(tf)，可以利用伴随系统式(10)的仿真结果得到；而且伴随一次仿真可以得到原系统输入和状态初值各分量对终端输出y(tf)的贡献大小，这一点可以从式(15)、式(16)更清楚地看到。性质1也给出伴随仿真初值和输入的具体选取方法，特别地，对于原系统输入为典型信号的[12]，可先等价转化为零输入、阶跃输入或脉冲输入的线性系统[6]，然后对此系统进行伴随仿真，更方便操作和理解。

性质2(伴随一次仿真的通用解释) 为了简化叙述，不失一般性，这里假设原系统式(2)为单输入-单输出(SISO)，且状态初值x(0)=0，控制输入u(t)=δ(t-(tf-tgo))，tgo∈[0,tf]；选取伴随系统式(10)的ν(t)=δ(t)，z(0)=0或ν(t)=0，z(0)=CT(tf)，代入式(12)可得到

y(tf)=w(tgo)

(17)

式(17)对所有tgo∈[0,tf]成立，这说明原系统在仿真时刻为tf-tgo，或者说在剩余仿真时间为tgo时，加入脉冲输入，得到终端输出y(tf)，等于伴随仿真在tgo时刻输出；为了得到原系统在不同剩余仿真时间时脉冲输入响应，原系统需要按照tgo循环，进行多次仿真，而伴随仿真，因为初值和输入选择给定，只需要一次连续仿真就可以得到所有tgo时刻的输出。

原系统为MISO时，结论类似，还可以得到各输入导致终端输出的误差预算。假设原系统x(0)=0，可以通过增加阶跃输入或脉冲输入转化得到[6]。

1.3 协方差分析的伴随

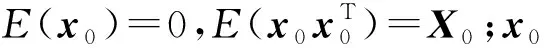
(18)

式中：X(t)=E(x(t)xT(t))；Y(t)=E(y(t)·yT(t))。利用该方程进行仿真分析通常称为协方差分析。协方差矩阵X(t)、Y(t)对角线元素表示各分量的方差(均方)，非对角线元素表示各分量之间的协方差。式(18)是一个矩阵微分方程，如果将X(t)作为状态，U(t)作为输入，Y(t)作为输出，仍是线性时变系统，这可从如下等价系统得到：

(19)

式中：vec(·)表示矩阵拉直运算，即将矩阵按照列的顺序，一列接一列地组成一个长向量；⊗指克罗内克积。显然，系统式(19)就是常见的状态空间描述形式。线性矩阵微分方程式(18)的解为

X(t)=Φ(t,0)X(0)ΦT(t,0)+

(20)

类似式(2)与式(10)的关系，利用式(19)，可以直接得到系统式(18)的伴随系统的一个矩阵微分方程实现为

(21)

系统式(21)微分方程的解为

Z(t)=Ψ(t,0)Z(0)ΨT(t,0)+

(22)

容易证明，系统式(18)与式(21)之间存在类似于式(12)的如下关系：

tr(ZT(0)X(tf))-tr(ZT(tf)X(0))=

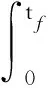
tr(UT(t)W(tf-t)))dt

(23)

式中：tr (·)表示方阵的迹。

系统式(21)可以称为协方差分析式(18)的伴随，利用式(23)能够得到类似于确定性线性系统的性质1、性质2的伴随解释，只不过输入输出换成功率谱密度和协方差矩阵，不但可以分析均方响应(对角线元素)，还可以分析各输入分量之间相关性(非对角线元素)对输出的影响。作为例子，考虑MISO线性系统式(2)的协方差传播微分方程式(18)，给定初值X(0)，输入U(t)；选取伴随系统式(21)的输入V(t)=δ(t)，初值Z(0)=0，或者V(t)=0，Z(0)=CT(tf)C(tf)，代入式(23)可得

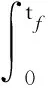
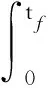
(24)

同时考虑相应的确定性伴随系统式(10)，即如果选取伴随系统式(21)中Z(0)=0，V(t)=δ(t)，同样选取伴随系统式(10)中z(0)=0，ν(t)=δ(t)；如果选取伴随系统式(21)中Z(0)=CT(tf)C(tf)，V(t)=0，同样选取伴随系统式(10)中z(0)=CT(tf)，ν(t)=0。那么，结合式(11)、式(22)，同时利用迹的循环性质，式(24)可写为

Y(tf)=zT(tf)X(0)z(tf)+

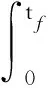
(25)

如果初值x(0)各分量之间不相关，即X(0)的非对角线元素为0；U(t)=I，即u(t)为单位功率谱密度白噪声过程，则有

(26)

至此，利用伴随系统的数学定义式，对确定性线性系统和随机线性系统的伴随仿真给出了统一的解释；单从仿真结果来考虑，这里给出的解释本质上不需要借助于状态转移矩阵或脉冲响应矩阵，形式上也更简单。

2 滑翔动力学模型

考虑地球模型为静止均质圆球，高超声速飞行器纵平面内再入滑翔的受力分析如图1所示。图中：Oexiyi为地心坐标系；Obxgyg为地理坐标系；Obxb为弹体坐标系x轴；h为高度；γ为弹道倾角；s为射程；α为攻角；v为速度；L为升力；D为阻力；g为重力加速度；m为质量；Re为地球半径。

图1 变量符号及受力分析示意图Fig.1 Schematic of variable symbol and force analysis

滑翔动力学微分方程可表示为

(27)

式中：

(28)

其中：ρ为大气密度，通常采用指数大气模型；ρ0=1.225 kg/m3；β=1.389×10-4m-1；g0为海平面重力加速度，取g0=9.806 65 m/s2；S为气动参考面积；CL为升力系数；CD为阻力系数。本文在仿真计算时采用通用航空飞行器CAV-H[22]的相关模型数据，该飞行器质量m=907 kg，气动参考面积S=0.483 9 m2，升力系数和阻力系数关于攻角的拟合公式[3]为

CL=0.046 75α+0.105 68

CD=0.000 508α2+0.004 228α+0.016 1

式中：攻角单位为(°)。

3 平稳滑翔弹道

针对常值攻角控制输入，分析平稳滑翔弹道的性质。按照定义[3]，给定滑翔初始速度v0，以初始弹道倾角γ0和高度h0为优化变量，以式(29)为性能指标，同时满足微分方程约束式(27)，优化得到的弹道称为平稳滑翔弹道。

(29)

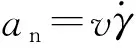
考虑时间常数tc对优化结果的影响，表1列出了选取不同时间常数tc优化得到的初始弹道倾角和初始高度。本算例优化条件是：初始速度v0=7 000 m/s，常值攻角输入α=15°，采用序列二次规划(SQP)方法进行优化。从表1可以看出，不同的时间常数tc得到的优化结果之间相差非常小，从后面分析还将会看到，这些微小差异对整个平稳滑翔弹道的影响也是可以忽略的。基于此，后文仿真计算中，将时间常数固定为tc=1 000 s来获得平稳滑翔弹道。

根据定义，在每一个初始速度都可以通过优化得到对应的平稳滑翔弹道。图2给出了不同初始速度下优化得到的平稳滑翔弹道对比曲线。可以明显看出，平稳滑翔弹道各状态量变化平稳；从图2(e)、(f)还可以得到平稳滑翔弹道另一重要特征，即不同初始速度下优化得到的平稳滑翔弹道高度-速度曲线、弹道倾角-速度曲线几乎重合，或者说初始速度小的平稳滑翔弹道是初始速度大的一部分，以较小的初始速度优化得到平稳滑翔弹道初值是在初始速度大的弹道上，这表明平稳滑翔弹道上任一点状态(h、γ、v)作为初值都满足平稳滑翔弹道的定义，或者说平稳滑翔弹道上的任一段仍然是平稳滑翔弹道，这可以称为平稳滑翔弹道定义的一致性。

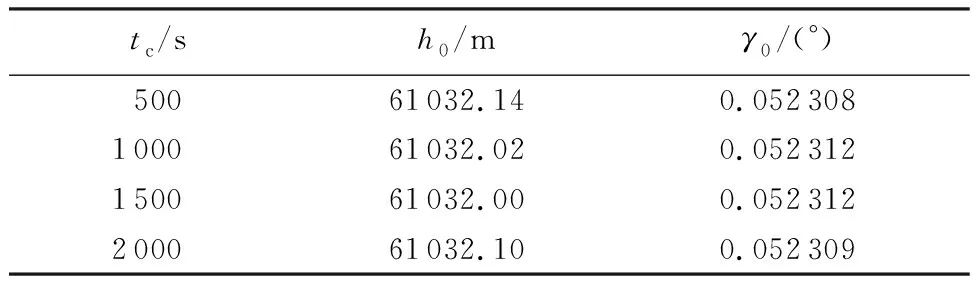
表1 不同时间常数tc的优化结果Table 1 Optimization results with different time constants tc

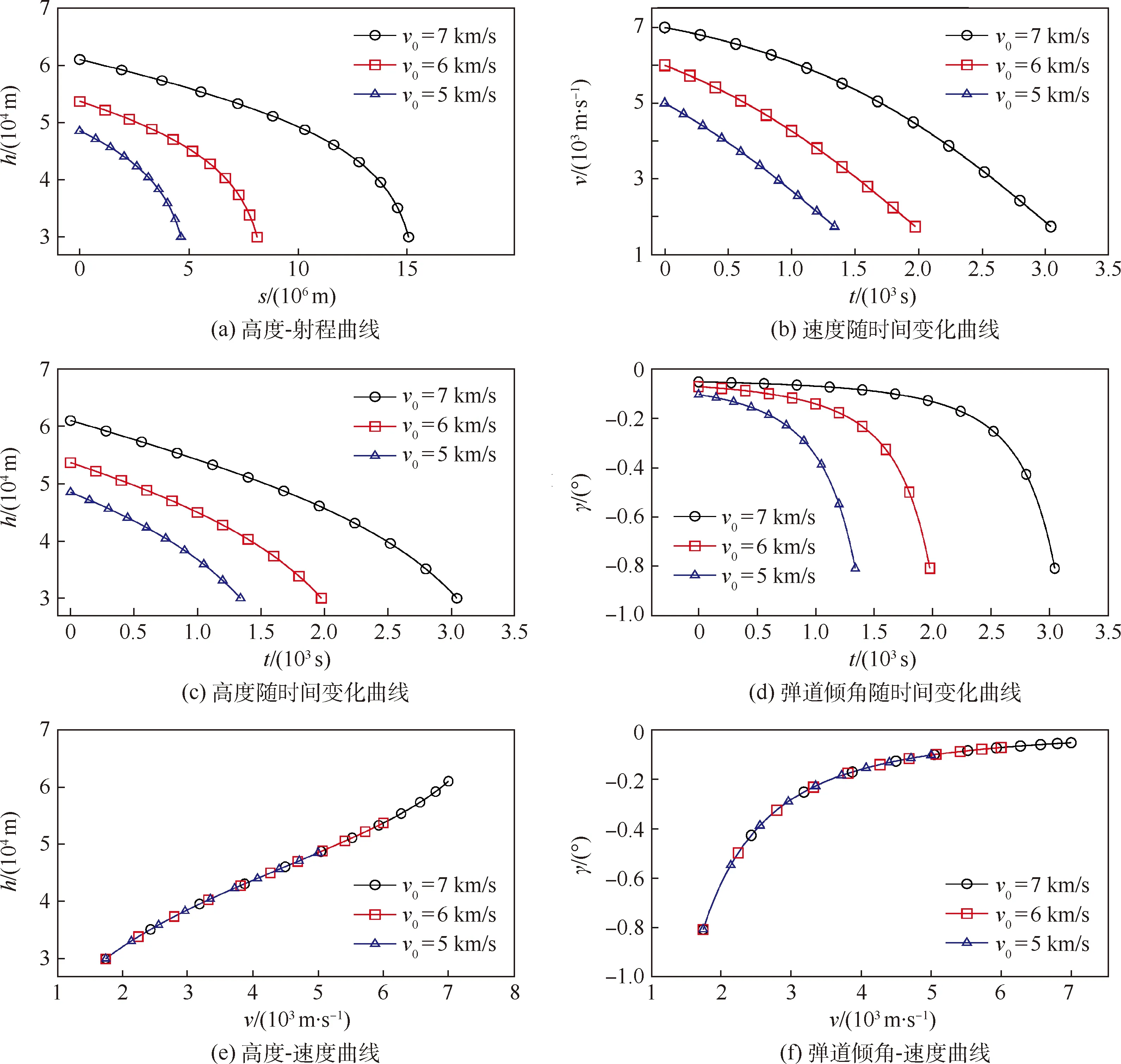
图2 不同初始速度下的平稳滑翔弹道对比Fig.2 Comparison of steady glide trajectories with different initial velocities

4 扰动运动及线性化

从第3节分析可以得出，如果飞行器再入滑翔的起始高度、弹道倾角和速度满足一定关系(在某条平稳滑翔弹道上)，那么飞行器将会一直沿着平稳滑翔弹道飞行。然而实际再入时滑翔初始高度、弹道倾角和速度很可能与期望的平稳滑翔初始状态存在偏差，并且飞行过程中也会存在大气密度、风等多种干扰因素，为了研究这些扰动因素对平稳滑翔弹道的影响，建立如下带有误差干扰模型的动力学方程：

(30)

式中：εL、εD分别为比例形式的升力、阻力干扰输入。同时考虑相对于平稳滑翔弹道存在初始高度扰动δh0、初始弹道倾角扰动δγ0和初始速度扰动δv0的情况。

分析干扰对标准平稳滑翔弹道的影响，最直观的方法就是在实际干扰条件下对方程式(30)求解，再与标准平稳滑翔弹道作差，但是该方法的缺点是计算量大，需要数值求解非线性微分方程，并不是直接分析干扰与弹道偏差的关系，不方便应用于制导[20]。另一种方法是基于小扰动假设的摄动法，将带有误差干扰模型的动力学方程式(30)在标准平稳滑翔弹道附近线性化，得到如下状态空间线性系统：

(31)

式中：

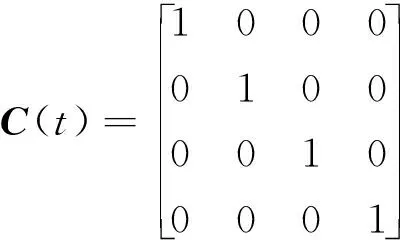
其中：

a12=vscosγs

a13=sinγs

a32=-gcosγs

式中：下标为s的量(包括L、D、g和所有偏导数)指标准平稳滑翔弹道上的数据。所以，系数矩阵中所有分量元素都是时间t的已知函数。线性系统式(31)近似描述了真实弹道偏差的动态特性，即

δh≈h-hs

δγ≈γ-γs

δv≈v-vs

δs≈s-ss

利用第3节获得的初始速度v0=7 000 m/s的平稳滑翔弹道，飞行时间为tf=3 044 s(此时滑翔高度大约为30 km)。以此为标准平稳滑翔弹道，加入常值扰动，然后利用式(30)进行非线性仿真，利用式(31)进行线性系统仿真，得到各状态量的偏差结果如图3所示。本算例中小扰动分别为

(32)

由图3中可直观看出，加入扰动后，滑翔弹道呈现出明显的围绕平稳滑翔弹道振荡的特性；而且线性化系统仿真得到的弹道偏差结果与真实弹道偏差很接近，这说明得到的线性化系统可以很好地近似非线性系统在平稳滑翔弹道附近的动态特性。这为利用线性系统伴随仿真方法分析平稳滑翔弹道奠定了基础。

图3 平稳滑翔弹道小扰动偏差Fig.3 Trajectory deviation from steady glide in case of small disturbance

5 伴随仿真算例分析

利用线性化方程式(31)可以对平稳滑翔弹道进行伴随仿真分析，下面分别对确定性常值小扰动和随机扰动输入进行仿真算例研究。

5.1 确定性常值小扰动

仍然分析第3节中得到的v0=7 000 m/s的平稳滑翔弹道，研究确定性常值小扰动式(32)对终端高度hf=h(tf)的影响，tf=3 044 s，此时滑翔高度大约为30 km。根据式(10)构造系统式(31)的伴随系统，由于考虑高度偏差，取式(31)的输出为y(t)=δh，相应的输出矩阵为C(t)=[1 0 00]；选取伴随系统式(10)的控制v(t)=0，状态初值z(0)=CT(tf)，仿真结果如图4所示。

图4给出了各干扰因素分别导致的终端高度偏差，即(δhf|δh0、(δhf|δγ0、(δhf|δv0、(δhf|εL、(δhf|εD，这得益于伴随仿真的误差预算性质(式(14)～式(16))，(δhf|T表示合扰动结果；图中横轴tgo表示剩余飞行时间，曲线上对应点可以解释为在剩余飞行时间是tgo时，加入相应扰动得到终端tf时刻的高度偏差。为了与实际终端高度偏差对比，利用式(30)对各扰动因素单独(其他扰动设置为0)进行非线性仿真，得到实际终端高度hf与标准平稳滑翔弹道终端高度hsf之差，结果如图5所示。可以看出，非线性仿真与伴随仿真结果很接近，这也再次表明线性化系统式(31)能够很好地反映平稳滑翔弹道在小扰动输入下的动态特性。图5中伴随仿真所有数据是通过一次连续仿真得到，不同扰动因素的影响可以由性质1解释，不同剩余飞行时间tgo的结果可以由性质2得到；而非线性仿真需要针对各不同干扰输入分别进行，在每一个干扰输入下，又需要对tgo循环多次(本算例取循环间隔为10s，大约需要300次)仿真得到，即开始时按照无扰动平稳滑翔弹道仿真，当飞行时间为tf-tgo，或者说剩余飞行时间为tgo时加入相应的小扰动，仿真得到tf时刻的结果。显然，伴随仿真运算量要远小于非线性仿真。考虑到平稳滑翔弹道定义的一致性，tgo可以对应到不同初始速度v0优化得到的平稳滑翔弹道，这样伴随仿真的结果可以解释为不同初始速度的平稳滑翔弹道在加入同样的小扰动式(32)时，导致终端(标准平稳滑翔弹道高度大约为30 km时)高度的偏差；相应的数据可以用于平稳滑翔弹道制导方法的设计与分析。

图4 伴随一次仿真输出各扰动带来的终端高度偏差Fig.4 One adjoint simulation yields terminal height deviation for each disturbance

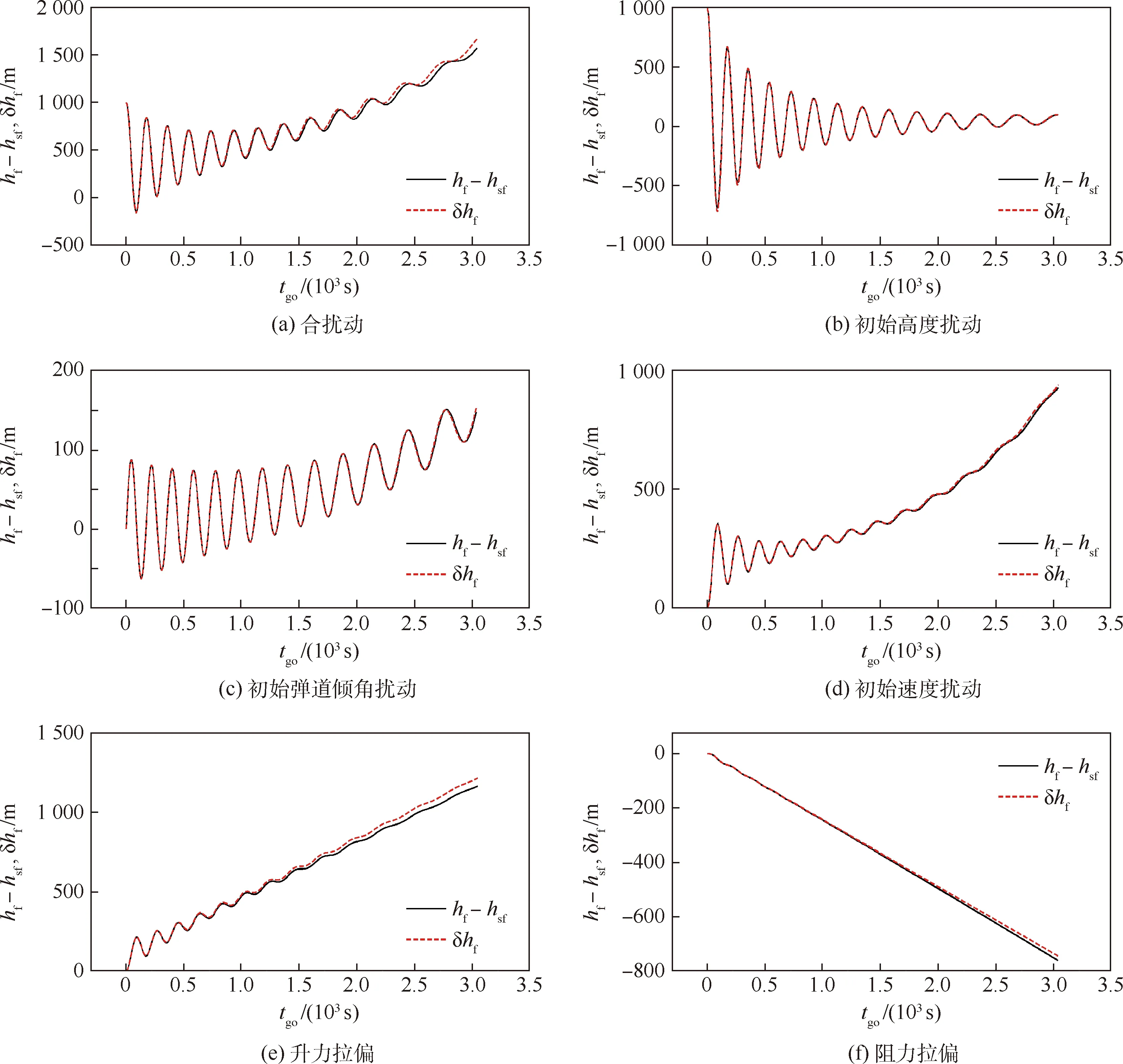
图5 各扰动因素对终端高度偏差的影响(非线性仿真和伴随仿真)Fig.5 Influence of each disturbance on terminal height deviation(nonlinear and adjoint simulation)

从图4和图5还可以得到，在加入常值小扰动式(32)的条件下，初始速度、升力、阻力等小扰动(δv0、εL、εD)对终端高度偏差的影响随tgo增加而增大，而初始高度和初始弹道倾角等扰动(δh0、δγ0)对终端高度偏差的影响随tgo增加振荡衰减；合扰动结果在tgo较小时主要由δh0决定，在tgo较大时，主要取决于δv0、εL、εD等，δγ0影响很小。当需要另计算一组新的小扰动：

导致的终端高度偏差时，不需要重新仿真，利用式(14)～式(16)或线性叠加原理，对已经得到的仿真结果进行简单的线性组合即可。

(kv·δhf|δv0+(kL·δhf|εL+kD·(δhf|εD

类似地，还可以分析确定性常值小扰动式(32)对终端速度、终端射程等影响，只是系统式(31)相应的输出矩阵分别取C(t)=[0 0 10]和C(t)=[0 0 0 1]。仿真结果如图6所示。可以看出，在小扰动式(32)的条件下，影响平稳滑翔终端速度、射程的主要因素为δv0、εL、εD，而且小扰动会带来较大的射程偏差(百公里级)。

为了更清晰地表达各扰动对终端状态的影响，表2～表4分别列出了在不同剩余飞行时间加入单位各扰动导致的终端高度偏差、终端速度偏差和终端射程偏差。其中单位初始高度扰动设为1 km,单位初始弹道倾角扰动设为1°,单位初始速度扰动设为1 m/s,单位升力或阻力扰动设为1%。对比表中数据可以得到，终端状态的偏差关

图6 伴随一次仿真输出各扰动带来的终端速度偏差和终端射程偏差Fig.6 One adjoint simulation yields terminal range deviation and terminal velocity deviation for each disturbance

于初始弹道倾角扰动最敏感，即相比于其他扰动，较小初始弹道倾角扰动会带来较大的终端状态偏差。

5.2 随机扰动

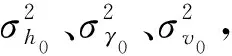
(33)

表2 单位各扰动导致的终端高度偏差Table 2 Terminal height deviation with respect to each disturbance

为便于对比，给出了在合随机扰动条件下终端高度和射程的非线性蒙特卡罗仿真结果，如图8所示。特别地，以终端速度为例，针对每一个单独的随机扰动因素，按照tgo间隔50 s循环(大约60次)，每一个tgo下进行1 000次非线性蒙特卡罗仿真，得到终端速度的散布情况(标准差)，结果如图9所示。

从图8和图9可以看出，伴随仿真结果与多次非线性蒙特卡罗仿真十分吻合，但是蒙特卡罗仿真计算量(非线性仿真次数大约是6×60×1 000=360 000)要远大于伴随一次仿真。

表3 单位各扰动导致的终端速度偏差

表4 单位各扰动导致的终端射程偏差

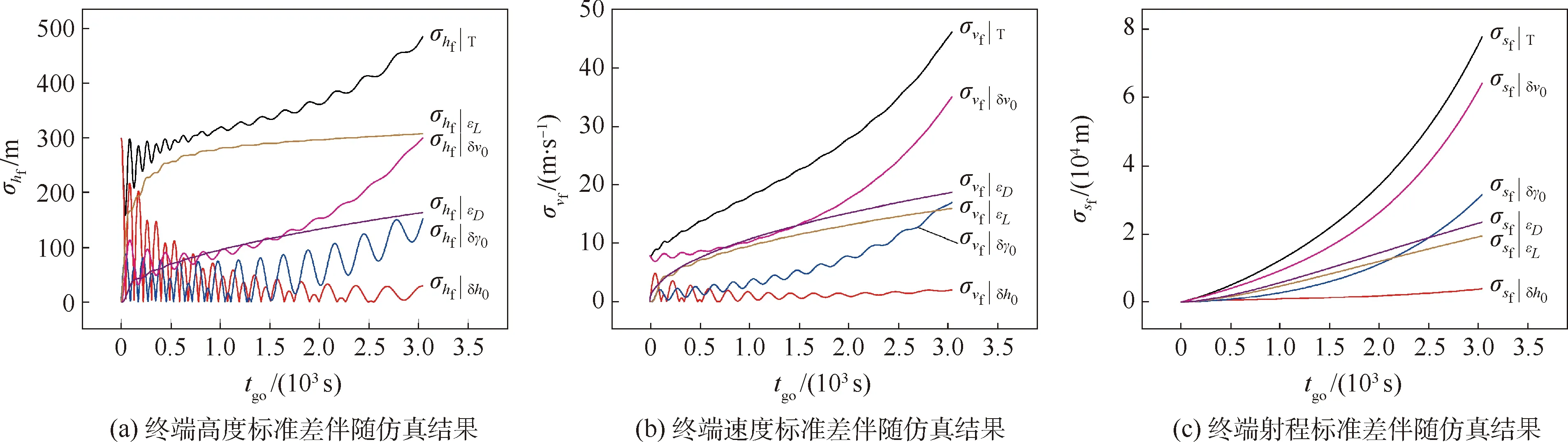
图7 各随机扰动输入下终端高度标准差、终端速度标准差、终端射程标准差伴随仿真结果Fig.7 Adjoint simulation results of standard deviation of terminal height, velocity and range for each random disturbance

图8 合随机扰动下终端高度标准差和终端射程标准差Fig.8 Total standard deviation of terminal height and range with all random disturbances

图9 各随机扰动单独作用时终端速度标准差(非线性蒙特卡罗仿真和伴随仿真对比)Fig.9 Standard deviation of terminal velocity for each random disturbance (comparison between nonlinear Monte Carlo simulations and adjoint simulation)