开关磁阻电机矩角特性模型非线性拟合方法

2019-01-30叶威马齐爽徐萍张珀铭

北京航空航天大学学报 2019年1期

叶威，马齐爽，徐萍，张珀铭

(1. 空间物理重点实验室, 北京 100076； 2. 北京航空航天大学自动化科学与电气工程学院, 北京 100083)

开关磁阻电机(Switched Reluctance Motor, SRM)在磁饱和工作条件下，磁场分布不规则，局部磁路会出现严重饱和，使得其很难精确建模。为分析这些饱和效应以及漏磁现象对电机的影响，目前广泛使用有限元分析方法[1-2]。与实际测量结果的比较表明，有限元方法可以准确地预测开关磁阻电机的矩角特性，具有较高的计算精度，但计算量较大，且对于电机的动态性能分析和控制不够灵活。机电能量转换原理表明，电机输出转矩可以通过磁链-电流-角度(Ψ-i-θ)关系曲线计算得到，因此大多数现有的开关磁阻电机模型都是基于不同转子位置角下的磁化曲线(Ψ-i)得到的[3]。已有的文献提出一系列的开关磁阻电机数学分析[4-7]和仿真模型[8-11]，这些模型结合磁饱和效应来优化开关磁阻电机的控制参数，以降低转矩脉动，但是由这些模型推导出的转矩方程都相当复杂，要求控制器必须具有相当高的运行速度和计算能力，增加了控制器的运算负担和能耗。在文献[12-13]中将非线性磁链特性Ψ(i,θ)或自感特性L(i,θ)，以及矩角特性T(i,θ)数据以表格形式储存起来，简化计算，但查表法需要预先对电机进行测量或者有限元计算，且当实际电流或转子位置角与表格中数值不能完全对应时，必须通过插值求取，查表法具有外推能力差和曲线逼近能力弱的局限性。文献[14-15]则基于电机几何尺寸和定转子材料磁特性等少量信息建立了一种简单非线性磁链模型，该模型实现了实时控制，可应用于控制参数的优化、转矩脉动分析等控制系统的分析和设计中，但是由于模型过于简化，降低了控制精度。

本文通过分析开关磁阻电机的几何形状和铁磁特性，对电机的矩角特性进行了建模分析，并进一步优化了模型中各个参数，该模型将电机瞬时电磁转矩表示为相电流和转子位置角的解析表达式，同样相电流也可表示为转矩和转子位置角的函数。为得到特定的输出转矩，通过此模型可以在线计算相应相电流的参考值，因此在转矩的实时控制中，由这2个表达式很容易快速计算出不同相电流下的矩角特性，且没有了查表法的局限性。同时此模型使得电机磁化曲线和瞬时磁链的计算成为可能，给电机的设计以及电机的驱动控制带来很大的方便。最后为了检验模型精度，以2个样机为例，将新模型的转矩计算结果与有限元仿真和实测结果进行了比较。

1 可逆矩角特性的数学模型的建立

1.1 转矩模型的建立

磁场未饱和时，开关磁阻电机相电感值L只依赖于θ，可记为L0(θ)，此时电机电磁转矩公式为

(1)

记电感L0(θ)对角度θ的导数为L0p(θ)，则磁场不饱和时的电磁转矩T0可以改写为

(2)

为了降低功率变换器的视在容量，通常要求开关磁阻电机工作在高度饱和的状态，其深度饱和的磁通密度B通常能达到1.5～1.65 T[16]，而且其饱和程度是变化的，所以饱和状态下由式(2)得到的转矩将显著偏大。

文献[17]指出在饱和状态下，开关磁阻电机的输出转矩将不再与电流值的二次方成正比，而是随着电流值线性变化。为了确保式(2)在饱和区域的有效性，新的转矩模型参数必须满足以下要求：

1) 在电流很小时，新的转矩公式需与式(2)等效，即转矩与电流平方成正比。

2) 当电流逐渐增大，电机变得饱和时，新转矩方程将从电流的二次函数逐渐变为线性函数。

特别地，当i→∞，即转矩方程从电流的二次函数退化为线性函数，记为

(3)

式中：n为正数;f=f(θ)为转子位置角θ的函数(f>0)，作为曲线拟合时的函数修正。

综上所述，提出以下新的转矩模型，可以保证线性关系与二次关系的合理过渡：

(4)

在式(4)中，电流值i=1/f1/n为转矩和电流的线性关系与二次关系的分界点，参数n影响从二次关系变为线性关系的速率，n越大变化速度越快，n的值与开关磁阻电机的材料、结构以及输出性能有关。显然，电流i的值远小于1/f1/n时，式(4)与式(2)等效，新的转矩模型满足所期望的要求，但对具体参数的确定需要做详细讨论。

注意到转矩方程式(4)是可逆的，当转矩已知时，电流也能由转矩导出：

(5)

式(5)可用于转矩控制时，相电流参考值的计算。

1.2 电感模型的建立

图1为电感L0(θ)及其导数L0p(θ)的理想和实际曲线示意图。理想情况下，电机转子极对着定子槽(θu≤θ<θbo)时，气隙等效电感值保持为最小值，即Lu=Lmin，电感对角度的导数为零，L0p(θu)=0。从定、转子极开始重叠到完全重叠(θbo≤θ≤θeo)这一区间，电感值线性增加，电感对角度的导数为恒定的常数L0pm。从定、转子极完全重叠到两者轴线重合(θeo<θ≤θal)，电感值保持其最大值不变Lal，电感对角度的导数为零，L0p(θal)=0。实际上，考虑到漏磁通和饱和效应的影响，电感及其导数的实际曲线如图中实线所示，特别应该指出的是，在位置θ=θbo和θ=θeo处，气隙的饱和效应最显著。图1中所示的θ1位置，对于大多数开关磁阻电机，都是在转子极旋转到与定子极重合20%的位置角附近。

参数L0pm的值直接决定了L0p以及转矩的峰值，是十分敏感的参数，当对齐位置和非对齐位置的电感值Lal和Lu都已知时，L0pm可以由式(6)计算：

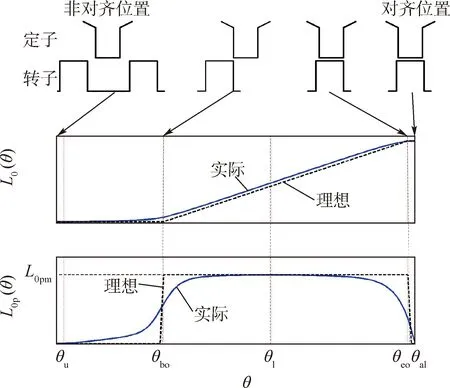
图1 电感L0(θ)及其导数L0p(θ)的理想和实际曲线示意图Fig.1 Schematic of ideal and real curves of inductance L0(θ) and its derivative L0p(θ)

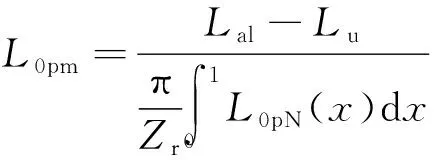
(6)

式中：x=(θ-θu)/(θal-θu)为转子位置角的归一化表示；L0pN(x)为L0p(x)的归一化表示；Zr为转子极数。

在忽略漏磁和铁磁阻的情况下，文献[6]指出，L0pm的大小只与电机的几何尺寸有关，可由式(7)估算：

(7)

式中：μ0为真空磁导率；r1为转子外半径；lst为铁芯轴向长度；δ为气隙宽度；N为相绕组匝数。电机几何外形如图2所示，R1和R2分别为电机定子内、外径；βs和βr分别为定、转子极弧；r2为电机轴径；hr为转子极高。

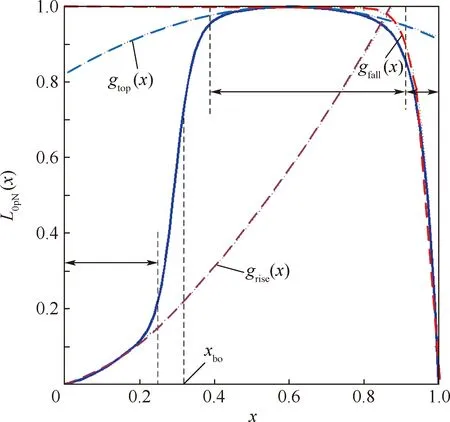
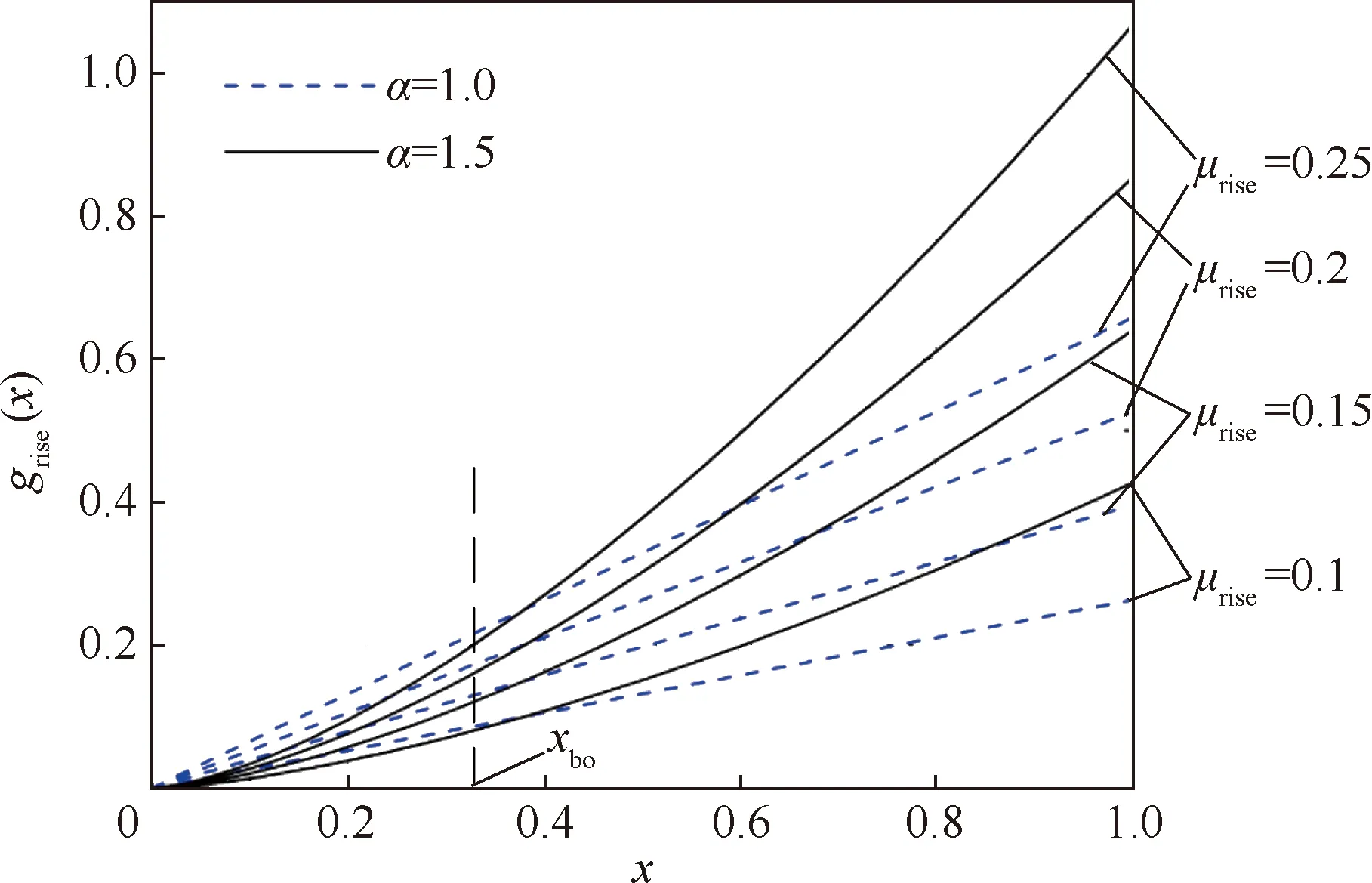
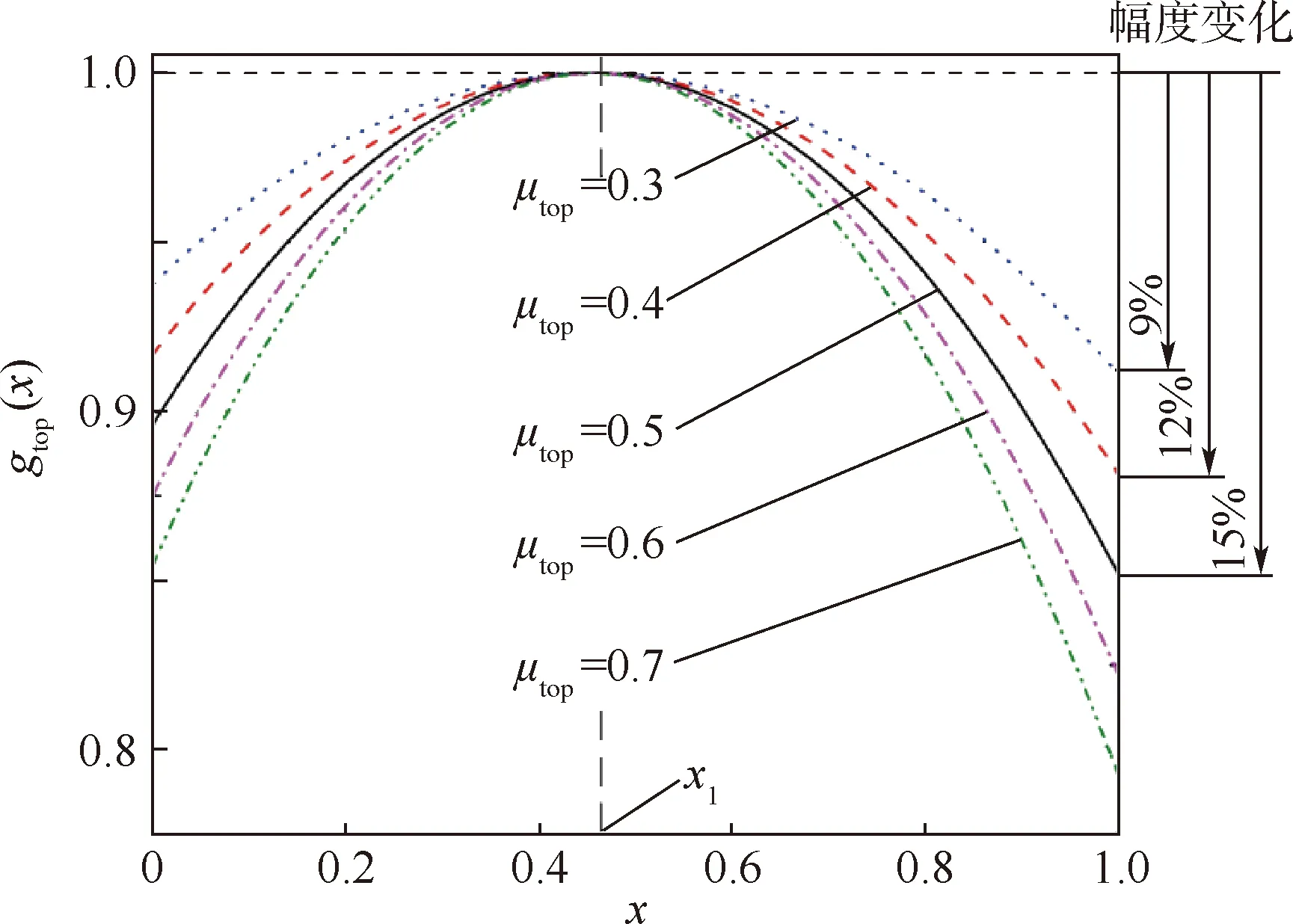
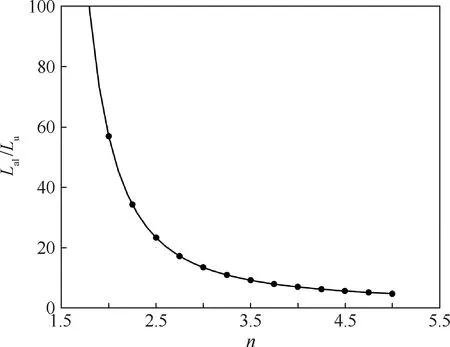
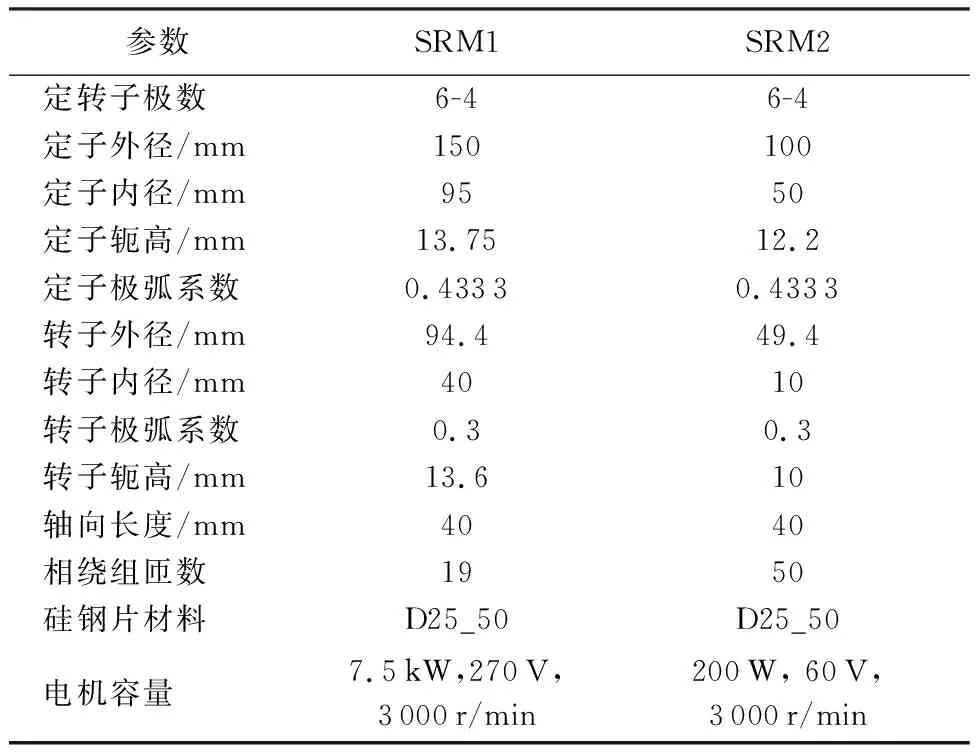
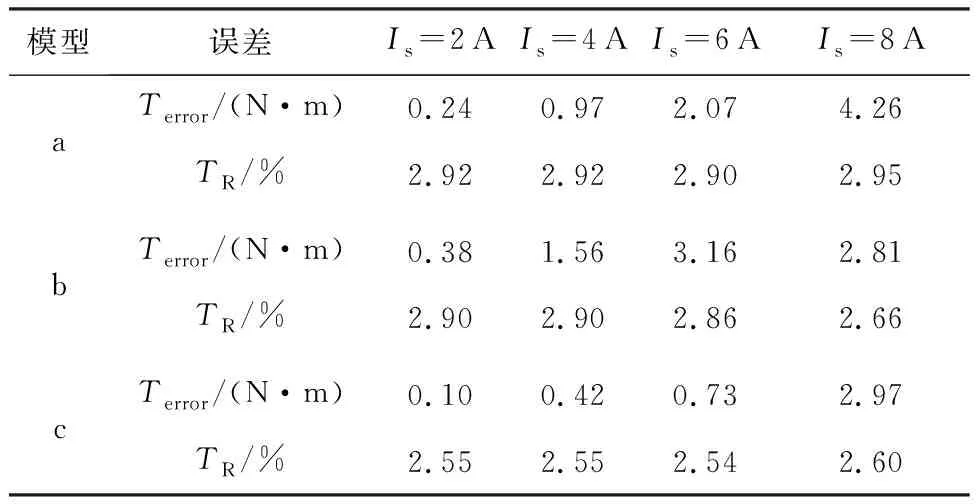
由于L0p(θ)是θ的周期函数，文献[18]采用傅里叶级数方式建立了L0p(θ)等的通用模型，但这种方法需要确定足够高次的傅里叶系数，才能确保良好的精度，如果电机转矩特性未知，各个系数将很难确定。文献[5]对于不同电机转子位置，利用分段函数组的方式表示不饱和相电感L0(或其导数L0p)，但每个分段都只在各自适用区间内有效。图3给出了L0p归一化后的函数L0pN的分段函数表示，xbo是转子极与定子极开始重叠时的归一化转子位置角，xbo=(θbo-θu)/(θal-θu)。grise(x)、gtop(x)和gfall(x)是各个区间的分段函数，grise(x)主要决定了L0pN在区间0≤x

为了突出各个区域分段函数的主要贡献，采用拟合的方式，将3个分段函数放入一个解析表达式中，得到全区域θu≤θ≤θal的函数L0p(θ)解析表达式，拟合方式如下：

图2 开关磁阻电机几何尺寸Fig.2 Physical dimensioning of switched reluctance motor

图3 L0pN由分段函数grise(x)、gtop(x)和gfall(x) 拟合Fig.3 L0pN is fitted by piecewise function grise(x)，gtop(x) and gfall(x)

L0p(x)=L0pm·L0pN(x)

(8)

式中：L0pm为L0p(x)的幅值。L0pN(x)拟合表达式为

(9)

其中：m为充分大的正数。

确定式(9)中的3个函数grise(x)、gtop(x)、gfall(x)及m将是确定L0p(x)的研究重点。这里可以初步确定grise(x)、gtop(x)和gfall(x)的几个特点：

1) 在x=x1位置时(x1是θ1的归一化)，L0p取最大值，则可以确定gtop(x=x1)=1。

2) 相较于区间xbo

3)gfall(x)是为了确保L0p(x)在对齐位置θ=θal附近的快速衰减为0，所以在定、转子极互相偏离较远时，函数gfall(x)的值应等于1，而当定、转子极接近对齐位置即x→1时，函数gfall(x)的值应从1迅速衰减为0。

2 函数L0pN(θ)参数的确定

在转矩模型式(4)中，函数L0p、f及参数n都是未知的，第1节中总结了它们需要满足的要求和一些参数确定的选择方向。在L0pm已经由电机几何尺寸计算得到的前提下，L0p仅决定于L0pN，本节将进一步通过电机几何尺寸确定函数L0pN的各个分段函数和系数的选择。

2.1 m值的选择

在式(9)中，正数m值决定了L0p在x=xbo附近变化的光滑程度，m值越大，过渡区间越窄。当m→∞时，函数grise(x)与gtop(x)在x=xbo将垂直跳跃过渡，过渡区域变为一条竖直线，因此定义条件函数l(x),m应充分大到满足下列条件：

(10)

图4给出了不同的m值所对应的过渡区间，m值应充分大，但并不是越大越好，需要根据xbo的位置合理选择。

图4 不同的m值所对应的过渡区间Fig.4 Transition intervals for different m values

2.2 grise(x)的选择

相对于区间xbo

(11)

式中：常数μrise取决于电机的几何外形；指数α略大于1。由于这一区间的转矩很小，μrise比较典型的取值区间是0.1～0.25，α可以合理地取值为1.5，图5所示为不同α与μrise下的grise(x)曲线。

2.3 gtop(x)的选择

若在x=x1位置时，L0p取最大值，则函数gtop(x=x1)值应等于1，为了描述整个xbo

gtop(x)=1-μtop(x-x1)β

(12)

式中：对于大多数开关磁阻电机，x1一般指转子极旋转到覆盖定子极20%部分的位置角，即x1=xbo+0.2(1-xbo)。图6所示为不同μtop下的gtop(x)曲线，β取值为2。

常数μtop决定了L0p在x≠x1位置的下降速度，对于样机1(xbo=0.31，x1=0.45)仿真结果表明，当电机电流为常值时，因相电感的影响导致电机的转矩有约15%的幅度变化，从图6中可以看出，μtop比较好的取值是μtop=0.5。

图5 不同α与μrise下的grise(x)曲线Fig.5 Curves of grise(x) for different α and μrise

图6 不同μtop下的gtop(x)曲线Fig.6 Curves of gtop(x) for different μtop

2.4 gfall(x)的选择

在定、转子极未对齐时，函数gfall的值等于1，而当定转子极接近对齐位置即x→1时，函数gfall的值应迅速衰减为0，所以一种可能的表达式为

(13)

式中:系数μfall通常取1即可。

由于大多数电机定、转子极宽度接近(一般转子极要宽一些)，只要正整数k值取的充分大，式(13)能够满足这些电机的特性。然而，对于那些定、转子极宽度显著不同的电机，在x=xeo和x→1处gfall衰减幅度将显著不同，为了将这种性质加入，式(14)将更合理：

(14)

式中：xeo为定、转子极钢开始完全重叠时的归一化位置角。当k→∞时，由式(13)和式(14)将得到gfall(0

图7 不同k下的和的曲线Fig.7 Curves of and for different k

3 模型参数n与函数f(θ)的确定

本节将研究参数n所受到的约束条件，并确定修正函数f(θ)。

3.1 参数n的确定

显然对于任何开关磁阻电机，无论转角θ和电流i取何值，磁链都应该是电流的单调递增函数，即

(15)

磁链与转矩满足：

(16)

由式(4)、式(15)和式(16)可得

(17)

为了简化分析，在这里假定式(17)被积函数中的f是不变的常数，则可得

(18)

显然，当n≤1时，不等式(18)恒成立，当n>1时，不等式左边对电流求导，使得不等式左边取极值的电流值为

(19)

将式(19)代入式(18)，并取L(θ)在对齐位置的最大值L(θ=θal)=Lal，将得到一个满足式(17)的必要条件：

(20)

在式(20)中，相绕组等效自感最大值与最小值之比Lal/Lu受到参数n值的约束，两者关系曲线如图8所示。

图8中，当n=3时，Lal/Lu=13.4，对大多数实际电机，受到材料和结构的限制，Lal/Lu比值都不会超过这个值，特别是考虑到严格计算还要超出20%以上，因此对大多数的开关磁阻电机，参数n值选择n=3将是最佳。

图8 Lal/Lu值与n的关系曲线Fig.8 Curve of relationship between value of Lal/Lu and n

3.2 函数f(θ)的确定

综合考虑电机的特点，f(θ)需要满足2条特性：

1) 在定转子极不重叠区间(即θu≤θ≤θbo)，电机磁场未饱和，特别是在非对齐位置角θ=θu附近，电磁转矩的非线性方程式(4)将退化为线性方程式(3)，从而可知当θ→θu时，f(θ)→0。

2) 在位置x=xbo和x=xeo处气隙的饱和效应最为显著[19]，这意味着f(x)在这2个位置取极大值。

根据这2条特性，在区间xbo≤x≤xeo，f(x)可以表示为

(21)

式中：预设了3个常数c、c1、c2，为了确定这3个数，首先必须假设c足够大，使得f(x=xbo)≈c1且f(x=xeo)≈c2。

1) 常数c2

在x=xeo时，气隙磁链和电流偏离线性关系，磁路临界饱和，∂T/∂i将达到最大值，即

(22)

由式(4)和式(22)可得

(23)

(24)

在式(21)中有f(x=xeo)≈c2，所以联立式(21)、式(23)和式(24)可得

(25)

式中：典型的临界饱和磁通密度Bs范围是1.2～1.5T。

2) 常数c1

在电机深度饱和时，即x=x1，i→∞时，电磁转矩可由式(3)计算，但深度饱和时的电磁转矩满足：

Tem=Bsatr1lstNi

(26)

式中：Bsat为电机深度饱和时的磁通密度，典型范围是1.5～1.65T。电机深度饱和时，电流记为Isat，同理，Isat与Bsat也满足式(24)。由式(3)和式(26)可得

(27)

实际上，对于大多数开关磁阻电机，x1=xbo+0.2(1-xbo)，为简化分析，可以认为

f(x)|x=xbo=λnf(x)|x=x1

(28)

式中：λ为常数，表示等式两边为简单的比例关系，经过大量的实验和仿真验证，其典型的取值范围为1≤λ≤1.3。

在式(21)中有f(x=xbo)≈c1，所以由式(21)、式(27)和式(28)可得

(29)

3) 常数c

对于一般的开关磁阻电机，x1≈(xbo+xeo)/2，所以将x1代入式(21)可得

(30)

将式(25)、式(27)和式(29)代入式(30)可得

(31)

从本节可知Bsat和Bs的值很接近，除非特别必要的地方，可在式(31)及后面的分析中，取Bsat=Bs，简化分析过程。于是，由式(24)、式(25)、式(27)和式(29)可有以下推论：

(32)

(33)

(34)

为了在区域0≤x

(35)

由推论式(32)～式(34)可知，将f(x)归一化处理只需要将f(x)与Isn相乘即可。故在式(21)和式(35)中，将各参数取值为n=3，λ=1.2，m=13，则归一化的f(x)与f1(x)的曲线如图9所示，显然，图中的f1(x)满足f的2条特性。

图9 归一化的f(x)与f1(x)的曲线(n=3,λ=1.2,m=13)Fig.9 Normalized curves of f(x) and f1(x)(n=3,λ=1.2,m=13)

4 可逆矩角特性模型的有限元计算与实验验证

将表1中所列的2个开关磁阻样机在有限元软件中各自建立计算模型，得到电机转矩的有限元计算结果，如图10所示，图10(a)为样机SRM1和SRM2的有限元三维模型，图10(b)为SRM1不同转子位置的瞬态场的计算结果。

为验证解析模型的准确性，将样机SRM1的有限元模型与模型解析结果进行比较。图11给出了有限元模型结果，其中各曲线所对应的相电流值从0A开始每次增加1A，最大相电流值为8 A。由于解析表达式(4)中的参数在各自允许的范围内是可以合理调整的，图12(a)、(b)和(c)分别为在不同的解析模型参数下的结果对比，各解析模型(a、b和c)的参数取值列于表2中。

表1 两个开关磁阻样机的主要参数Table 1 Main parameters of two SRM prototypes

图10 两个样机的有限元模型及SRM1的磁路仿真结果Fig.10 Finite element models of two prototypes and magnetic simulation result of SRM1

在图12中，电机输出正转矩和负转矩区间的曲线形状是成中心对称的，由3个解析模型的对比结果可知，对于确定尺寸的开关磁阻电机，表征其转子位置角的模型参数xbo、x1和xeo只与电机的几何形状相关，所以在解析模型中是固定值。而电机的材料决定了相绕组电感导数L0p(x)的曲线形状，进而决定了转矩曲线的形状，所以在图中的3个解析模型中，参数μrise、μtop、μfall和α、β的值也都相同。最后，m值影响了0

图12 样机SRM1有限元模型与不同模型参数的解析模型结果对比Fig.12 Result comparison between finite element model and analytical model with different model parameters for prototype SRM1

作为结果比对，表3计算了不同相电流下，图12(a)、(b)和(c)中解析模型结果与有限元计算结果的绝对误差Terror及平均相对误差TR,其计算式如下：

(36)

(37)

式中：TFEM为有限元计算的输出转矩；TModel为解析模型计算的输出转矩；j为采样点编号；Ns为总采样点。

从表3可以看到，从平均相对误差指标上看，模型c好于模型b好于模型a。从绝对误差指标上看，模型a在相电流较小时比较准确，模型b在相电流较大时比较准确，而模型c，除在相电流值8 A时绝对误差稍偏大外，无论是绝对误差还是平均相对误差指标上均优于前两者。所以对于样机1，模型c是最优选择。

解析模型结果，有限元的计算结果和实验测量结果的对比如图13所示，从图中可以看出矩角特性曲线的解析计算结果与有限元结果基本一致，与实验测量结果误差不超过3%，误差最大值在转子对齐位置处。与实验测量结果误差原因一部分是在电机的对齐位置，输出转矩值随位置角的变化非常剧烈，这一点从曲线图下降趋势可以看出，所以在此位置转子的微小扰动对测量结果的影响是很明显的。

对于样机SRM2，解析模型各参数的取值列于表4中，其有限元计算结果和解析模型结果的对比如图14所示，从图中可以看出矩角特性曲线的解析计算结果与有限元计算结果完全一致。