数学文化彰显数学魅力
2019-01-29广东省广州市增城区荔城中学黄结伟
广东省广州市增城区荔城中学 黄结伟
数学是一切知识的最高形式,是一切科学的基础,可以说人类的每一次重大进步背后都是数学在后面强有力的支撑。数学是一种工具、也是一种思维模式,更是一种素养。数学核心素养是指能从数学角度看问题,有条例地进行理性思维、严密求证、逻辑推理和清晰准确地表达的意识和能力。对于中学生来说,学好数学不仅关系到升学问题,更是为未来发展打下扎实的基础。如何培养学生的数学核心素养是学好数学的关键。培养学生数学核心素养是当前教育领域的共识。
数学文化在培养学生数学核心素养的过程中有着重要的作用。如何将数学文化渗透到日常教学中,让学生感受到数学文化的熏陶,利用数学文化育人的同时,发展学生的核心素养。
在《高中数学课程标准》中,将体现“数学文化价值”作为高中课程标准的理念之一,强调“数学文化”是贯穿整个高中数学课程的重要内容,与此同时,教育部公布的《关于2017年普通高考考试大纲修订内容的通知》对能力立意的考查有所加强,同时特别指出增加了数学文化知识的考查。数学文化的植入,让学生了解数学在人类文明发展中的作用,增强数学文化意识,彰显了数学的文化价值。
其实数学文化与传统命题的素材一点都不冲突,它能巧妙地在每个知识模块或专题中,很多编题人迅速地在数学试题中融入了数学文化,加深了学生对数学历史文化的了解,同时加强学生的数学文化修养。与此同时,也不断加强和培养了学生的数学应用意识,让数学贴近生活,无处不在。
下面是笔者整理了多套试卷中的多个试题来分析如何在考试中更好地融入数学文化,提高学生的数学应用意识,以助学生提高兴趣的同时也能加强对数学文化的认识。
一、以数学名人取材,渗透数学文化
例1.(2018年全国II卷理科数学试题第8题)我国数学家陈景润在哥德巴赫猜想的研究中取得世界领先成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )

例2.(2018年广州一模理科试题)我国南宋数学家杨辉所著的《详解九章算术》中,用图①的 三角形形象地表示了二项式系数规律,俗称“杨辉三角形”.现将杨辉三角形中的奇数换成1,偶数换成0,得到图②所示的由数字0和1组成的三角形数表,由上往下数,记第n行各数字的和为Sn,如S1=1,S2=2,S3=2,S4=4,……,则S126=______.

数学家的历史某种意义上反映的就是数学史,试题在考查数学知识的同时,也渗透数学文化的考查,引领学生重温历史,展示数学家们研究数学问题的风采。例1中借助我国数学家陈景润在哥德巴赫猜想的研究中取得世界领先成果为背景命制了一道古典概率计算问题,使考生潜移默化地感受我国数学取得的成就。例2借助杨辉三角形为背景命制了一道数列的计算问题,使考生感受到知识的理解与应用,感受到杨辉三角形的魅力,感悟数学的发现并不神秘,数学家而是从常规问题入手的。
二、以数学名著取材,弘扬优秀文化
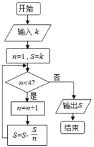
例3:(1)我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
A. 4. B. 6 C. 7.5 D. 9
(2)《九章算术》中有如下问题:“今有勾五步,股一十二步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边分别为5步和12步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是( )

(3)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知1丈为10尺,该锲体的三视图如图所示,则该锲体的体积为( )
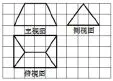
A. 10000立方尺 B. 11000立方尺 C. 12000立方尺 D. 13000立方尺
《九章算术》是中国古代的数学专著,是"算经十书"(汉唐之间出现的十部古算书)中最重要的一种。《九章算术》的内容十分丰富,全书采用问题集的形式,收有246个与生产、生活实践有联系的应用问题,其中每道题有问(题目)、答(答案)、术(解题的步骤,但没有证明),有的是一题一术,有的是多题一术或一题多术。这样的题目让学生不仅能将生活问题转化为数学问题去解决,还能感受到《九章算术》的博大精深,同时培养学生的逻辑推理的核心素养,培养学生敢于去探索思考问题的精神。
所以今后我们的教学中,如果能更好的以数学名人,数学名著、古文或数学历史,作为学习背景和试题背景,相信能吸引更多的学生能积极参与数学的学习与研究,不断地提升学生的数学核心素养,加强应用意识。
弘扬数学文化,弘扬优秀传统文化,更彰显数学的魅力!
