挖掘考题中的数学史，让数学不枯燥

武汉市钢都中学 梅柳红

随着新课程的实施，教材中数学史的内容所占比例大幅增加，但从教学实际来看，数学史受重视的程度并未发生太大的改变，挖掘高考中的数学史因素，并有效应用于教学，是将数学史和高中数学教学结合的有效途径。下面我们一起来欣赏近年来高考卷中的数学史，借以说明数学史的人才选拔功能。

例1.（2006年湖北卷第15题）将杨辉三角中的每一个数都换成分数，就得到一个如图所示的分数三角形，称为莱布尼茨三角形。从莱布尼茨三角形可看出：，其中x=___

例2.（2007年高考湖南卷理科15题）将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表.从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n次全行的数都为1的是第___行；第61行中1的个数是 .

答案：2n-1，32

数学史背景链接：杨辉三角。

“杨辉三角”，也称“贾宪三角”，在西方文献中则成为“帕斯卡三角”。贾宪是北宋人，约公元1050年完成一部叫《黄帝九章算术细草》的著作，原书丢失，但其主要内容被南宋数学家杨辉著《详解九章算法》（1261）摘录，因能传世。“杨辉三角”，它实际上是一张二项系数表，与我们现在的学习联系最紧密的是二项式展开式的系数规律。杨辉三角最本质的特征是：它的两条斜线数字都是1，而其余的数则是等于它肩上的两个数之和。宋元时期是中国古代数学发展的高峰时期，也是中国数学史上名家辈出、成果迭起的重要时期，“杨辉三角”的发现就是其中精彩的一页，在竞赛中也常常会用到，最简单的就是叫你找规律。

例3.（2007年湖北卷第21题）已知m,n为正整数.

(Ⅰ)用数学归纳法证明：当x＞-1时，(1+x)m≥1+mx；

解答：（Ⅰ）证：用数学归纳法证明：

（ⅰ）当 m =1时，原不等式成立；

∵ x2≥0，∴左边≥右边，原不等式成立；

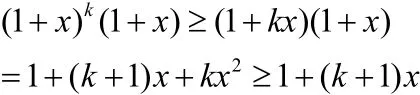
综合（ⅰ），（ⅱ）知，对一切正整数m，不等式都成立。

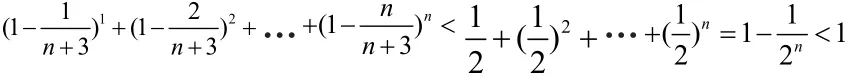
即当 n ≥ 6 时，不存在满足该等式的正整数n

故只需讨论n=1，2，3，4，5的情形，

当n=1时，3≠4，等式不成立；

当n=2时，32+42=52，等式成立；

当n=3时，33+43+53=63，等式成立；

当n=4时，34+44+54+64为偶数，而74为奇数，

故34+44+54+64≠74，等式不成立；

当n=5时，同n=4的情形可分析出，等式不成立；

综上，所求的n只有n=2，3.

数学史背景链接：伯努利不等式，埃斯柯特（Escott）猜想。

第(Ⅰ)问所要证明的不等式实际上是伯努利（Bernoulli）不等式的一个变式，伯努利不等式的一般形式为：

设x＞-1，则当0＜α ＜1时，有(1+ x )α≤1+ α x ，而当α ＜0或α ＞1时，有(1+ x )α≥1+ α x，当且仅当 x = 0 时取等号。

第（Ⅲ）问是数论中典型的不定方程问题，它源于埃斯柯特（Escott）猜想，而埃斯柯特是基于波文（Bowen）猜想：方程没 有非平凡解 (平凡解指,即1+2=3)。而Escott猜想是柯召等人进行研究的，它比Bowen猜想更具有一般性：当n＞1时，关于n，h，x的方程的正整数解只有（n，h，x）=（2，1，3），（3，2，3）。.对于第（Ⅲ）问，只是Escott猜想的一个特殊情况，即令，仅求n。

与此如出一辙的还有商高定理（即勾股定理）的推广：

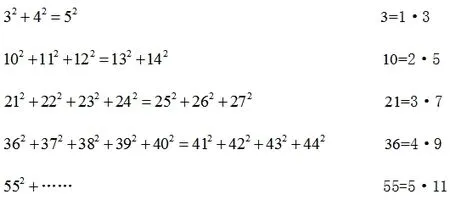
一般而言，证明：

商高定理在中国有悠久的历史，可以上溯到大禹治水时代（公元前21世纪）或周公时代（公元前11世纪）。普遍定理至晚到陈子时代（公元前6、7世纪）已经明确认识并广泛应用。而后人对前人的成果予以加工，得到的结构也是妙不可言。

例4.（2008年湖北卷第15题）观察下列等式：

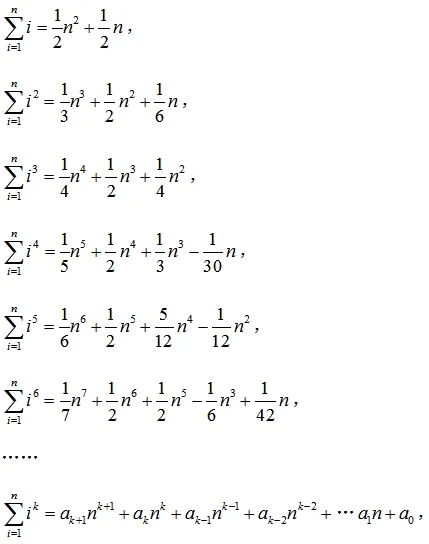
数学史背景链接：垛积术。

南宋的杨辉在《详解九章算法》中明确提出了一些高阶等差数列的求和公式，朱世杰在这方面获得系统和普遍结果。朱世杰在《四元玉鉴》中给出了一系列所谓“三角垛”公式：

……

这样，朱世杰相继以前一个级数的和作为新级数的一般项，就得到了P阶等差级数求和的一般公式：

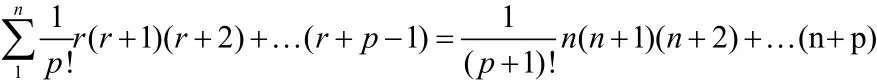
从北宋到元代中叶，中国数学有了一套严整的系统和完备的算法，是中国古代数学的全盛时期，这时欧洲还处在中世纪，中国数学家光辉灿烂的成就远远走在世界的前列！

例5.（2009年湖北卷第10题）古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如：

他们研究过图1中的1，3，6，10，……，由于这些数能够表示成三角形，将其称为三角形数；类似地，称图2中的1，4，9，16，……这样的数为正方形数。下列数中既是三角形数又是正方形数的是（ ）

A.289 B.1024 C.1225 D.1378

把四个选项的数字，分别代入上述两个通项公式，可知使得n都为正整数的只有1225.

例6.（2006年高考数学广东卷第14题）在德国不莱梅举行的第48届世乒赛期间，某商场橱窗里用同样的乒乓球成若干堆“正三棱锥”形的展品，其中第一堆只有一层，就一个球，第2、3、4 堆最底层（第一层）分别按图所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第n堆 n层就放一个乒乓球，以f(n)表示第n堆的乒乓球总数，则 f (3) =_____， f (n) =______.

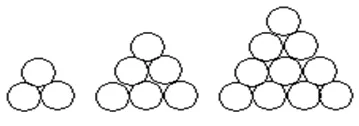
数学史背景链接：形数。

毕达哥拉斯很注意形与数的关系。“形数”（figurate number）就是形与数的结合物，如本题中的三角形数、正方形数。诸如此类的还有五边形数、六边形数等。这一类数列现在可归入高阶等差数列的范围。用同样的方式可以定义所有的多边形数。这一过程还可以推广到三维空间去构造多面体数。“形数”体现了数与形的结合。除此之外，毕达哥拉斯学派还给出了其他数形结合的例子，如毕达哥拉斯三元数组：（m为奇整数），它们分别表示一个直角三角形的两条直角边和斜边，与勾股定理密切相关。关于数的研究，还有很多例子，反映了古代人的智慧，值得我们好好学习。

解答：由a6=1，得a5=2，a4=4，a3=1或8，a2=2或16，a1=4或5或32

数学史背景链接：角谷猜想

角谷猜想，在西方它常被称为西拉古斯（Syracuse)猜想，因为据说这个问题首先是在美国的西拉古斯大学被研究的；而在东方，这个问题由将它带到日本的日本数学家角谷静夫的名字命名，被称作角谷猜想。它的问题是：从1到n的任何一个自然数, 只要对n反复进行下列两种运算：如果n是偶数, 就除以2 ；如果n是奇数, 就乘以3加1，最后的结果总是1。今天在数学文献里，大家就简单地把它称作“3x +1问题”。因为这是个形式上很简单的问题，要理解这个问题所需要的知识不超过小学三年级的水平，所以每一个数学爱好者都可以来碰碰运气，试试是不是能证明它。不乏天才和世界上第一流的数学家，他们都没有成功。数论学家保尔•厄尔多斯(Paul Erdos) ：“数学还没有准备好来回答这样的问题。”

例8.（2009年高考数学湖北卷文科第9题）设,xR∈记不超过x的最大整数为[x],令{x}=-[x]，则

A.是等差数列但不是等比数列

B.是等比数列但不是等差数列

C.既是等差数列又是等比数列

D.既不是等差数列也不是等比数列

数学史背景链接：黄金分割

例9.（2007年高考数学北京卷第13题）2002年在北京召开的国际数学家大会，会标是我国以古代数学家赵爽的弦图为基础设计的。弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形（如图）。如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么cosθ的值等于______.

解答：由题意可知，大、小正方形边长分别为5、 1.设直角三角形较短边长为a，则

另外一方面，由勾三股四弦五，直接检验也可以快速解决问题。

数学史背景链接：勾股定理

勾股定理又叫商高定理，或称毕达哥拉斯定理。在一个直角三角形中，斜边边长的平方等于两条直角边边长平方之和。据考证，人类对这条定理的认识，少说也超过4000年！中国最早的一部数学著作——《周髀算经》，就有这条定理的相关内容。我们可以清楚地看到，我国古代的人民早在几千年以前就已经发现并应用勾股定理这一重要的数学原理了。 在西方有文字记载的最早的证明是毕达哥拉斯给出的。据说当他证明了勾股定理以后，欣喜若狂，杀牛百头，以示庆贺，故西方亦称勾股定理为“百牛定理”。遗憾的是，毕达哥拉斯的证明方法早已失传，我们无从知道他的证法。

勾股定理是几何学中的明珠，它充满魅力，千百年来，人们对它的证明趋之若鹜，其中有数学家、画家，也有业余数学爱好者，比如一位美国国家总统也给出过一种很经典的方法。1940年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑，其中收集了367种不同的证明方法。实际上还不止于此，关于勾股定理的证明方法已有500余种，仅我国清末数学家华蘅芳就提供了二十多种精彩的证法，这是其它任何定理无法比拟的。

在一般人看来，数学是一门枯燥无味的学科，因而很多人视其为畏途。从某种程度上说，如果在数学教学中渗透数学史内容而让数学活起来，这样便可以激发学生的学习兴趣，也有助于学生对数学概念、方法和原理的理解与认识的深化。而以高考题为线索去了解数学史，使得枯燥的文字介绍多了一层理论基础，同时也使得单调的数学试题，笼罩了一层历史的神秘美感。