权重适配的布拉格峰展宽方法
2019-01-28汪金龙AlbertoCruz刘铮铮雷海韦瑶张炜彭晟
汪金龙,L.Alberto Cruz,刘铮铮,雷海,韦瑶,张炜,彭晟
1.新瑞阳光粒子医疗装备(无锡)有限公司,江苏无锡214021;2.南京大学物理学院,江苏南京210093;3.国家超级计算无锡中心,江苏无锡214021
前言
放疗在癌症治疗中起着越来越重要的角色[1]。近几年我国内地更是掀起了质子重离子放疗的热潮,继山东万杰质子医院和上海质子重离子医院开业后,多个质子重离子中心陆续开始建造[2]。蒙特卡洛方法能够全面模拟粒子与物质的相互作用[3],近些年,蒙特卡洛程序逐步应用到质子重离子医疗中[4],不同程序相互验证也尤其重要[5]。蒙特卡洛程序在质子重离子放疗领域中,尤其在辐射防护[6]、探测器设计[7]、治疗计划[8]等方面的应用越来越广泛[9]。
布拉格峰展宽(Spread-out Bragg Peak,SOBP)方法[10]一直是质子重离子放疗领域的研究重点[11],对临床应用有着重要的意义[12-13]。本文根据盖格法则[14]和Bortfeld等[10]工作成果,提出一种权重适配的SOBP方法,并通过蒙特卡洛模拟,验证该方法的有效性。
1 资料与方法
本文以质子(70~230 MeV)在水中的SOBP为研究对象,其他粒子和介质及其组合可结合本文研究方法类推。
1.1 质子能量-射程
质子能量大于10 MeV,其射程和能量关系很好地满足盖格法则:

其中,E是入射质子初始能量,R是质子在介质中的最大射程,α和P是拟合系数。当能量单位取MeV,射程单位取cm,ICRU 49号报告给出在水中α≈2.2×10-3、P≈1.77[15]。为了得到新的数据,我们用FLUKA[16-17]重新计算质子在水中的射程,步长取10 MeV,拟合得到α=2.56×10-3、P=1.738,如图1所示。

图1 质子在水中的能量-射程Fig.1 Proton rang-energy relation in water
对比FLUKA和MCNPX两种蒙特卡洛程序计算的射程发现,FLUKA的计算结果都偏小约1%~2%[18],这种偏差可能是计算模型的差异造成的,如表1所示,在我们的模型中质子先穿过一定厚度的空气再进入水体,在空气中质子也会损失很小的一部分能量。
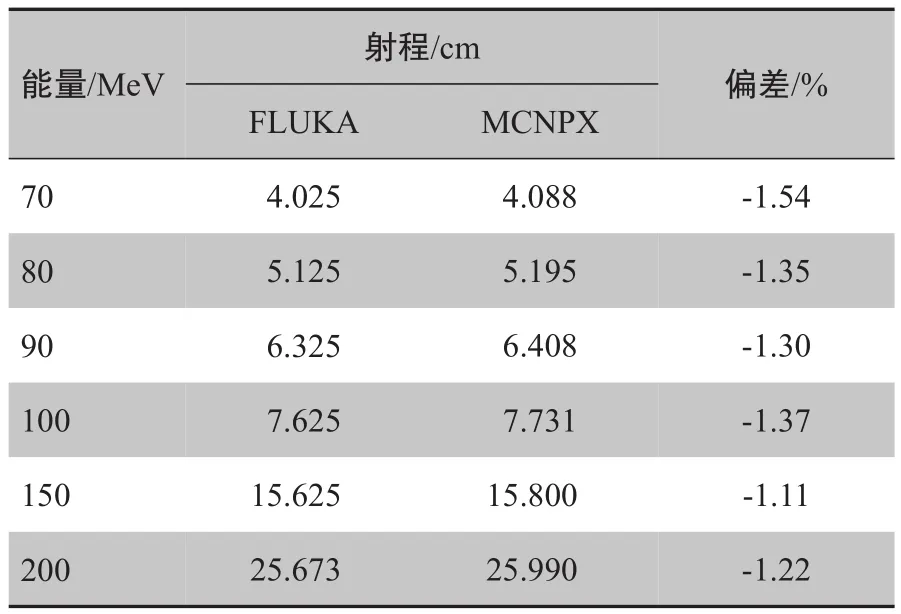
表1 质子射程FLUKA和MCNPX模拟对比Tab.1 Simulated proton range in FLUKA vs MCNPX
为提高计算速度,将FLUKA部署在国家超级计算无锡中心计算机集群上,实现并行运算,使单机几小时的计算量可在几分钟内完成。
1.2 能量权重函数
SOBP方法的核心是配置不同能量质子的权重,Bortfeld利用拉普拉斯变换,从数学上解析求解了权重函数,参见文献[10]附录A。

其中,ρ是介质密度,D0是目标剂量,SOBP的宽度范围为[dmin,dmax],离散化形式公式为:

1.3 蒙特卡洛模型
本文采用蒙特卡洛程序FLUKA模拟计算SOBP。为更接近临床情景,本文采用x=3 cm、y=4 cm面均匀分布的平行束质子入射到10 cm×10 cm×50 cm的长方体水模中,入射点距离水模表面z=-0.001 cm,如图2所示。
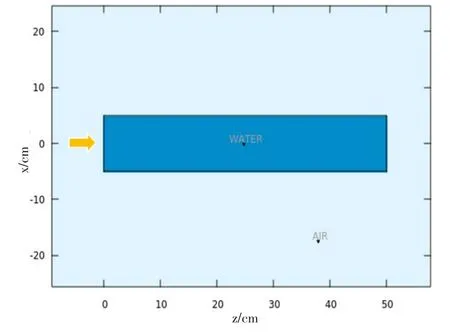
图2 FLUKA计算几何模型Fig.2 FLUKA geometry model
剂量计算选取FLUKA默认的吸收剂量,考虑质子入射后所有种类射线的总和剂量。对每一套参数均输入5 000 000个“质子”,可得到较好的统计,误差小于±0.5%,如图3所示。
1.4 展宽布拉格峰
我们发现,直接用拟合的P=1.738代入式(2)并不能得到平坦的SOBP,如图3所示。可见由式(2)计算的权重在低能区偏高,在高能区偏低。由于M已归一化到权重值,图中给出的是相对剂量分布,后同。
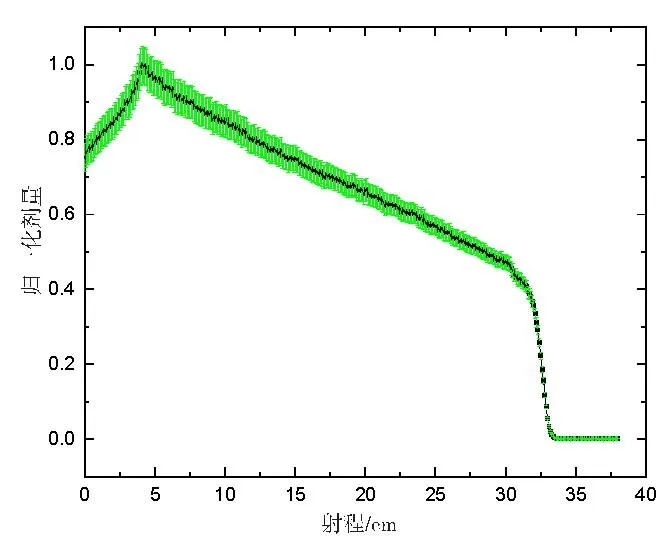
图3 方程(2)得到的SOBPFig.3 Derived spread-out Bragg peak(SOBP)from equation(2)
通过调节参数P,Bortfeld等[10]得到的解析解才能够得到理想的SOBP。Jette等[12]改进了权重函数,但仍需调节参数P才能得到较为平坦的SOBP,并且对于较宽的SOBP,中间区有向下坍塌的趋势。
2 权重函数适配法展宽布拉格峰
2.1 展宽布拉格峰
为解决上述问题,本文提出权重函数适配法展宽布拉格峰。观察图3发现SOBP中间区剂量与射程成线性关系D=a+bR,拟合[dmin,dmax]区域,得到a=1.842 02、b=-0.033 71。为了降低低能区权重,增加高能区权重,自然地定义适配函数F(R):

其中,k为敏感参数,用适配函数F(R) 乘以式(2)得到新的权重函数:

随着k的增加,低能区权重降低,高能区权重增加,当k=0时回到式(2),如图4所示。
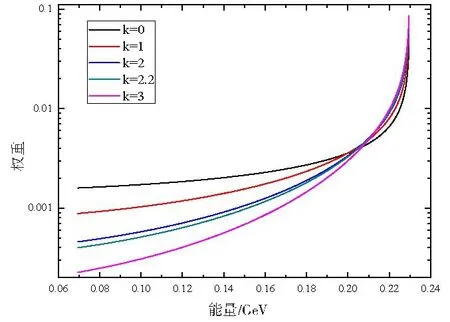
图4 适配法权重Fig.4 Weight adaption with different k
根据式(5)得到权重函数适配法展宽的布拉格峰,如图5所示,当k=2.2时得到最平坦的SOBP,中间平坦区偏差不超过±2%,并且消除了中间区向下坍塌的问题。
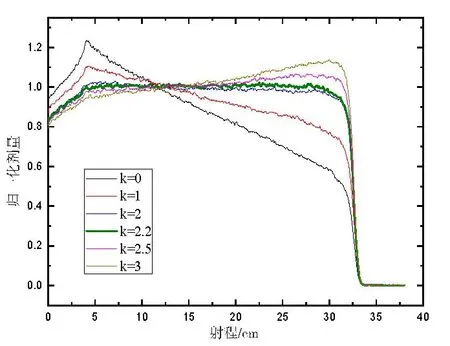
图5 不同k值的SOBP(4~32 cm)Fig.5 SOBP of 4-32cm with different k
对于不同深度和宽度的SOBP,重复上述过程即可得到平坦的SOBP,例如射程范围为10~16 cm的SOBP,如图6所示。各参数值α=447.912 7,P=1.769 3,a=4.493,b=-0.157,k=2。
2.2 横向剂量分布
以上讨论的两个区域SOBP对应的横向剂量分布如图7和图8所示,由于散射,质子束入射越深其横向分布偏离均匀分布越大,横向不再是尖锐的平台。临床上笔形束扫描能够得到纵向和横向均匀分布剂量,蒙特卡洛模拟则需要进一步考虑质子入射模式才能准确模拟横向均匀剂量。
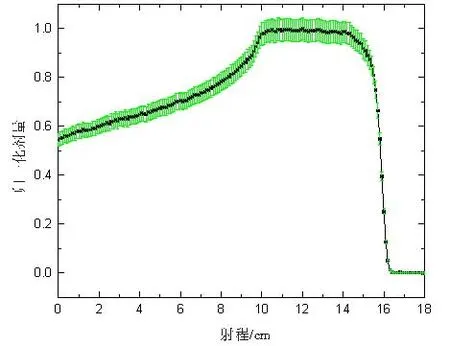
图6 k=2时10~16 cm的SOBPFig.6 SOBP of 10-16 cm with k=2
3 讨论
SOBP方法的本质是配置不同能量质子的权重,Bortfeld等利用拉普拉斯变换,从数学上解析求解了权重函数W(R),但根据该函数并不能得到平坦的SOBP,原因是解析解没有完全考虑粒子与物质的所有相互作用,尤其是散射效应。
利用蒙特卡洛模拟,F(R)弥补了散射等效应综合造成的影响,权重函数适配法可很快得到指定区间的SOBP,相比于前人的工作,虽然适配函数F(R)需要多拟合两个参数a和b,但解决了SOBP中间区下陷的问题。SOBP的形状对参数k比参数P更加敏感,有利工作人员快速判别。无论宽或窄的SOBP,FLUKA模拟验证了权重函数适配法的有效性。
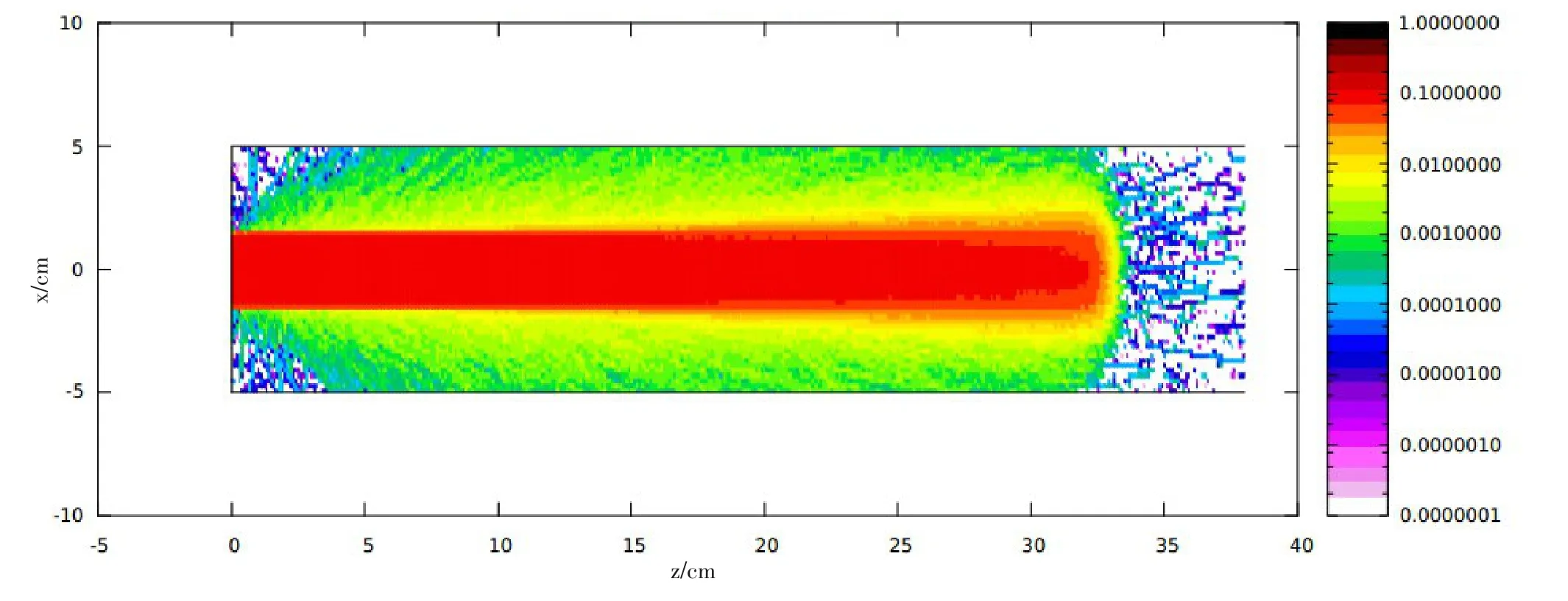
图7 横向剂量分布SOBP(4~32 cm)Fig.7 Lateral dose distribution of SOBP of 4-32 cm
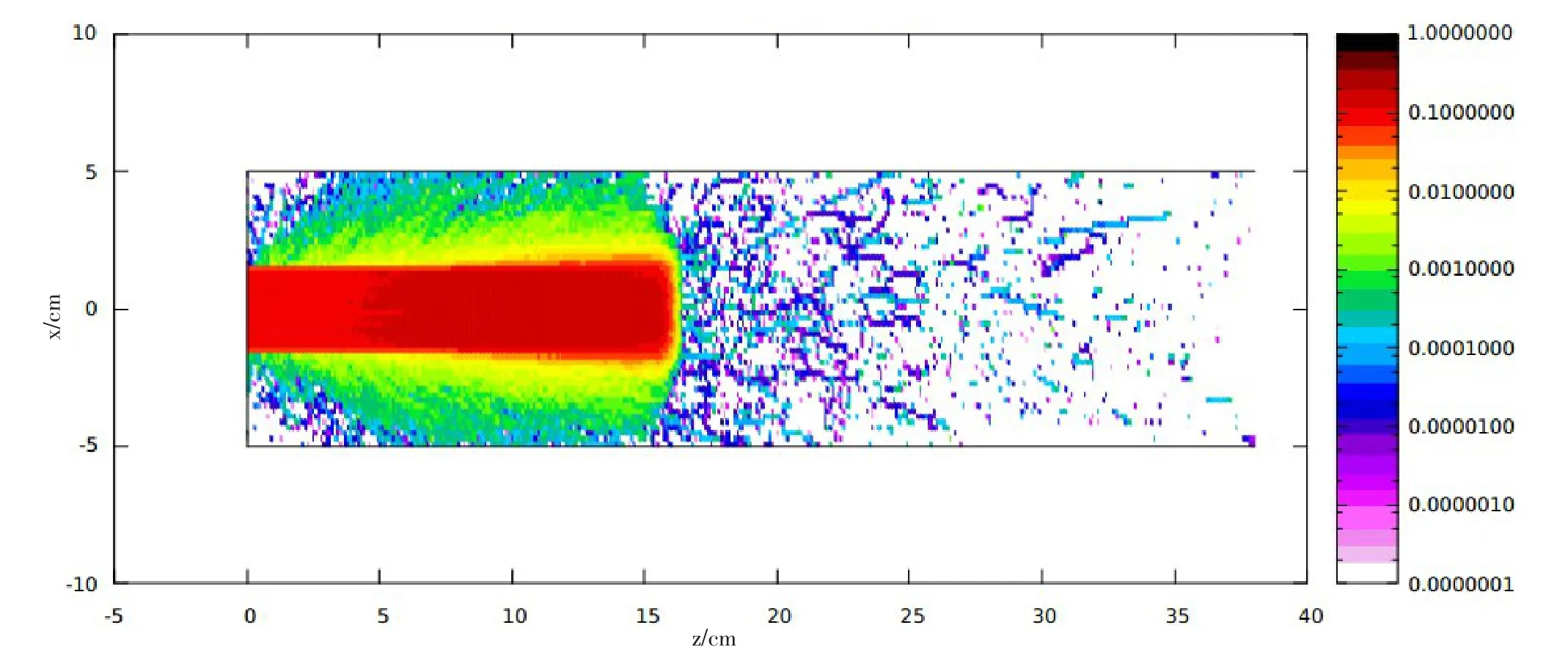
图8 横向剂量分布SOBP(10~16 cm)Fig.8 Lateral dose distribution of SOBP of 10-16 cm
权重函数适配法极具应用前景,可运用于质子重离子治疗计划中。但由于本文仅考虑了均匀面分布的平行入射质子束,其横向分布还有待深入探讨。
