光子与相对论麦克斯韦分布电子散射的能谱角度谱研究∗

李树

(北京应用物理与计算数学研究所,北京 100094)

(2018年9月30日收到;2018年11月5日收到修改稿)

光子与相对论麦克斯韦分布电子散射的描述及能谱角度谱计算非常复杂且费时.本文提出了一种光子与相对论麦克斯韦速度分布电子散射的蒙特卡罗(MC)模拟方法,该方法能够细致模拟高温等离子体中任意能量光子与任意温度电子的Compton和逆Compton散射问题.对于散射后光子的能谱和角度谱参数,可以根据电子温度抽样若干不同状态的电子,分别模拟其与光子发生散射,可以得到各次散射后的光子能量和偏转角度,取统计平均后的结果即可获得该光子与该温度电子散射的能谱和角度谱分布.根据该方法编写了光子与相对论电子散射MC模拟程序,开展了高温全电离等离子体中光子与相对论电子散射的能谱角度谱计算和分析,分析结果显示:热运动电子将展宽出射光子能谱,且低能光子与高温电子散射后的蓝移现象明显;出射光子的角度谱很复杂,其决定于入射光子能量、出射光子能量及电子温度.基于该方法计算并以数表形式给出的光子-相对论电子散射能谱角度谱数据,可以供辐射输运数值模拟程序使用.

1 引 言

1923年,美国物理学家A.H.Compton在研究X射线与物质散射的实验里发现,在被散射的X射线中,除了与入射X射线具有相同波长的成分外,还有波长增长的成分出现.增长的数量随散射偏转角的不同而不同,这是经典电磁理论无法解释的.Compton把观察到的现象理解为光子与自由电子碰撞的结果,用量子说给予了圆满的解释,证明了X射线的粒子性.光子与电子散射损失能量,波长变长,频率变低,称为Compton散射;光子与高能相对论电子散射获得能量,波长变短,频率变高,称为逆Compton散射[1].

光子与静止自由电子发生Compton散射后,出射光子能量与角度满足关系式:

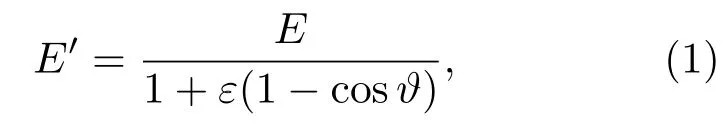
式中,E=hν是入射光子能量,E′=hν′是散射后出射光子能量;ε是入射光子能量与电子静止能量的比值,即ε=E/m0c2,m0是静止电子质量,c是光速;ϑ是入射光子与出射光子夹角(偏转角),故当偏转角为180◦时出射光子取最小能量[1]:

即出射光子的能量范围为[].

光子与静止自由电子发生Compton散射的能量微分截面可由Klein-Nishina(K-N)公式[2,3]给出:

式中,re是电子经典半径.

光子与运动自由电子发生散射时,存在所谓的“红移”,“蓝移”及“多普勒展宽”现象[4],使得散射后光子的能谱分布发生变化.

在恒星内部、惯性约束聚变区、热核装置等温度高达亿度的等离子体系统中,光子与高速热运动电子发生Compton散射和逆Compton散射.如果电子处于热平衡态,其速率服从相对论麦克斯韦-玻尔兹曼(relativistic Maxwellian Boltzman,RMB)分布[4,5].已有多篇文献[6-18]介绍了如何计算光子与RMB电子散射总截面及散射能量微分截面、散射角度微分截面,这些文献采用的方法均是多重数值积分方法.

利用隐式蒙特卡罗(implicit monte carlo,IMC)方法[19,20]模拟高温等离子体中的辐射输运问题时,需要知道任意能量的光子与任意温度电子的相互作用(吸收、散射)截面以及发生散射后出射光子的能量和角度.文献[21]中介绍了光子与相对论电子散射截面的蒙特卡罗(MC)计算方法,本文介绍如何确定散射后光子的能量和方向,同时利用本方法计算给出一些典型情况下散射后光子的能量微分截面及能量-角度双微分截面,分析研究微分散射截面变化规律.

2 光子与相对论电子散射的蒙特卡罗模拟方法

如图1所示,设实验室坐标系X0Y0Z0(简称0系)中,t时刻有一光子(hν0,Ω0)(光子能量和飞行方向),求其与r0处温度为Te的电子发生散射的概率(微观散射截面)及散射后光子的能量、角度分布.在文献[21]中已讨论了散射概率的计算方法,本文讨论散射后光子的能量、角度计算方法以及能谱和角度谱分布计算方法.

MC求解步骤如下.

第1步,在实验室坐标系中抽样出单个相对论麦克斯韦电子的方向和速率,如图2所示.

第2步,在实验室坐标系的基础上,经旋转和平移后建立X1轴正方向与电子运动方向Ω0e一致的新坐标系1,将光子和电子的状态转换到坐标系1中.

第3步,在坐标系1的基础上,建立随电子运动的坐标系2,经Lorentz变换,将光子的状态转换到坐标系2中;

第4步,在坐标系2的基础上,以Z2轴为旋转轴旋转α2角度,建立新的坐标系3;光子和电子在3系中相互作用的物理图像是,一个能量为hν3的光子沿X3轴正方向飞行,在坐标原点处与一个自由静止的电子发生散射,如图3所示.

图1 实验室系光子与温度为Te的电子散射示意图Fig.1.A photon scattering with electrons at temperature in lab coordinate.

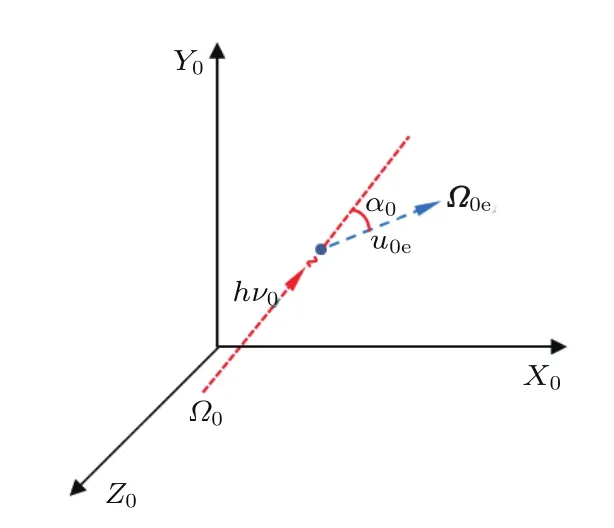
图2 实验室系光子与抽样出的单个电子散射前示意图Fig.2.A photon scattering with the sampled electron in lab coordinate.

图3 坐标系3中光子与电子散射示意图Fig.3.A photon scattering with a electron in coordinate 3.

上述4个步骤的详细处理过程请参考文献[21].

光子与自由静止电子发生Compton散射采用K-N公式处理,可以计算出光子(hν0,Ω0)与相对论电子(u0e,Ω0e)发生散射的概率σs(ε)[21].有各种办法和程序用来抽样处理散射后光子的能量和方向[22].目前比较常用的方法是:对于入射能量不超过1.4 MeV的光子,采用Kahn方法[23]抽样出射光子能量和方向(偏转角度);对于入射能量超过1.4 MeV的光子,采用Koblinger方法[24]抽样出射光子能量和方向(偏转角度).这也是本文采用的处理方法.

第5步,采用Kahn和Koblinger方法,我们可以得到散射后光子的能量以及偏转角ϑ.另外,出射光子的方向角φ由抽样φ=2πξ得到,如图3所示.由此可得在坐标系3中散射后的光子状态(,):

第6步,求3系中的光子(,)在2系中的状态(,).由于2系与3系之间只存在以Z轴为旋转轴、转角为α2的(二维)旋转变换,故光子频率不变=,两个坐标系间光子飞行方向有如下关系:

代入第3步中已经求得的sinα2和cosα2值以及第5步抽样得到光子频率和方向值之后,得到散射后光子在2系中的四度向量

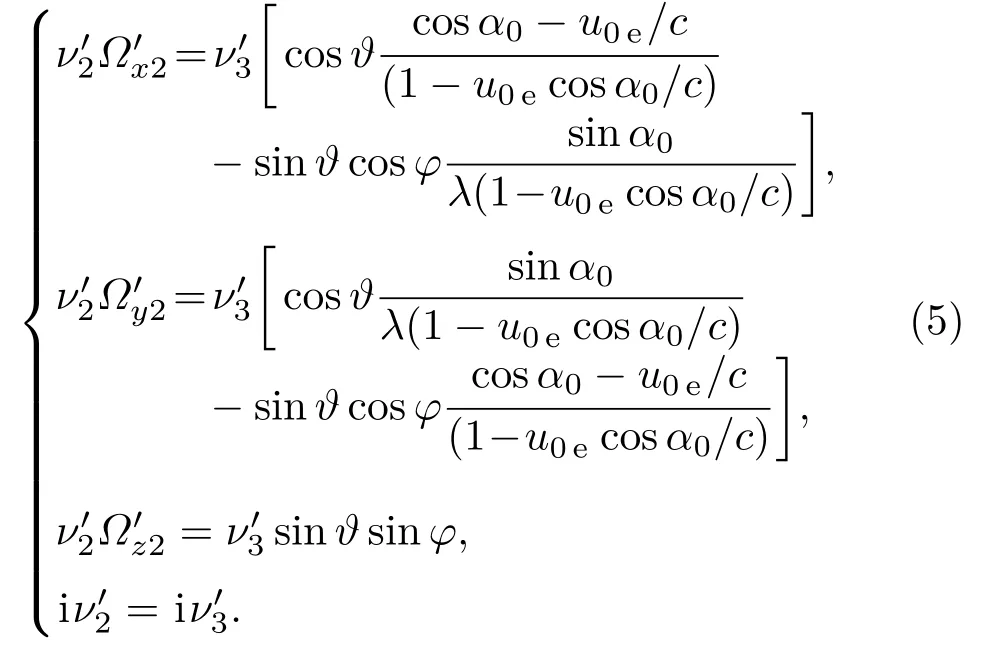
第7步,求2系中的光子(,)在1系中的状态(,).从前面的第3步知道,坐标系2是相对于坐标系1以速率u0e运动的坐标系.根据狭义相对论,1系中的光子四度向量可通过逆向的Lorentz变换[25]得到:

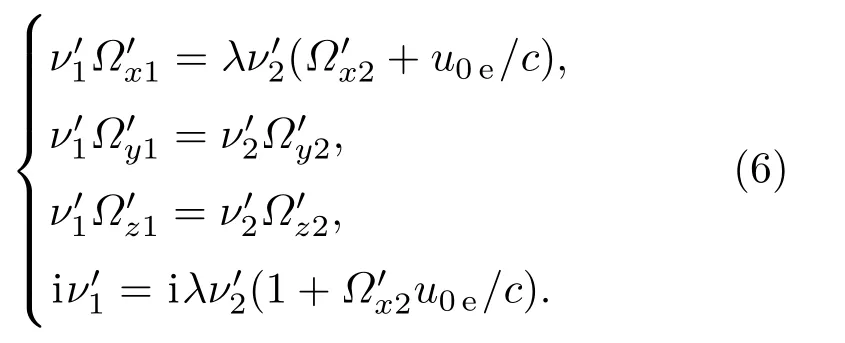
式中,λ是Lorentz因子λ=[1-(u0e/c)2]-1/2.代入根据(5)式求得的及(,,)后即得到光子在1系中的状态(,).

第8步,再做1次(三维)旋转变换[26],将散射后光子在1系中的状态(,)转换成在实验室坐标系(0系)中的状态(,).根据第2步的坐标系1建立过程,可以得到1系与0系中的光子飞行方向矢量满足如下关系:

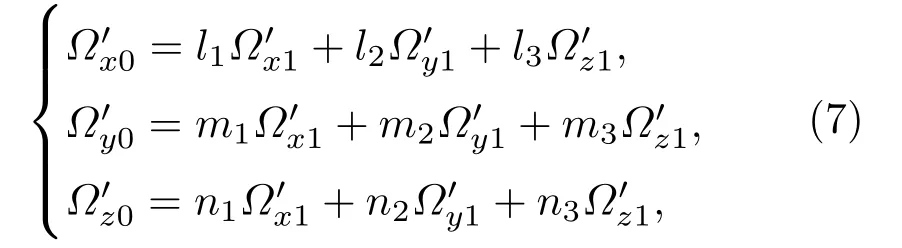
式中,

又因为1系与0系只存在平移和旋转变换,矢量长度不变,因此光子频率=.至此,求得了光子(hν0,Ω0)与电子(u0e,Ω0e)散射后的光子在实验室坐标系中的状态(,).

最后归纳MC模拟的8个步骤包含:2次抽样(1次RMB抽样、1次K-N公式抽样);2次二维(平面)旋转变换;2次三维(空间)旋转变换;2次Lorentz变换.前3次坐标变换(步骤2,3,4)的目的是:将实验室系中“任意能量和运动方向的光子”与“任意速度、任意位置的自由电子”之间的散射变换成“变换后相应能量并沿X轴正方向飞行的光子”与“静止于坐标系原点处的电子”之间的散射,在此基础上方可采用K-N公式方便地处理光子与电子散射问题(步骤5).后3次坐标变换(步骤6,7,8)的目的是将散射后光子的能量和方向由电子静止坐标系还原回初始的实验室坐标系,是步骤2至步骤4的逆过程.

上面的8个步骤描述了入射光子(hν0,Ω0)与单个特定(根据电子温度Te抽样出的)相对论电子发生散射后光子状态的MC计算方法.根据上述步骤编制MC程序,即可细致模拟高温等离子体中任意能量光子与任意温度电子的Compton和逆Compton散射问题.

利用确定论方法(SN,PN)模拟高温等离子体中的辐射输运问题时,需要知道某能群的光子与某温度的电子散射后的能群转移概率及离散方向转移概率(双微分截面),即需要事先制备好光子与电子散射的能谱及能量-角度联合谱参数.

对于光子(hν0,Ω0)与温度为Te的电子发生散射后的能谱及能量-角度联合谱参数,我们也可以利用本方法制备.重复步骤1—8若干(N)次,统计出射光子的能量和角度分布,取N次平均的结果:

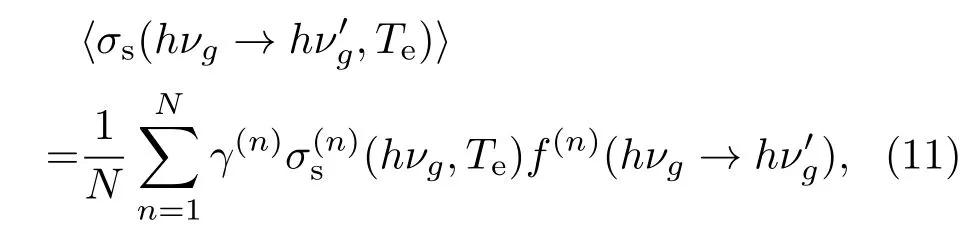
式中,hνg是第g群入射光子的平均能量;(hνg,Te)是MC模拟第n个样本在第4步计算得到的散射截面,γ(n)是第n次抽样计算的空间变化Lorentz因子:

式中,cosα0=Ω0·Ω0e是光子与电子的飞行方向夹角余弦.

(11)式中,f(n)(hνg→)是模拟第n个样本的出射光子能量(即第8步得到的)落在第g′群的概率,如果是则为1,否则为0.由此,通过MC方法计算得到光子-相对论麦克斯韦电子散射的光子能谱分布(统计平均的第g群能量微分散射截面⟨σs(hνg→,Te)⟩).

同理,对于能量-角度联合谱分布,可以通过如下公式计算得到:

式中,l是角度区间标识,g(µl)是MC模拟第n个样本的出射光子偏转角度µl落在第l角度区间的概率,如果是则为1,否则为0.得到统计平均的第g群、第l角度区间的能量-角度双微分散射截面

3 散射光子能谱角度谱的数值模拟结果与分析

只要电子速率分布抽样及K-N公式抽样方法足够准确以及抽样的样本数N足够多,本方法计算得到的光子与相对论电子散射后的光子能谱分布以及能量-角度联合谱分布便足够精确.针对这三个影响计算精度的问题,这里需要指出:1)第1步中,电子速率的抽样是本方法目前已知的影响计算精度的主要因素,正如文献[21]中已探讨的,在电子温度不超过25 keV情况下,本方法目前的电子速率抽样精度足够高,但是在电子温度更高的情况下,电子速率抽样结果偏低,这也势必影响散射后光子的能谱角度谱分布;2)第5步中,本文采用了非常成熟的K-N公式抽样方法来确定光子与静止电子散射后的能量和方向,且作者也做了细致的分析,确认其抽样精度是非常高的(见图4,图7,图10);3)本文后面的数据均是采用了非常大(1亿)样本量的数值模拟结果,绝大多数数据的统计误差均非常小,可以认为结果已经收敛,因此将不讨论由MC方法模拟的统计噪声而引起的计算误差问题.总之,目前本方法及后面所列的计算结果中,对于电子温度小于25 keV的情况,计算精度高、模拟结果可靠;对于温度更高的情况,误差稍大,请读者谨慎对待.

根据本文第2节介绍的方法,研制了光子-相对论麦克斯韦电子散射模拟程序,该程序可以计算任意光子(能量范围[0—1 MeV])与任意温度电子(温度范围[0—100 keV])的微观散射截面及能谱、能量-角度联合谱.本文利用该程序模拟了若干能量入射光子与若干温度电子散射问题,统计计算对应的能量微分截面及能量-角度双微分截面,并开展分析研究.

首先分析研究光子与相对论电子散射的能谱.表1是不同能量入射光子与不同温度电子散射后的平均出射光子能量;表2,表3分别是对应的红移和蓝移份额;其中,红移份额定义为出射光子能量(实验室坐标系)低于的百分比;蓝移份额定义为出射光子能量(实验室坐标系)高于hν0的百分比.

分析表1数据,电子静止(温度0 keV)情况下,光子通过Compton散射净损失能量,出射光子能量不高于入射光子;热运动电子(温度非0)使得出射光子平均能量增加,电子温度越高,出射光子平均能量越大.

分析表2和表3,电子静止情况下,本方法模拟的出射光子能量不超出范围[,hν0)];由于电子热运动导致的多普勒效应和逆Compton效应,使得出射光子能量发生了红移()和蓝移(0);入射光子能量越低,红移和蓝移份额越大,例如对于较低入射能量光子(<1 keV),绝大部分出射光子的能量没有在[,hν0)]范围之内;电子温度越高,逆Compton效应越显著,蓝移份额越大.

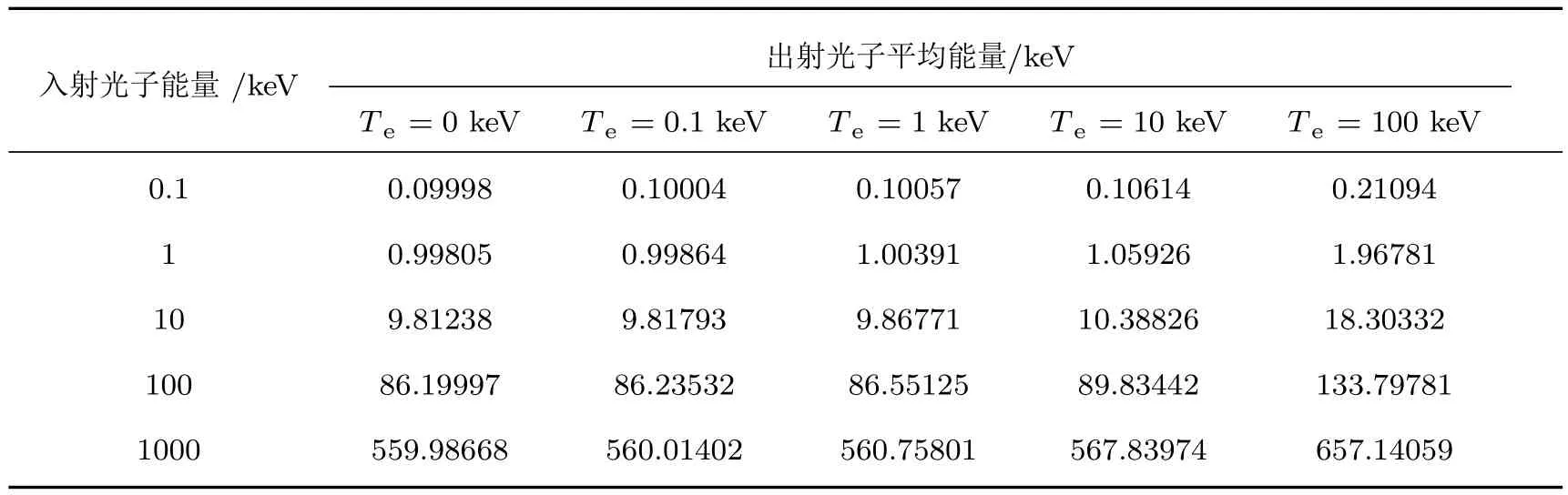
表1 光子-相对论麦克斯韦电子散射的出射光子平均能量Table 1.Averaged energy of the final photon of photon-Maxwellian electron scattering.

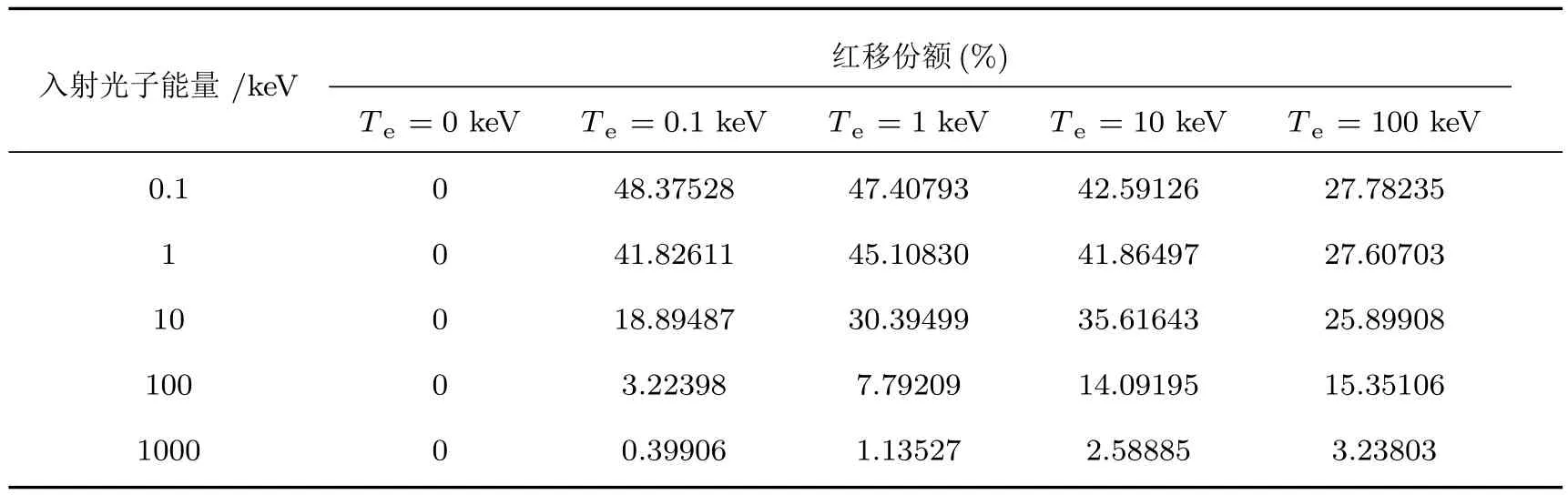
表2 光子-相对论麦克斯韦电子散射的红移份额Table 2.Percent of red shift of photon-Maxwellian electron scattering.

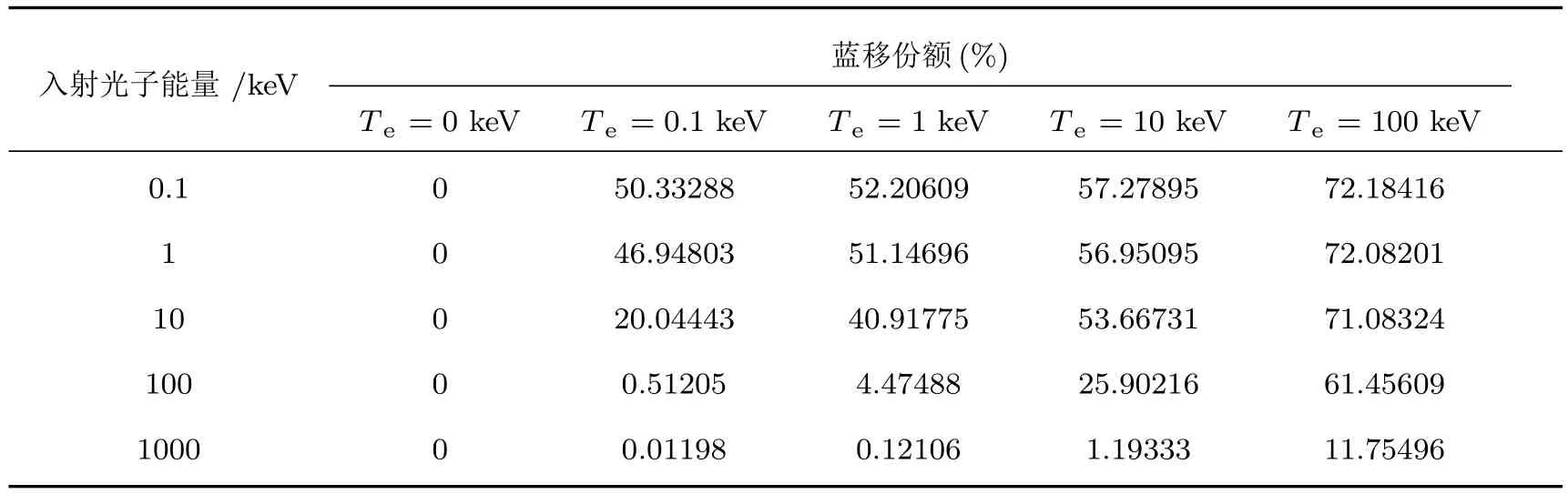
表3 光子-相对论麦克斯韦电子散射的蓝移份额Table 3.Percent of blue shift of photon-Maxwellian electron scattering.

图4—图6分别是入射能量为0.1 keV光子与温度为0,1,100 keV的电子发生散射后,出射光子的能量微分截面分布(未归一的能谱);其中,图4还给出了本方法计算结果与Kahn抽样方法计算结果、K-N公式解析计算结果的比较情况.

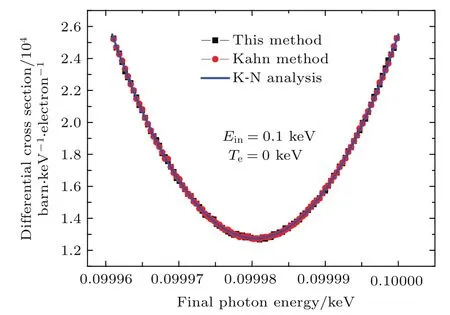
图4 散射光子能量微分截面分布及与K-N公式解析结果比较(Ein=0.1 keV,Te=0 keV)Fig.4.The differential scattering cross sections dσs/dE and vs.K-N analysis(Ein=0.1 keV,Te=0 keV).

图5 散射光子能量微分截面分布(Ein=0.1 keV,Te=1 keV)Fig.5. The differential scattering cross sections dσs/dE(Ein=0.1 keV,Te=1 keV).

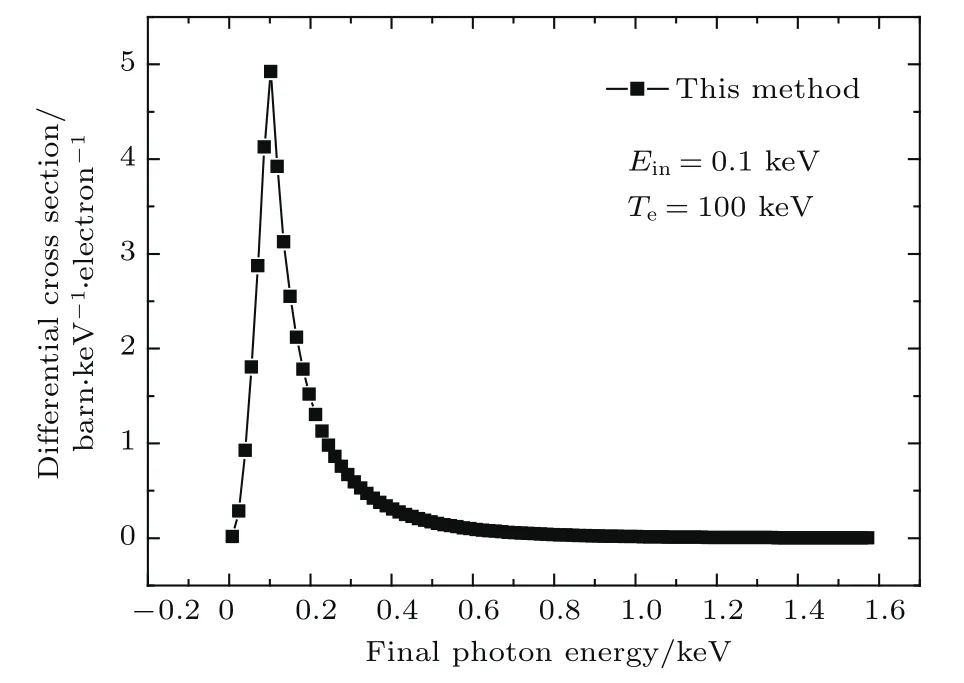
图6 散射光子能量微分截面分布(Ein=0.1 keV,Te=100 keV)Fig.6. The differential scattering cross sections dσs/dE(Ein=0.1 keV,Te=100 keV).

图7—9分别是入射能量为10 keV光子与温度为0,1,100 keV的电子发生散射后,出射光子的能量微分截面分布;其中,图7还给出了本方法计算结果与Kahn抽样方法计算结果、K-N公式解析计算结果的比较情况.

图7 散射光子能量微分截面分布及与K-N公式解析结果比较(Ein=10 keV,Te=0 keV)Fig.7.The differential scattering cross sections dσs/dE and vs.K-N analysis(Ein=10 keV,Te=0 keV).

图8 散射光子能量微分截面分布(Ein=10 keV,Te=1 keV)Fig.8. The differential scattering cross sections dσs/dE(Ein=10 keV,Te=1 keV).

图9 散射光子能量微分截面分布(Ein=10 keV,Te=100 keV)Fig.9.The differential scattering cross sections dσs/dE(Ein=10 keV,Te=100 keV).

图10—12分别是入射能量为1000 keV光子与温度为0,1,100 keV的电子发生散射后,出射光子的能量微分截面分布;其中,图10还给出了本方法计算结果与Kahn抽样方法计算结果、K-N公式解析计算结果的比较情况.

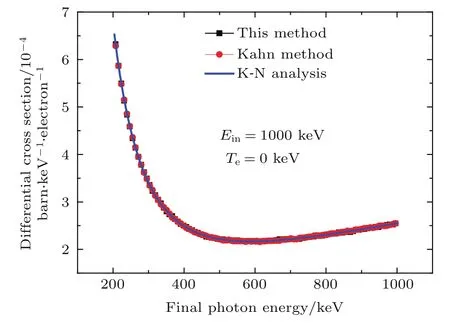
图10 散射光子能量微分截面分布及与K-N公式解析结果比较(Ein=1000 keV,Te=0 keV)Fig.10.The differential scattering cross sections dσs/dE and vs.K-N analysis(Ein=1000 keV,Te=0 keV).

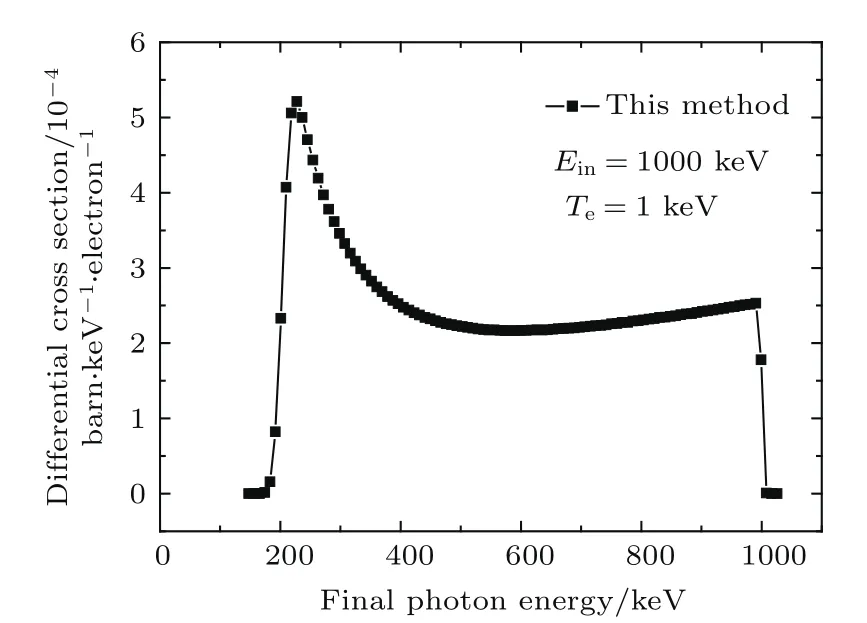
图11 散射光子能量微分截面分布(Ein= 1000 keV,Te=1 keV)Fig.11.The differential scattering cross sections dσs/dE(Ein=1000 keV,Te=1 keV).

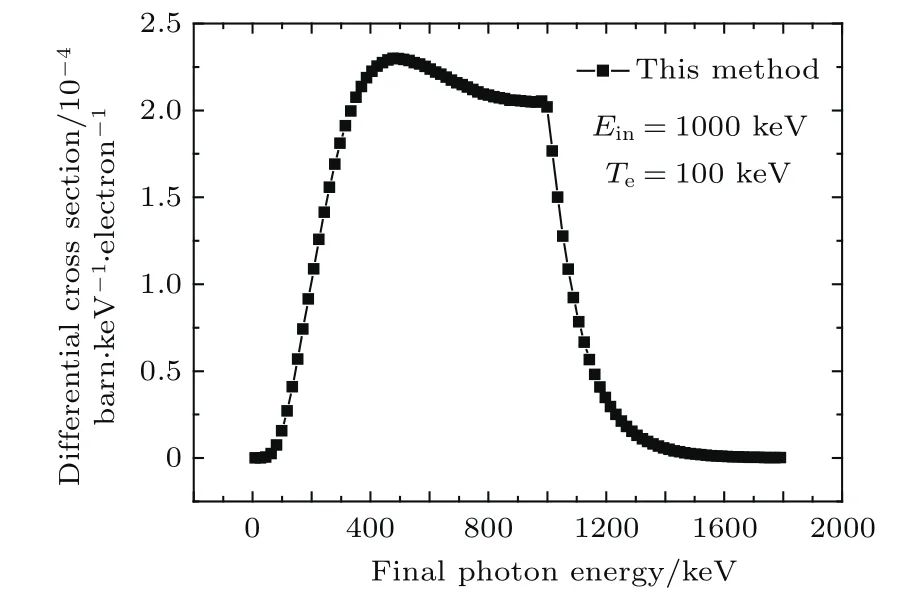
图12 散射光子能量微分截面分布(Ein= 1000 keV,Te=100 keV)Fig.12.The differential scattering cross sections dσs/dE(Ein=1000 keV,Te=100 keV).

分析图4—图12的数据:

在不考虑电子热运动情况下(Te=0 keV),从图4、图7、图10的比较中可知本方法结果与Kahn抽样方法及K-N公式解析结果一致;

在不考虑电子热运动情况下,对于低能入射光子(图4),出射光子能量分布在非常窄的范围之内,可以近似认为光子能量没有发生变化,即可将低能光子与静止电子的散射退化为Thomson散射;随着入射光子能量增加(图7,图10),出射光子能量分布变宽,因此用Thomson散射近似所带来的误差也会逐渐增大;

电子温度非0与电子温度为0的能谱图比较可以看出:电子热运动将展宽出射光子能谱,电子温度越高,出射光子能谱展宽越显著;考虑电子热运动后,即时是低能入射光子(图5,图6),采用Thomson散射近似也是不合适的;

当电子温度与入射光子能量相比较低或相当时(图8,图11,图12),能谱主要体现为多普勒展宽;当电子温度与入射光子能量相比较高时(图6,图9),逆Compton散射效应使得很多出射光子能量增加,蓝移现象很显著,且电子温度越高,蓝移份额越大.

接下来分析研究光子与相对论电子散射的角度谱.图13是利用(1)式计算给出的入射能量为0.1 keV光子与静止自由电子散射后出射光子能量-角度关系;图14—图16分别是本方法计算给出的入射能量为0.1 keV光子与温度为0,1,100 keV的电子发生散射后,出射光子的能量-角度双微分截面分布图.

图13 散射光子能量-角度关系(Ein=0.1 keV,Te=0 keV)Fig.13.The relationship between energy and angle of the final photon(Ein=0.1 keV,Te=0 keV).

图14 散射光子能量-角度双微分截面分布(Ein=0.1 keV,Te=0 keV)Fig.14.The double differential scattering cross sections dσs/dE/dϑ (Ein=0.1 keV,Te=0 keV).

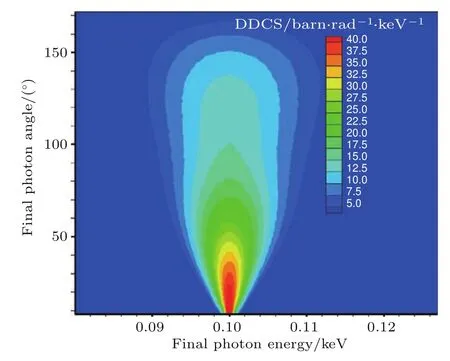
图15 散射光子能量-角度双微分截面分布(Ein=0.1 keV,Te=1 keV)Fig.15.The double differential scattering cross sections dσs/dE/dϑ (Ein=0.1 keV,Te=1 keV).

图16 散射光子能量-角度双微分截面分布(Ein=0.1 keV,Te=100 keV)Fig.16.The double differential scattering cross sections dσs/dE/dϑ (Ein=0.1 keV,Te=100 keV).

图17 是利用(1)式计算给出的入射能量为10 keV光子与静止自由电子散射后出射光子能量-角度关系;图18—图20分别是本方法计算给出的入射能量为10 keV光子与温度为0,1,100 keV的电子发生散射后,出射光子的能量-角度双微分截面分布图.

图21是利用(1)式计算给出的入射能量为1000 keV光子与静止自由电子散射后出射光子能量-角度关系;图22—图24分别是本方法计算给出的入射能量为1000 keV光子与温度为0,1,100 keV的电子发生散射后,出射光子的能量-角度双微分截面分布图.

图17 散射光子能量-角度关系(Ein=10 keV,Te=0 keV)Fig.17.The relationship between energy and angle of the final photon(Ein=10 keV,Te=0 keV).

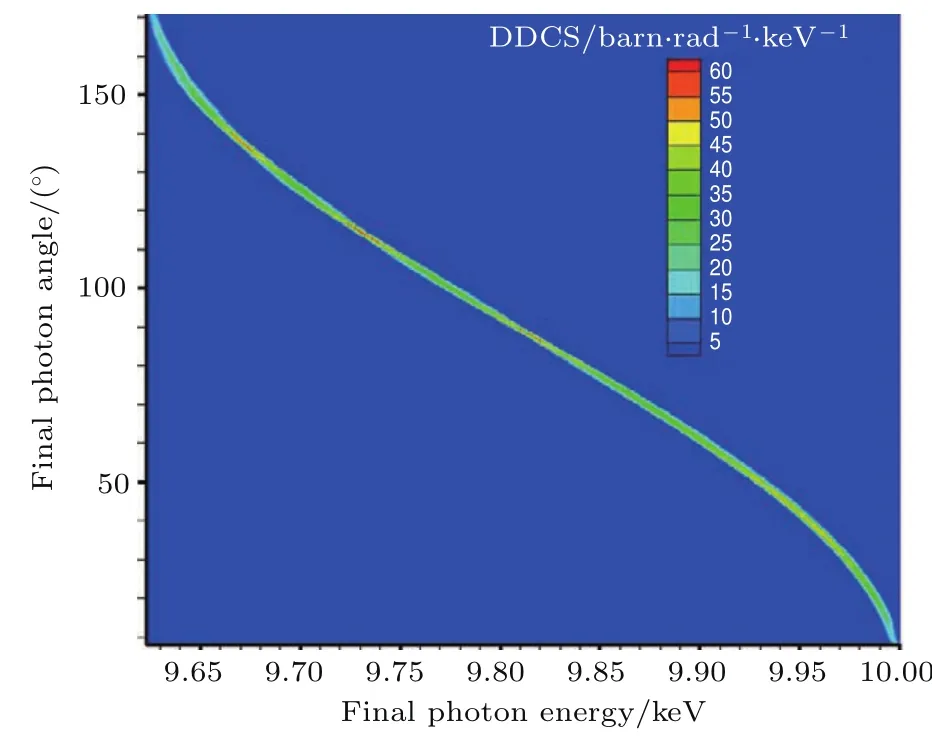
图18 散射光子能量-角度双微分截面分布(Ein=10 keV,Te=0 keV)Fig.18.The double differential scattering cross sections dσs/dE/dϑ (Ein=10 keV,Te=0 keV).

图19 散射光子能量-角度双微分截面分布(Ein=10 keV,Te=1 keV)Fig.19.The double differential scattering cross sections dσs/dE/dϑ (Ein=10 keV,Te=1 keV).

图20 散射光子能量-角度双微分截面分布(Ein=10 keV,Te=100 keV)Fig.20.The double differential scattering cross sections dσs/dE/dϑ (Ein=10 keV,Te=100 keV).

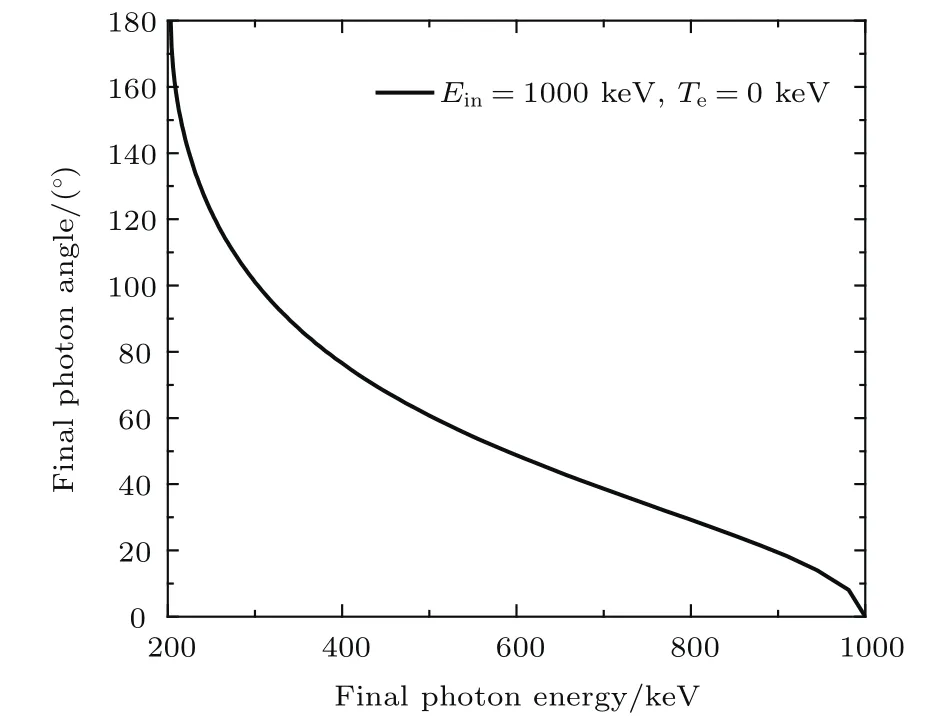
图21 散射光子能量-角度关系(Ein=1000 keV,Te=0 keV)Fig.21.The relationship between energy and angle of the final photon(Ein=1000 keV,Te=0 keV).

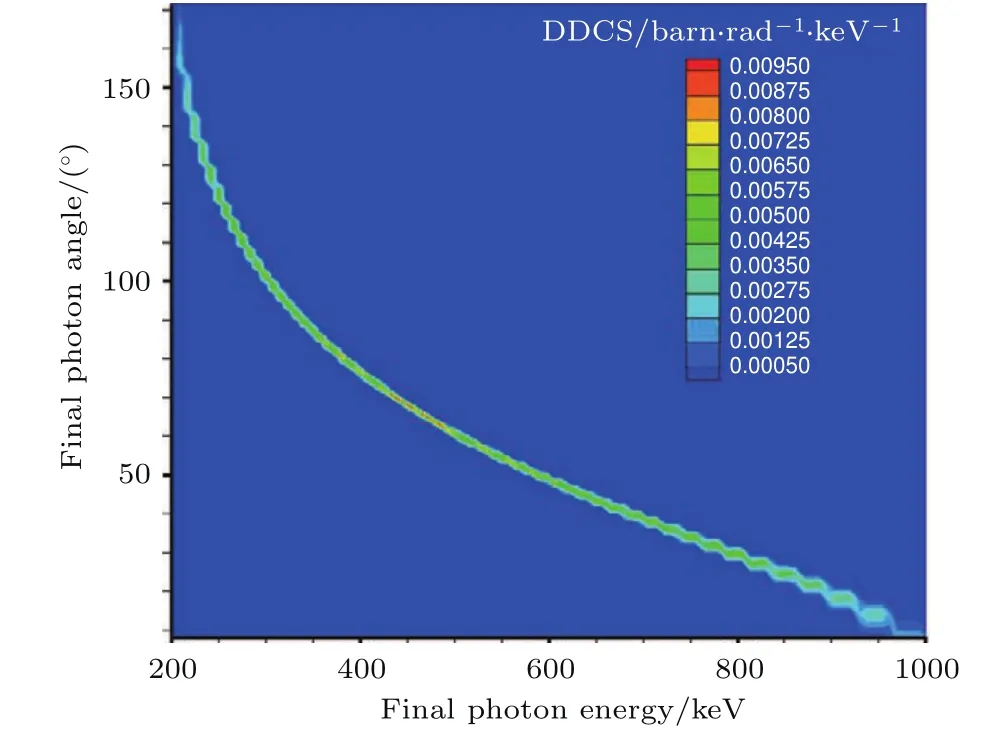
图22 散射光子能量-角度双微分截面分布(Ein=1000 keV,Te=0 keV)Fig.22.The double differential scattering cross sections dσs/dE/dϑ (Ein=1000 keV,Te=0 keV).

图23 散射光子能量-角度双微分截面分布(Ein=1000 keV,Te=1 keV)Fig.23.The double differential scattering cross sections dσs/dE/dϑ (Ein=1000 keV,Te=1 keV).

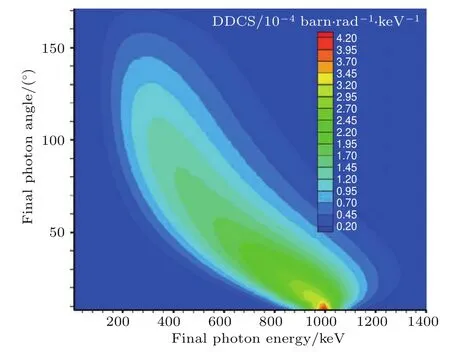
图24 散射光子能量-角度双微分截面分布(Ein=1000 keV,Te=100 keV)Fig.24.The double differential scattering cross sections dσs/dE/dϑ (Ein=1000 keV,Te=100 keV).

在电子0温情况下,从图13与图14、图17与图18、图21与图22比较结果可以看出,本方法计算结果与解析结果基本一致.需要指出的是,本方法的计算结果图像(图14,图18,图22)中,对于确定的单一出射能量光子,角度并不是单一的值,而是有一个窄小的宽度分布,这是MC方法统计时需要将光子能量分群、光子角度分间隔所导致的,这并不会影响主要的物理认识.

考虑电子热运动后,出射光子的角度与能量不再是单一函数关系((1)式),而是有一定的概率分布,此概率的分布与入射光子能量、电子温度及出射光子能量相关.总体来看,出射光子能量与入射光子能量较接近时,出射光子的角度主要分布在小角度附近(向前飞行);随着出射光子能量逐渐偏离入射光子能量,其角度分布也逐渐向大角度发展;随着电子温度升高,出射光子能量-角度联合谱逐渐展宽,且主要是向高能-大角度方向发展.

总之,光子与相对论电子散射的能量微分截面及能量-角度双微分截面比较复杂,很难给出解析计算公式或者近似拟合公式.因此,在实际应用中,比较可行的办法是:根据问题性质,利用本方法(或其他方法)首先计算出若干能量入射光子与若干温度电子散射的能量微分截面及能量-角度双微分截面值,并以离散数表的形式将这些数值存储起来,然后在计算具体问题时根据情况进行插值,最后得到所需的能量微分截面及能量-角度双微分截面.

4 结 论

本文提出了一种光子与相对论麦克斯韦分布电子散射的能量微分截面及能量-角度双微分截面的蒙特卡罗数值模拟计算方法.本方法的MC模拟包含8个步骤:2次抽样(1次RMB抽样、1次K-N公式抽样),2次二维(平面)旋转变换,2次三维(空间)旋转变换,2次Lorentz变换.根据上述步骤编制MC程序,即可细致模拟高温等离子体中任意能量光子与任意温度电子的Compton和逆Compton散射问题.另一方面,通过重复抽样若干样本并完成每个样本的8个步骤模拟,取所有样本模拟结果的统计平均值后,即可获得某确定能量的入射光子与某确定温度的电子发生散射后,出射光子的能谱分布及能量-角度联合谱分布或者对应的微分截面数据.这些截面数据可以供其他确定论辐射输运数值模拟程序使用,或者用于其他高温等离子中光子与电子相互作用问题的研究中.

考虑电子热运动后,数值模拟结果分析显示:出射光子的能谱主要体现为多普勒展宽和蓝移现象,具体情况与入射光子能量及电子温度相关;出射光子的角度与能量不再是单一函数关系,而是有一定的概率分布,此概率的分布与入射光子能量、电子温度及出射光子能量相关,形式比较复杂,但可以利用本方法计算并以数表形式给出需要的参数.