三维各向同性谐振子的几何动量分布∗

刘全慧 张梦男 肖世发2) 寻大毛1

)(湖南大学物理与微电子科学学院,理论物理研究所,长沙 410082)

2)(岭南师范学院物理科学与技术学院,湛江 524048)

3)(江西科技师范大学通信与电子学院,南昌 330013)

(2018年9月3日收到;2018年11月6日收到修改稿)

尽管几何动量最初的引入是为了描述超面上的运动粒子的动量,却不需要限制在真实的曲面上.如果一个曲线坐标系包含了超面族和超面上的法向矢量作为一个坐标轴的单位矢量,几何动量可以定义在超面族上,并参与构造对易力学量完全集.在三维各向同性谐振子中,采用球坐标描述,存在等效球面,并在球面族上建立对易力学量完全集.因此,三维各向同性谐振子同时具有动量和几何动量分布.这两个动量的差,可以定义为径向动量,从而使得径向动量可以测量.那么,通过几何动量,可以显示出狄拉克引进的径向动量的物理意义,而不是一直认为的那样完全不具有观测意义.

1 引 言

为了恰当地描述约束在超曲面上粒子的量子运动,2011年正式引入了几何动量[1],2015年几何动量获得实验的验证[2].如何把这一动量纳入到狄拉克正则量子化的框架之中,2012年至2018年间进行了一系列的探索[3-12],2018年这一问题获得解决[11,12].

几何动量、几何势能等几何量[1,3,9,10]可以循如下步骤而获得.把几何面想象成有均匀厚度的一个薄层,如果在这个薄层中定义动量,然后让薄层的厚度趋于零,在经典力学中,和直接在曲面上定义动量完全一样.但是,在量子力学,情况则完全不同.首先需要在这个薄层中写下薛定谔方程,然后让薄层的厚度趋于零,则薛定谔方程分离成两个独立的部分,一个沿曲面法向方向的方程,一个沿曲面切向方向的方程.法向方向的运动,由于自由度冻结,仅仅处在基态上.这时可以发现切向运动的微分算符会多出依赖于曲率的项,例如动量由-i变为如下算符pΣ,动能算符-2∇2/(2µ)→-2∇2LB/(2µ)+Vg,

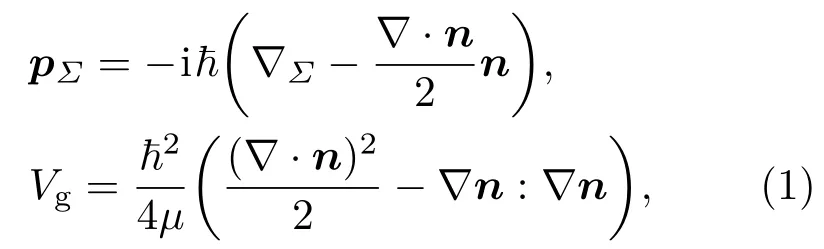
其中n为超曲面上的单位法矢量,梯度算符∇定义在超曲面所嵌的平直空间中,∇Σ为曲面上的梯度算符,∇2LB为曲面上的Laplace-Beltrami算符.因为在任意维的超曲面上,-∇·n定义为曲面的平均曲率,几何势能也依赖于平均曲率,所以(1)式中的算符pΣ称之为几何动量,Vg称之为几何势能.这样定义的几何动量、几何势能不因曲面上参数的改变而改变,都是几何不变量.很容易想到,任何包含几何动量和Laplace-Betrami算符及其幂次的力学量,都将出现依赖平均曲率的项[9,10].

从引入动量的过程可以看出,动量可以不必建立在真实的曲面上.设超面为N维,曲面的附近有一点,则这一点的位置可以按如下两种方式决定下来.第一种方式很简单,就是在曲面的高一维的平直空间中,直接用直角坐标描述,即r=(x1,x2,···,xN+1).第二种方式就是采用所谓的高斯法向坐标,即N个坐标为曲面内的坐标参数,不妨设为(α1,α2,···,αN),第N+1个坐标取在曲面的法线方向上,不妨设为β.毫无疑问,这两种方法完全等价,即二者之间可以进行坐标变换,

其中α为N个曲面中的坐标(α1,α2,···,αN)的简写.把梯度算符写在高斯法向坐标中,即

注意到N+1维平直空间中的动量算符的定义为p=-i,每个分量都可以测量.从高斯法向坐标中法向分量的角度看,动量的这个分量-i必须厄米化,即法向的动量是

于是

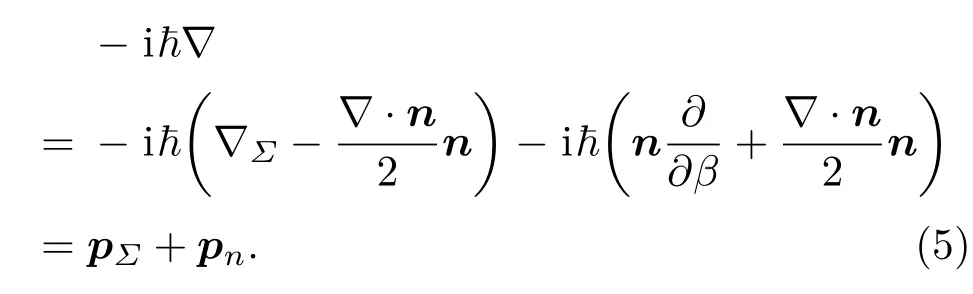
对于N维的超球面,

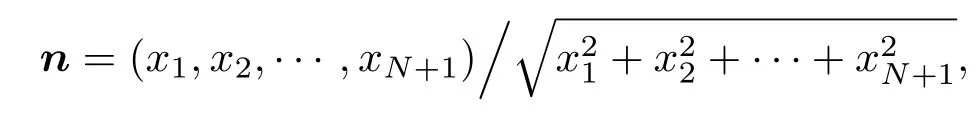
由于

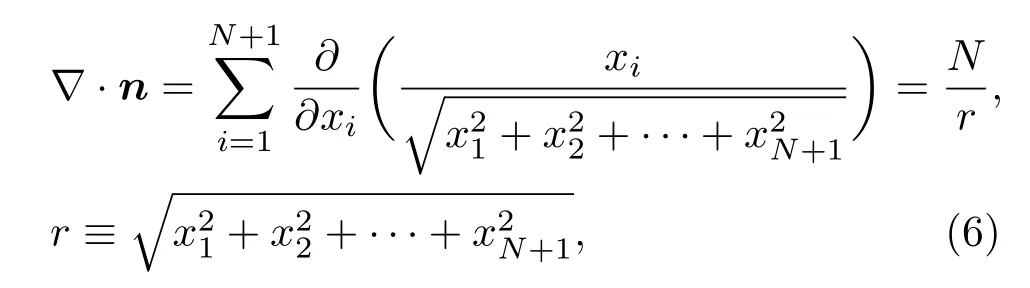
即可得(5)式中的第二部分即法向动量,也就是所谓的径向动量[13],

对于二维球面N=2,pr=-i(∂r+1/r)n.

众所周知,径向动量不是数学上的自伴算符,故“没有观测意义”[14-16].但是,狄拉克坚持认为这是一个有意义的量子力学算符,却没有说明测量它的具体方案[13].注意到(5)式中的第一部分即所谓的几何动量,它是自伴算符.为什么(5)式中左边的算符是自伴算符,右边的两个算符一个自伴一个不自伴?这是可能的,因为三个算符各自作用的空间不同.(5)式提示出法向动量可以定义等效算符

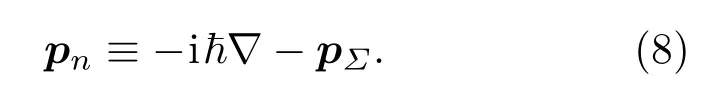
利用这一等效算符,就可以解决法向动量不具有自伴性却可以计算出不确定度这二者之间的矛盾[17],另外还发现了几何动量在磁单极-电荷系统中和几何相位之间的联系[18].本文利用三维各向同性谐振子系统,通过动量和几何动量之间的关系,继续考察径向动量可测量性等问题.

本文第2节建立三维各向同性谐振子的动量和几何动量的分布普遍理论,第3节是具体计算结果,第4节是总结.

2 三维各向同性谐振子的动量和几何动量的分布普遍理论

2.1 几何动量和包含几何动量的力学量完备集

在三维直角坐标系中,几何动量pΣ的三个分量的明显形式是

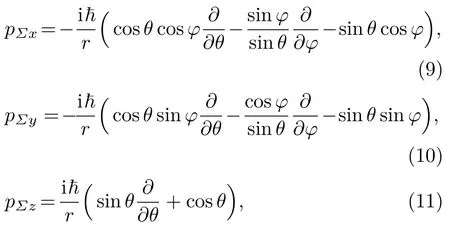
每个分量都有完备的本征函数和本征值[3,19].注意到轨道角动量在直角坐标系的三个分量为

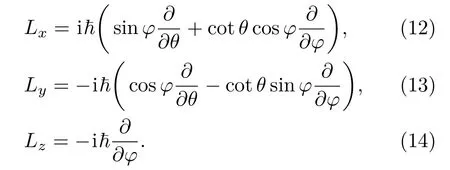
这两组力学量都不包含对径向位置的微分,它们之间的任意一个都可以和径向位置算符同时对角化.因此,可以选径向位置算符取某个确定值的表象中进行研究三维各向同性谐振子.取径向位置为某个定值,设为r,这时就等效于在某个等效球面上研究这个问题.

不难验证角动量与几何动量的分量的对易关系满足SO(3,1)代数,

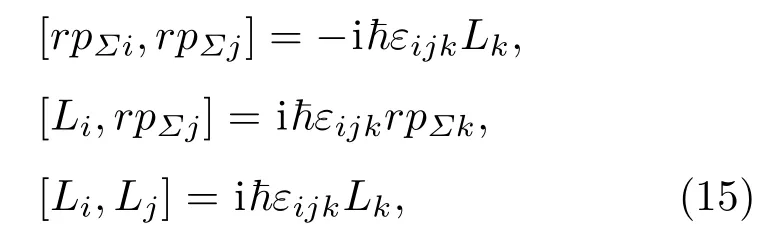
这样可以取一个力学量完备集为(r,Lz,rpΣz).算符rpz的本征值方程为

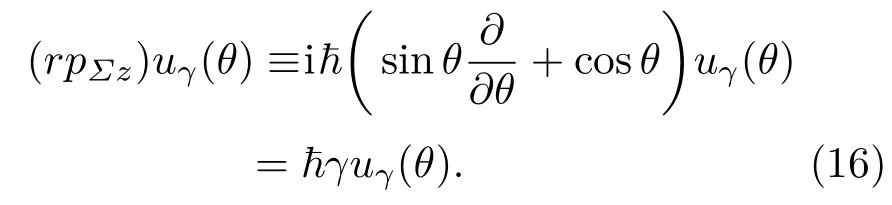
不难求得本征值为,γ∈(-∞,∞),相应的δ函数归一化本征函数为

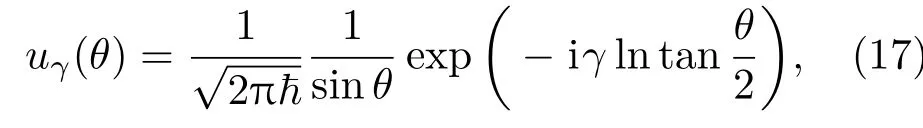
即可得三个力学量(r,Lz,rpΣz)同时取确定值的本征函数集合为

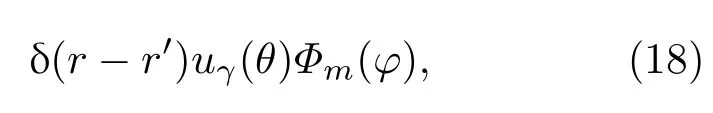
2.2 三维各向同性谐振子

三维各向同性谐振子的哈密顿为[21]

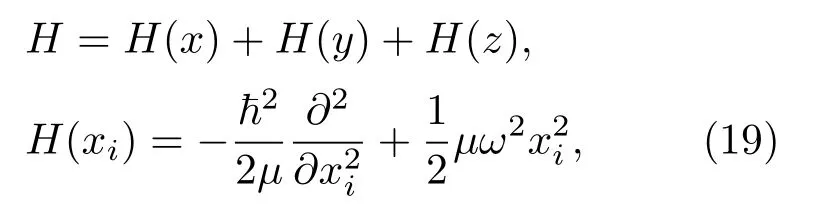
其中i=1,2,3,定态波函数可以选为三个对易力学量H(x),H(y),H(z)的共同本征函数,也就是

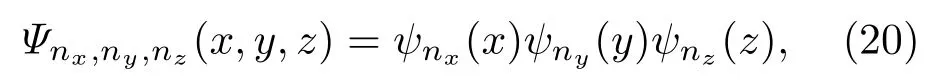
其中ni=0,1,2,···,

能量本征值为

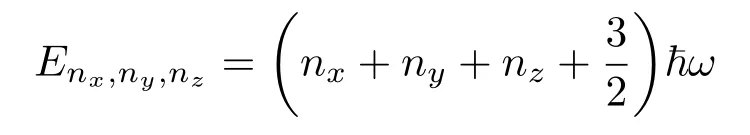
其中N=nx+ny+nz,第N个激发态具有(N+1)(N+2)/2重简并.

在球坐标下写出三维各向同性谐振子的哈密顿[21]

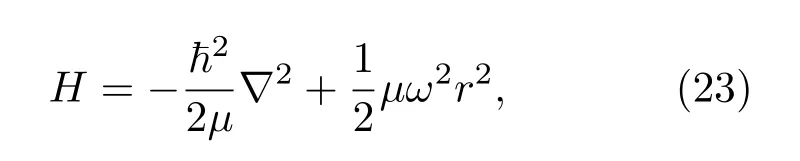
定态波函数可以选为三个对易力学量H,L2,Lz(符号取熟知的意义)的共同本征函数,也就是

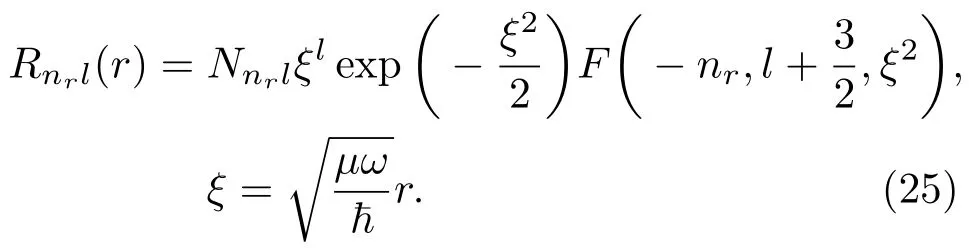
F(c1,c2,x)为合流超几何函数,归一化系数Nnrl的一般形式较为复杂,可以参考文献[18].能量本征值为

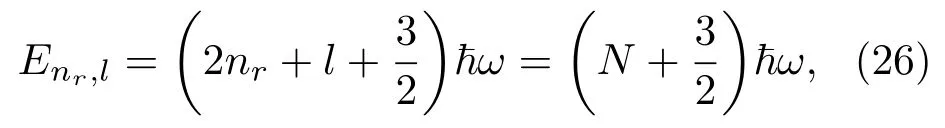
其中nr,l=0,1,2,3···,N=2nr+l,第N个激发态依然是(N+1)(N+2)/2重简并.

2.3 对态Ψnr,l,m(r,θ,φ)进行动量和几何动量分析的一般理论

相同能量本征值的两组基(20)和(25)之间相差一个幺正变换[21].本征态Ψnr,l,m(r,θ,φ)上给定N=2nr+l时,是直角坐标下的(N+1)(N+2)/2个状态的组合,即

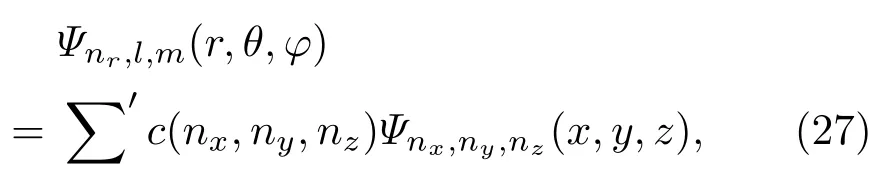
其中求和∑′表示对nx+ny+nz=N的所有可能求和,而且满足

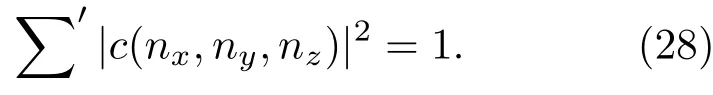
当N=0,c(0,0,0)=1.当N=1,c(nx,ny,nz)可以是一个矩阵,具体形式如下[21]

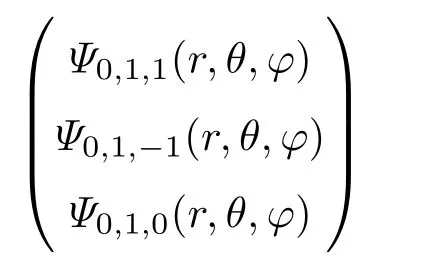
一般情况下,c(nx,ny,nz)是一个(N+1)(N+2)/2维的方阵,需要具体计算,这里不做展开.

下面给出在态Ψnr,l,m(r,θ,φ)上进行动量分析的一般方法.注意到对各向同性谐振子,考察空间一个方向就可以了,不妨选为z方向.对Ψnr,l,m(r,θ,φ)做如下展开:

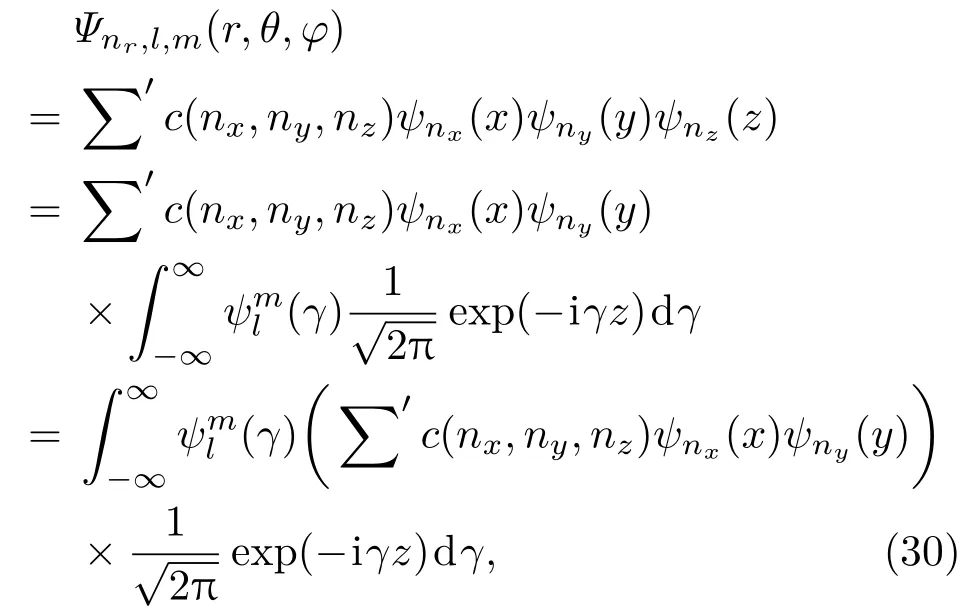
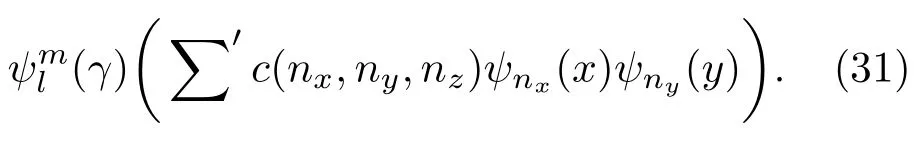
测量完成之后粒子动量取γ值的概率为

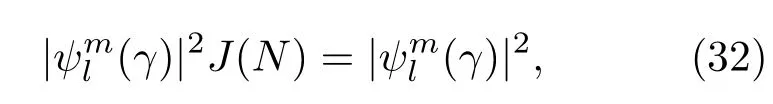
其中利用到了等式

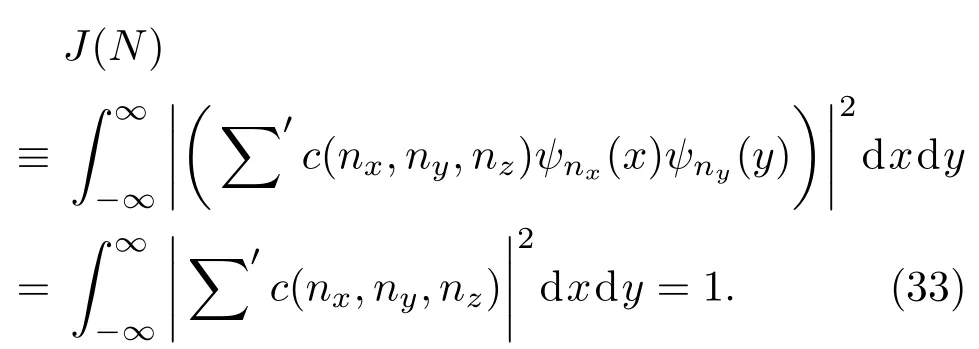
下面建立在态Ψnr,l,m(r,θ,φ)上进行几何动量分析的一般理论.

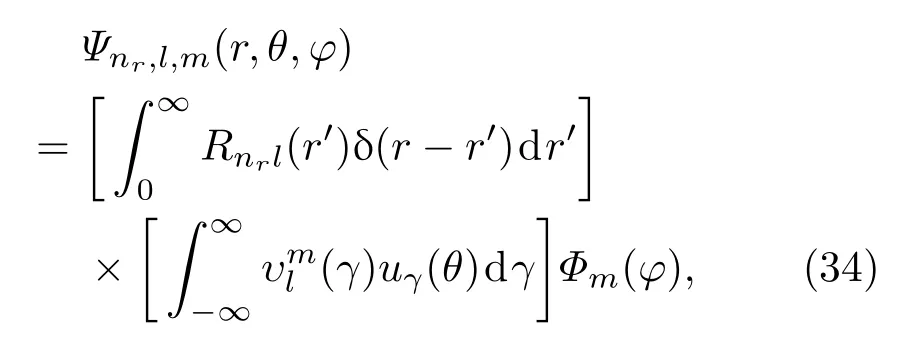
注意到于是问题的关键在于如何求得系数(γ),也就是对缔合Legendre函数进行几何动量z分量的本征函数进行展开,即

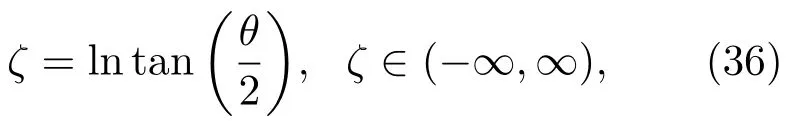
于是(35)式化为

也就是,(γ)是函数换.不难得到在l=0,1时展开系数(γ)的具体形式如下:的傅里叶变

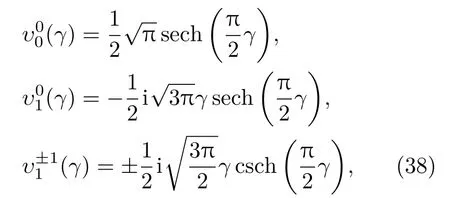
其他更多的υm l(γ)的具体形式可以参见文献[3].

2.4 在Ψnr,l,m(r,θ,φ)上对动量和几何动量的测量以及意义

2.3 小节中建立了在态Ψnr,l,m(r,θ,φ)上测量动量及几何动量的z分量的一般结果.给定动量和几何动量的某个确定间隔范围内γ→γ+dγ,概率分别为在实际测量这两个动量时,实验上直接记录是和这两个量的差,具有鲜明的物理意义.

注意到径向动量可以通过(8)式来定义,也就是可以通过如下方式来定义,

这样,如果测量pr的z分量,在实验上直接得到的结果是在其他分量上,也可以进行类似测量.

至此发现,即使(4)和(7)式中的径向动量本身由于不具有自伴性而不可以测量,经过等效定义就完全可以测量.不过这个测量是对两个力学量单独测量后的结果的差.

因此,对动量和几何动量的测量,可以实现对径向动量的测量.从而解决了径向动量本身由于不具有自伴性而不可以测量却存在不确定度的矛盾.这个矛盾较长时间是一个疑难[13-17].

3 三维各向同性谐振子的动量和几何动量分布的结果

下面利用第2节建立起来的一般理论,给出在一些态Ψnr,l,m(r,θ,φ)测量动量和几何动量的具体结果. 基态Ψ0,0,0(r,θ,φ)= ψ0(x)ψ0(y)ψ0(z)最简单.z方向的动量的分布是

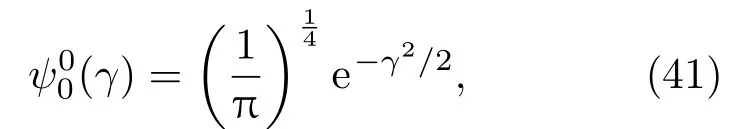
图1 基态上的几何动量(实线)和动量(点划线)z分量的概率分布,径向动量(虚线)z分量的测量值(靠近横轴)Fig.1.Probabilities of z-axis component of momentum(solid line)and geometric momentum(dashed line),and measurement values of radial momentum(dotted line),for ground state Ψ0,0,0(r,θ,φ).

第一激发态是一个三重简并的态,首先考虑态

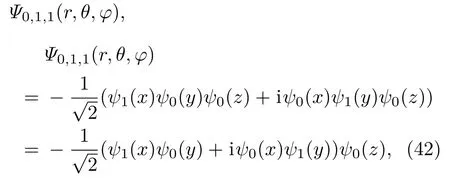
易知z方向的动量的分布是依然是(41)式,几何动量z方向的分布是(38)式中的(γ)=态Ψ0,1,1(r,θ,φ)上的几何动量(实线)和动量(点划线)z分量的概率分布,径向动量z分量的测量值如图2所示.

第一激发态中的第二个简并态是Ψ0,1,-1(r,θ,φ). 这个态上的几何动量和动量z分量的概率分布以及径向动量z分量的测量值也如图2所示.

第一激发态中的第三个简并态是Ψ0,1,0(r,θ,φ),

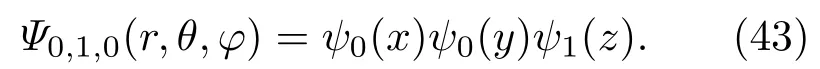
容易算符z方向的动量的分布是

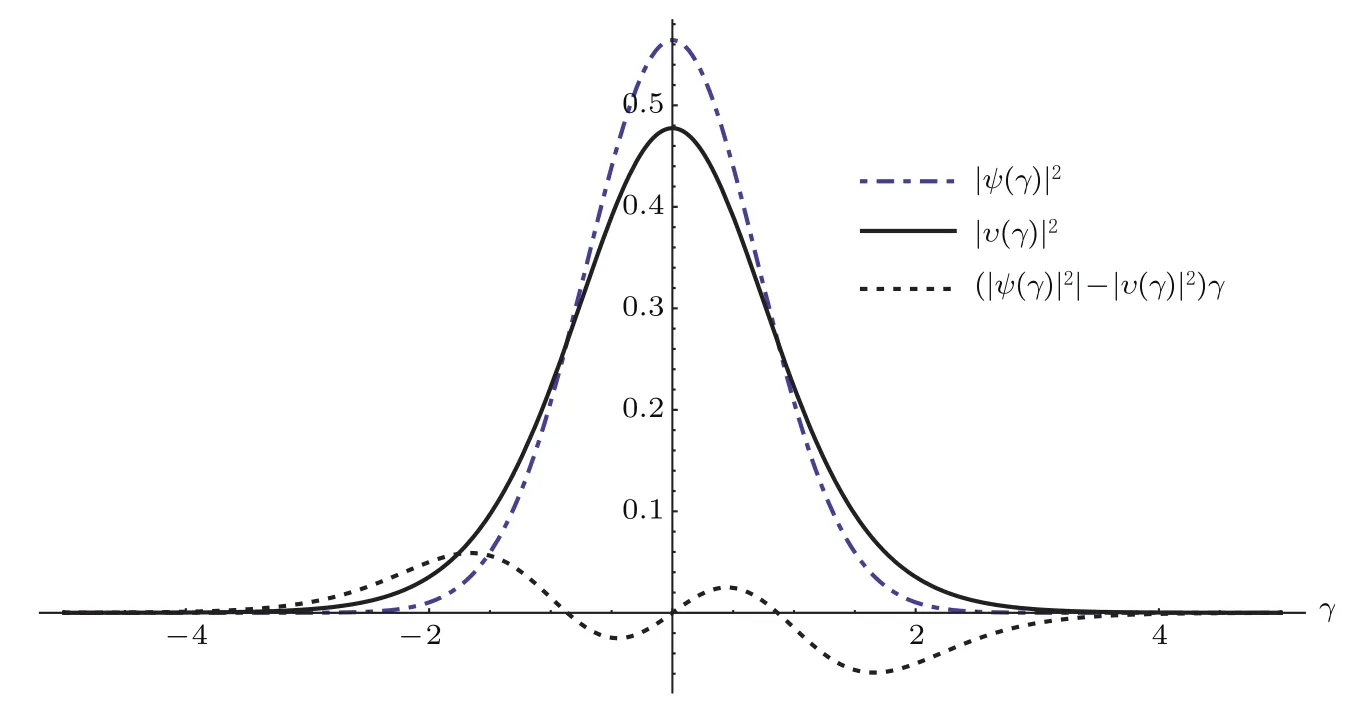
图2 态Ψ0,1,1(r,θ,φ)上的几何动量(实线)和动量(点划线)z分量的概率分布、径向动量(虚线)z分量的测量值Fig.2.Probabilities of z-axis component of momentum(solid line)and geometric momentum(dashed line),and measurement values of radial momentum(dotted line),for ground state Ψ0,1,1(r,θ,φ).

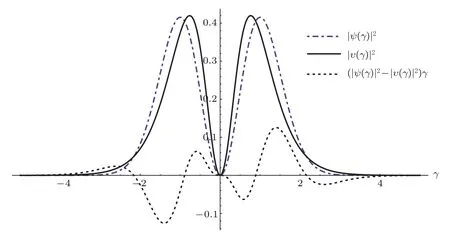
图3 态Ψ0,1,0(r,θ,φ)上的几何动量(实线)和动量(点划线)z分量的概率分布、径向动量(虚线)z分量的测量值Fig.3.Probabilities of z-axis component of momentum(solid line)and geometric momentum(dashed line),and measurement values of radial momentum(dotted line),for ground state Ψ0,1,0(r,θ,φ).

图1 至图3清楚地显示出,在一个确定的定态Ψnr,l,m(r,θ,φ)上,在空间的某个确定方向,动量分布和几何动量分布不但趋势完全一样,而且数值上也相差无几.由此可以合理地推测出,在这种定态下,在经典极限下,动量和几何动量其实是同一个概念.不需要复杂的计算,就可以直接理解这个结论.在定态Ψnr,l,m(r,θ,φ)上,如果量子数很大,径向位置将集中在一个较薄的球壳内,也就是粒子将在一个球面上运动.从几何动量的定义,就是粒子运动的动量.对于各向同性谐振子,在任何方向上,这个球面上的粒子,就是一个谐振运动,动量和几何动量都将出现同样的谐振运动特征[3].

图1至图3同时清楚地显示出,在一个确定的定态Ψnr,l,m(r,θ,φ)上,在空间的某个确定方向,动量分布和几何动量分布之间仍有差别.这个差别正好可以定义为径向动量在该方向上的分量.从量子测量理论的角度,径向动量是一个可观测量,而且径向动量的平均值为零.

4 结 论

最初引入几何动量的目的是为了给约束在超面上运动粒子的动量一个恰当的定义,后来发现可以用来描述粒子在全空间的运动在超面上的投影.很多曲线坐标系就由超面族和超面上的法向矢量作为一个坐标轴而构成,因此几何动量成为这些曲线坐标系下的一个力学量.在三维各向同性谐振子中,采用球坐标描述,存在球面族.由于超面上的几何动量必须投影到高一维的平直空间,而三维各向同性谐振子本身就在三维平直空间中进行描述,因此同时具有动量和几何动量分布.这两个动量的差,可以定义为径向动量,从而使得径向动量可以测量.通过各向同性谐振子基态、第一激发态上的具体计算发现,动量和几何动量的分布定性上近似,定量上相差不大.定量上的这个差别,就是径向动量的贡献.从而通过几何动量,可以显示出狄拉克引进的径向动量的物理意义.