基于遗传算法的3D动态实时建模方法

郑朝鑫, 董 晨, 叶 尹

(1.福州大学数学与计算机科学学院，福建 福州 350108； 2.福建省人大常委会，福建 福州 350001； 3.网络系统信息安全福建省高校重点实验室，福建 福州 350108)

0 引言

目前比较流行的3D建模方式是三维激光扫描点云建模方式，文献[1-2]展示了这种方式建模可以达到极高的模型精度.微软公司也推出Kinect，文献[3-4]介绍Kinect技术以及利用Kinect进行3D建模的实现方法.另外一种比较特殊的3D建模方式是从2D图片中进行抠图建模，文献[5]详细地介绍这种建模方法的具体实现以及技术细节.遗传算法(genetic algorithm，GA)是将生物界中的自然选择和种群遗传学原理引入到算法的搜索过程中，具有强大的鲁棒性以及搜索性能.文献[6]展示如何直接利用经典遗传算法来解决智能事件辨识问题、传感器数量配置优化问题.文献[7-9]研究遗传算法的改进方法以及具体的实现步骤，并用大量的仿真实验数据证明改进后的混合遗传算法具备更加强大的搜索性能.文献[10]提出一种基于遗传算法的入侵检测特征选择方法，提高系统的检测效率.文献[11]通过遗传算法中编码技术和基因技术分析，在社交网站数据分析过程中发现不良信息和违法信息.

1 3D建模

动态3D建模技术在家居装修中，将需要求解房间的长、宽、高, 以及用户身高作为多维空间中的一组可能解.利用遗传算法进行搜索计算最优可能解，最后得到8组标定向量误差最小的解.在本文中，需要利用陀螺仪传感器输出数据，实现测量立方体房间中心点与墙角连线的单位向量数值.这个过程中存在着设备误差以及人工站在房间中心点对准墙角位置进行辅助标定的人为操作误差，如图1.归纳可得本文中的优化问题是利用遗传算法对陀螺仪测量数据的各种误差进行有效性的优化，最后计算得到现场房间单位比例的长宽高尺寸.3D模型本身尺寸单位是点或者说像素，与现实物体尺寸只是比例映射关系，所以陀螺仪简易测量可通过遗传算法得到房间最佳的长宽高比例信息，即可实现3D建模目的.

图1 不同用户测量同一房间产生的坐标系原点偏差示意图Fig.1 Different users measure the frame origin deviation of the same room

2 遗传算法

2.1 编码方式

基因编码选择实数编码方式.系统需要求解的目标有4个实数值，分别对应房间长度、宽度、高度、用户身高，通过遗传算法将4个参数优化后，就可以通过3D引擎创建一个3D房间模型并设置正确的摄像头位置视野与实际房间尺寸及用户视野一一映射，如图2.

图2 各视野与实际房间尺寸一一映射Fig.2 Each view is mapped to the actual room size

算法种群第i个个体的编码定义为：Xi={w,l,h,b}，其中w为房间长度，l为房间宽度，h为房间高度，b为用户身高.在系统中用户操作进行标定的向量是8个，8个标定向量与个体信息间的关系如下式.

(1)

这样经过式(1)对解进行转换后，得到的8个向量就是遗传算法能处理的搜索空间，遗传算法可对这8个向量进行交叉、变异等操作，并与标定向量进行适应值匹配，如图3.

图3 房间墙角人工标定步骤示意图Fig.3 Schematic diagrams of manual calibration step in room corner

2.2 交叉操作

遗传算法的交叉方式描述如下： 第i个子代染色体的交叉概率Pc，如果满足执行交叉运算的条件，则双亲中的父亲就选择第i个子代染色体自身，数学表达为Xi={wi,li,hi,bi}，母亲染色体则通过随机选择方法获得，其数学表达式为Xj={wj,lj,hj,bj}，根据式(1)将父母的基因转换成两组8个向量的基因数据，在这个基础上进行交叉操作.

交叉操作具体步骤为： 1) 随机产生Pi∈U(0, 1), 当Pi>Pc，则这个染色体不满足交叉概率，不进行交叉运算，跳转到步骤8)，结束交叉操作; 2) 随机生成1～8的随机数，决定本次交叉的基因总数Ct; 3) 选择父亲染色体Xi，并根据式(1)计算得到父亲基因数据8个向量，随机生成1～8的随机数i，则选择第i个向量Vi作准备; 4) 随机选择母亲染色体Xj，并根据式(1)计算得到母亲基因数据8个向量，随机生成1～8的随机数j，则选择第j个向量Vj; 5) 随机生成步骤3)的随机数k，选择Vi的第k维分量浮点数，随机生成步骤3)的随机数m，选择Vj的第m维分量浮点数，将Vi的k与Vj的m进行交叉赋值实现向量Vi和Vj的交叉操作; 6) 交叉后的基因数据映射还原成新的染色体Xi和Xj替换原来的染色体数据，局部交叉成功; 7) 将Ct数值减1，判断Ct是否大于1，如果大于1，代表整体交叉操作尚未结束，跳转至步骤2)重复进行; 8)Ct为0，结束交叉操作.

2.3 变异操作

变异运算，采用染色体中的一个随机基因，用新的随机数赋值实现基因变异的目的.遗传算法变异方式描述如下： 子代第i个染色体Xi={wi,li,hi,bi}的变异概率Pm满足变异条件，则将染色体根据式(1)解码成基因信息得到8个向量数据，然后进行变异操作.

变异操作具体步骤为： 1) 随机产生Pi∈U(0, 1), 当Pi>Pm，则此染色体不满足变异条件，不进行变异操作运算，跳转至步骤6)，结束变异操作; 2) 选择变异染色体Xi，并根据式(1)计算得到8个向量的基因数据; 3) 随机产生ζk∈U(0, 1)，令j=(Int(ζk×8)+1) ，则j∈[1, 8]，这里Int表示取整运算.选择第j个向量Vj; 4) 随机生成一个符合向量取值范围内的浮点数更新替换向量Vj; 5) 变异后的基因数据映射还原成新的染色体Xi，更新染色体数据，完成第i个染色体的变异操作; 6) 结束变异操作.

2.4 选择策略

遗传算法通过选择操作模拟实现种群的繁衍过程.选择即是择优，因此选择操作是基于适应值计算结果的过滤方法，每个个体被选择的概率Pi计算公式如下：

(2)

种群进行选择操作具体步骤为： 1) 根据种群规模NP参数大小，设置择优操作的次数St=NP，初始化ids=0; 2) 准备对种群第ids个新染色体个体进行择优操作; 3) 随机生成一个0～1之间的随机数P; 4) 初始化i=0，从第i个个体Xi开始，根据式(2)计算Xi的选择概率Pi，令P=P-Pi.判断P是否大于0，如果P小于0，则跳转到步骤6); 5)i=i+1，跳转到步骤4)，继续进行轮盘旋转选择; 6) 得到种群中的第i个染色体，即选中染色体Xi.将Xi赋值给新一代种群中的第ids个空值染色体; 7) ids=ids+1，判断ids是否小于St，如果小于St，则跳转到步骤2); 8) 选择操作完成，新一代种群染色体赋值全部完成，结束操作.

2.5 解决房间尺寸计算问题

遗传算法首先设置一定数量的种群，种群中的每个个体对应问题的一个可能解.需要求解的参数数量N即为解的维度，算法具体实现过程描述为： 存在一个N维空间，其中有M个个体组成的种群.个体i的表达方式为Xi={X1,X2, …,XN}，采用随机赋值方式初始化种群，而后经过选择遗传、交叉、变异操作，迭代得到新一代的规模为M的种群.

将标定的8个向量Vi和可能解的8个向量Vxi都单位化之后，就具备在相同尺度下进行比较的条件，下一步骤为计算8对向量的向量差，并求向量差的长度值，最后求出适应值，计算公式如下：

(3)

(4)

式(4)是计算适应值的函数，其中DO的物理意义是可能解代表的房间墙角单位向量与实际房间墙角单位向量的偏差值.式(4)的前半段代表对8个DO偏差值进行累计，作为综合的偏差，偏差越大，数值就越小.偏差越小，数值就越接近1，即100%.后半段中，DO越小，代表两个单位向量偏差越小，可能解代表的墙角的空间位置与实际房间墙角位置越靠近，1-DO的值也就越接近1, DO越大，1-DO的值就越小.式(5)的计算结果代表可能解与现实房间相似度，理论最大值为1，代表可能解100%与现实房间匹配.

遗传算法实现具体步骤描述为： 1) 根据设计好的初始种群数量和遗传代数设定参数，并对种群中每个染色体数据结构用随机数进行初始化赋值，产生初始种群; 2) 执行循环体操作，对种群每个染色体Xi={wi,li,hi,bi}，根据式(1)计算得到8个向量，然后以8个向量为参数进行适值函数运算，适应值函数按照式(3)和式(4)计算可得.依此求得每个个体生存适应值fitness，并且保存记录具有最佳适应值的个体染色体信息; 3) 根据每个染色体个体的生存适应值执行选择策略，适应值越大则染色体被选择的概率Pi根据式(2)计算得到的数值越大，能获得的遗传生存几率越大，以此选择出下一代种群; 4) 对新一代的种群执行交叉运算操作; 5) 对新一代的种群执行变异运算操作.让种群的个体在选择、交叉及变异算子作用下不断向更好的适应能力方向进化; 6) 判定算法停止条件，如果循环次数达到预定的遗传代数NG，则退出循环操作，跳转至步骤7).如果不满足算法停止条件，则跳转至步骤2); 7) 所记录下来的最佳适应值就是最优解组合，可通过最佳染色体信息解算出房间的8个墙角顶点空间位置，结束算法.

3 改进遗传算法

由于遗传算法每次发生种群迭代时，主要的操作是择优，以保证新一代的种群比上一代更优，这是遗传算法的优势，同样也导致容易陷入局部最优.遗传算法设置跳出局部最优的操作是交叉和变异.在本文中，一种有目的性的尝试突破当前最优适应值的改进的择优操作方式被提出.有意识的突破最优的择优方式可参考粒子群算法的优化过程，当粒子群中有最优个体时，其他个体的迭代更新方式是有目的的优化.当遗传算法的种群择优就能提高种群的最佳适应值时，择优操作相比经典遗传算法得到改进.

3.1 实现步骤

改进遗传算法种群进行遗传时，大部分的步骤及其描述都是相同的，其中遗传操作的核心思想做了修改，从普通的择优遗传操作改进为有意识的突破最优的择优方式.具体步骤为： 1) 根据种群规模NP参数大小，设置择优操作的次数St=NP，初始化ids=0; 2) 准备对种群第ids个新染色体个体进行择优操作; 3) 随机生成一个0～1之间的随机数P; 4) 初始化i=0，从第i个个体Xi开始，根据式(2)计算Xi的选择概率Pi，令P=P-Pi.判断P是否大于0，如果P小于0，则跳转到步骤6); 5)i=i+1，跳转到步骤4)，继续进行轮盘选择; 6) 得到种群中的第i个染色体，即选中染色体Xi.利用粒子群算法中的公式对染色体的四维参数的所有方向进行预处理，计算所有方向的最佳适应值，有目的地留取最佳适应值数值最大的方向作为新染色体Xk, 令Xi=Xk; 7) 将有意识的尝试突破最优适应值的方式得到的新染色体赋值给新一代种群的第ids个空值染色体; 8) ids=ids+1，判断ids是否小于St，如果小于St，则跳转到步骤2); 9) 改进的择优操作完成，新一代种群染色体赋值全部完成，结束操作.

3.2 性能分析

对改进遗传算法和经典遗传算法的搜索结果进行横向对比.测试平台分别运行两种算法，令种群规模NP=800，交叉概率Pc=0.7，变异概率Pm=0.02，遗传代数NG=500.两种算法采用的参数完全相同，初始化时的目标解也标定为相同目标解，测试结果如表1所示.

表1 遗传算法及其改进算法性能实验

测试结果： 经典遗传算法得到的最佳适应值，不如改进的遗传算法.改进算法搜索得到的最优解比遗传算法更加逼近目标解.结果表明改进算法确实表现出更优的搜索性能.

从改进遗传算法的某个染色体角度比较.令种群规模NP=800，交叉概率Pc=0.7，变异概率Pm=0.02，遗传代数NG=500，目标解为{0.559 718, 0.204 419, 0.803 074, 0.209 286}，测试结果如表2所示.

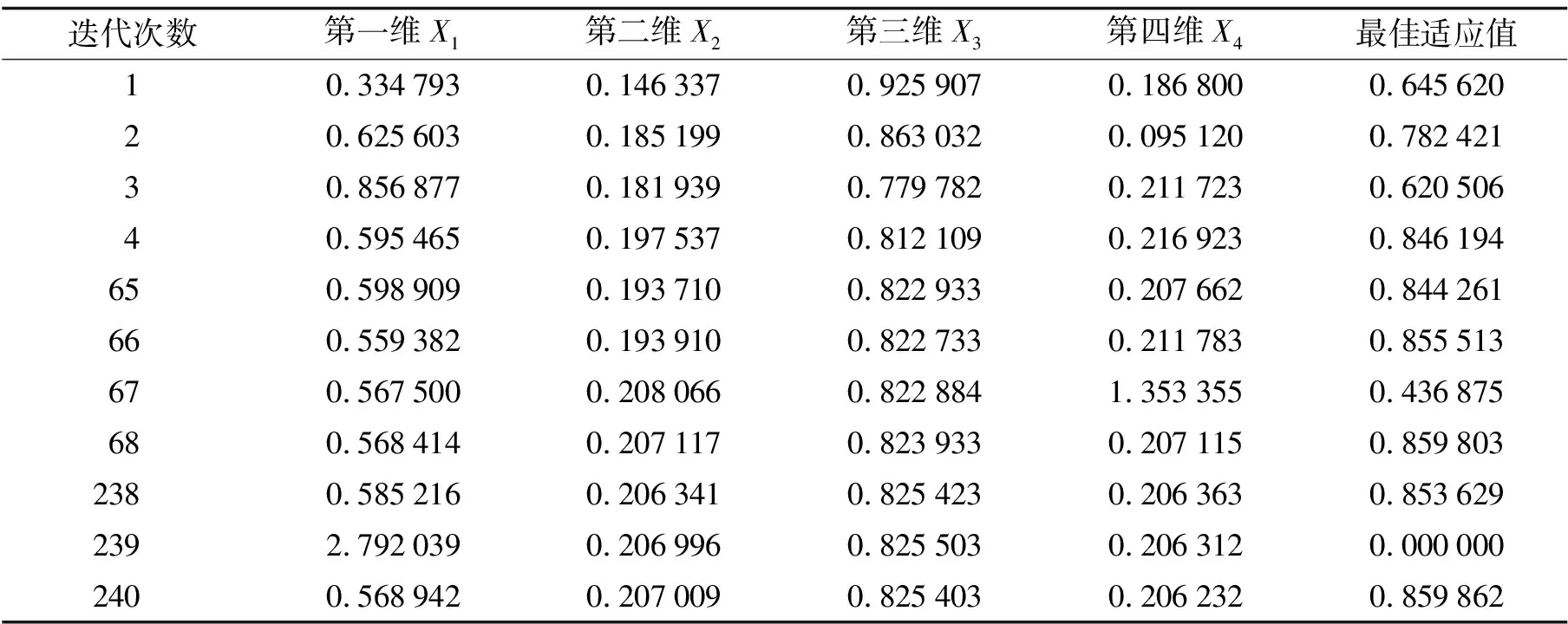
表2 改进遗传算法随机染色体个体迭代过程

从第一次和第二次迭代数据看出，改进遗传算法有强大的全局搜索能力，两次迭代后，个体快速向目标解靠近.第三次迭代中的第一维数据出现严重偏移目标解的现象，表明改进遗传算法的交叉或者变异机制触发了操作，这种操作也保证种群多样性.第四次迭代时，染色体更新信息来自适应值更高的上一代染色体.第67次迭代中的第四维信息、第239次迭代出现在第一维的信息，都是属于变异操作的影响.

4 实验结果与分析

使用遗传算法对6组不同长度、宽度、高度的房间以及不同身高的用户做动态3D建模优化实验，如表3所示.表中的偏差率代表计算出来的房间尺寸与现实房间尺寸的偏差大小，偏差率大小与算法计算出来的身高成正比.当算法随机产生的可能解中的身高越接近用户的真实身高时，算法计算得到的房间尺寸就无限接近真实房间尺寸.偏差率的大小不影响装修预览效果，预览匹配数值代表3D模型中对应的墙角空间位置与现实房间的墙角空间位置的匹配百分比.从实验数据知，预览匹配率平均在99%左右，说明该3D动态实时建模方法具有不错的精确匹配率.

表3 不同房间的遗传算法优化结果比较

5 结语

未来还可以研究提高改进遗传算法的运行效率方法，缩短算法运行消耗时间.可研究更好的适应值表达函数，使得适应值能更精确地表达虚拟房间与现实房间的相似度.目前只是针对立方体的房间进行测量并建模，在这个基础上以后还能对测量方法进行扩展，可增加支持不规则房间的形状及尺寸的测量建模，对室内窗口、门口、墙垛、梁等信息采集和处理，具有比较好的现实适应性，能在更多场合中使用，经过扩展的应用将有更好的发展前景.