探索国家开放大学数学与应用数学专业应用型人才培养研究——从微积分理论谈起

常会敏

（国家开放大学，北京 100039）

一、引言

微积分的产生可追溯到我国战国时期《庄子·天下篇》中曾提到的“一尺之棰，日取其半，万事不竭”；魏晋时期刘徽的割圆术思想——用圆的内接正n边形分割圆，当n的取值越大，正多边形的周长与圆的实际周长越接近，进而求得圆周率π的近似值。这其中蕴涵了分割、求和、极限等思想。除了文学、语言等文科性质专业外，微积分课程几乎是所有专业的必修课，微积分理论涉及领域的广泛性及重要性可见一斑。

国家开放大学（以下简称“国开”）坚持大众化教育，教育对象多是已经走向岗位的成年人。成人教育不同于全日制教育，具有显著的特点：1.学习时间有限。选择接受继续教育的成年人多是利用工作之余的时间学习，因而学习时间有限且理论基础相对薄弱。2.学习目的性强。选择成人教育多是为了提升学历、进修专业，因此他们会选择性的学习课本中认为最有用的知识，而不像全日制学生有时间和精力进行系统性的学习。3.学习形式多样化。除了普通的面授以外，他们最主要的学习方式是利用空余时间自学，网络学习等方式。因此，传统面授的教学设计和讲课思路对于成人教育不再适用，我们需要针对成人学习的特点，革新教学方法。

一般地，教材中介绍微积分的顺序是函数、极限、导数与微分、导数的应用、不定积分、定积分、积分的应用等。作为教师，这样链条式的讲给学生，逻辑上严谨，推理严密。然而，微积分定义较长且符号繁多，作为数学基础不扎实的学生很难理解概念并掌握，定义中一旦有一个符号不明白，就会对整个概念产生疑惑和不解。因此，我们急需打破传统课程构建模式，从解决实际问题出发，引起学生兴趣，使之掌握微积分知识的精髓，从而达到理解并会应用微积分知识解决实际问题的目的。

二、数学与应用数学现状及改革需求分析

（一）“大众化教育”背景下的数学发展

“大众化教育”相对于“精英化教育”，学生入学门槛低。作为一所“没有围墙”的大学，国开以宽进严出、面向全体社会成员为办学理念。在此“大众化教育”背景下，会出现学生入学时水平参差不齐、数学理论基础普遍较差的现象。然而，数学与应用数学专业作为一门基础理论性较强的专业，相关教材的内容设计和教师的讲课方式一直以来都是以严格的理论推导为主线，忽略数学知识的实用性，这与大众化教育背景下成人对于数学知识的需求是相悖的。因此，我们应以数学知识的应用性为主线，以培养学生应用数学知识解决实际问题的能力为目标，适当减少理论知识的推导和证明，化繁为简，产教融合。

（二）现有教材中关于微积分概念的引入没有体现成人教育的特点

纵观我国普通高校使用的微积分教材，导数和积分的应用都是放在章节末尾讲解。对于全日制学生来讲，他们有足够的时间去理解前面的理论知识，最后过渡到其应用顺理成章。而成人学习时间有限，且目的性强的特点使得他们在最开始学习时就迫切想知道为什么学习微积分理论，有什么用？因此，急需研究出版针对成人教育特点的微积分教材。

（三）教师忽略教学设计，学生理解概念困难

微积分知识中涉及了三个重要概念——导数、微分和积分。根据调查发现，学生普遍认为微分和积分的概念理解起来困难，导数和微分容易混淆等[1]。究其原因，还是学生没有充分理解微积分知识的内涵和应用。从教师的角度分析，照本宣科式的讲解，符号化的语言描述及严格的理论推导，冗长复杂的计算无疑会掣肘学生对微积分知识的理解。美国数学史家M.克莱因（Morries Kline）认为数学不应该是说得越严密越好，而要把它描绘成尽可能地靠直觉接受。作为教师，要有能建构数学概念的能力，即从生动形象的简单例子开始，让学生学会去猜想、构思，严格的理论推导只是最后的一步。

三、针对数学与应用数学专业发展的建议和措施

（一）教材内容的改革

1.介绍微积分理论产生的背景

人类认识微积分的过程并不是按照现有课本介绍的顺序发展的。微积分教材中应将微积分理论产生的背景作为介绍，放在教材最前面，使读者了解微积分概念的演变和发展，使之对微积分理论有一个直观感性的认识。

微积分理论是社会需求的产物。除了我国庄子和刘徽的割圆术蕴涵微积分萌芽，古希腊人阿基米德的著作《圆的测量》和《论球与圆柱》中提到拱形面积、球和螺旋线下的面积等曲线面积问题[2]，都为微积分的诞生打下基础。到了17世纪，由于生产力的发展和社会实践的需要，人们开始研究运动物体的变化率和复杂图形的面积问题。在前人工作的基础上，牛顿和莱布尼兹独立发表著作，从不同的角度阐述微积分理论。牛顿研究一个变量相对于另一变量的瞬时变化率，发表《流数法》、《分析学》和《曲线求积术》，以无穷小量为基础建立微积分。莱布尼兹则研究曲线的切线和极值，首次引入微分记号dx，发表《一种求极大值和极小值以及求切线的新方法》，从而创立微积分。然而牛顿和莱布尼兹都不能够将自己建立的微积分理论严格定义，从而引发了第二次数学危机以及芝诺悖论。为了解决危机及出现的矛盾，在实数稠密性理论完善的基础上，柯西利用ε-δ语言严格定义了无穷小量的概念，在函数上定义了极限和连续性的概念，在极限的基础上，重新定义和阐述微积分理论。经过数学家们的不懈努力，形成了现有的微积分理论框架。

2.重新安排教材章节内容，重视微积分知识的实用性

教材内容决定了课程之纲，合适的教材编排能够帮助学生理解概念。

①积分相对于微分学比较容易理解，且按照微积分历史发生的顺序，积分学早于微分学，故可将积分学放在微分学的前面讲述。

③对于微分学篇，首先，在简单理解导数意义的基础上，介绍导数的计算。包括导数的四则运算、常见导数的基本公式和复合函数求导等。其次，着重讲解导数的应用，即通过生活中的实例介绍导数的应用领域。例如，导数在几何学中可以用于求曲线的切线、斜率、极值和最值等问题；在物理学中可以用于求运动物体的瞬时速率和变力做功等问题；在经济学中可以用于求需求弹性、边际利润及收入最大化等问题。通过具体的应用介绍，使学生产生强烈的求知欲，暂时绕开理论知识的推导，更容易使学生形成形象直观的感受。微分以导数为工具，用于求函数改变量的近似计算。导数和微分无论从定义还是从应用来说，都是两个完全不同的概念，学生之所以容易混淆二者，是因为定义复杂记不住，求微分时也需要求导数，感觉二者没有区别，却没有从应用的角度将二者彻底区分开。最后，将极限、导数和微分的严格定义作为升级内容留给感兴趣的同学进一步了解。这样的章节设计，既满足了基础理论较差学生的需求，又不妨碍高层次学生对理论知识的渴求。

（二）教师应注重教学设计，不断提高教学水平和教学质量

教师就是教材的“代言人”，是连接学生需求与教材之间的桥梁。根据学生的学习特点，精心的教学设计会带给学生事半功倍的学习效果。就微积分理论而言，可从不同的角度设计教学过程，在学生的思维水平范围之内，使之掌握知识并能够解决实际问题。

1.利用发生教学法，激发学生的学习兴趣

发生教学法是托普利茨（O.Toeplitz）早在1926年提出的一种教学思想方法，即依据历史发生原理，教师根据需要重构历史，追溯问题的本源，以便找到所要解决数学问题的核心所在[4，5]。

学生在学习一个新知识点的时候最想知道的是来源于哪里？所要解决什么样的数学问题[6]？通过发生教学法，教师可以介绍微积分产生的背景，重点强调积分最早用来求封闭图形的面积（如阿基米德与抛物线），导数用来求瞬时速率、切线斜率等，微分则用于求函数微小变化量的近似值。

其次，教师可通过介绍第二次数学危机和芝诺悖论的典型例子，使学生充分理解极限的概念，激发其求知欲。例如下面的例子：

例2：0.999999999……（无限循环下去）与1是否相等？

通过以上两个问题，引发学生的讨论，以达到发生教学法的目的。

2.利用微电影和几何图形等教学工具，加深学生的理解能力

数学专业不同于其他学科，理论知识较强，公式符号繁杂，难以引起学生的学习兴趣，容易使学生产生倦怠。利用网络工具，教师可通过制作微电影方式[7]，使学生参与视频制作，从而提高学生观看的积极性，同时将微积分知识形象的展示在学生面前，例如国开的5分钟课程，通过时间短、内容精的微课，学生使用平板、手机等移动设备，利用碎片化的时间即可方便的学习。教师亦可利用漫画形象、寓教于乐的特点，通过制作动漫的方式，将微积分知识通俗易懂的展现给学生。

图1 导数的概念

3.通过实例分析，培养学生解决问题的能力

微积分知识应用领域广泛，教师可通过实例讲解，启发学生思考，以培养学生利用数学知识解决实际问题的能力。

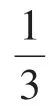
在近似计算中往往用到微分知识。例如：一个半径为10cm的金属圆片，受热后半径伸长了0.05cm，问面积增大了大约多少？设面积S=πr2，则ΔS≈ dS=S'Δr=2πr.Δr= π，因而可求出面积大约增长了π。

四、结束语

根据“社会需求，因材施教”的原则，深化产教融合，如何培养社会需求的应用型数学人才，是值得深入思考的问题[8]。从教材改革出发，注重数学知识的应用性，弱化理论推导；结合社会热点，列举与数学有关的热门问题，培养学生应用数学知识解决实际问题的能力。教师应注重教学设计，利用网络资源，多将实用且有趣的例子应用于教学课堂，将抽象的概念形象具体化，提升学生学习兴趣的同时，使知识点易于接受和理解。统筹兼顾，多策并举，以期为社会培养具有实践能力和创新精神的应用型数学人才。