差分像运动视宁度优化监测法*

王子跃， 任德清

(1.中国科学院国家天文台南京天文光学技术研究所，江苏南京 210042；2.美国加州州立大学北岭分校，物理与天文学系，美国加州北岭 91330-8268；3.中国科学院大学，北京 100049)

弗洛伊德参数r0即大气光学相干长度，是衡量一个台址大气视宁度的重要参数。运用差分像运动法通过测量星像相对位置的变化计算r0值，能够有效地消除非大气因素对大气视宁度测量的影响，使得测量结果更加准确可靠。差分像运动视宁度监测仪是以此原理设计研制的。

现如今，在量化天文视宁度领域，最普遍的方法是差分像运动测量法，由Sarazin和Roddier两位科学家在1990年为欧洲南方天文台选址时提出[1]。它由一个35 cm口径的望远镜和一块有两个子瞳的掩模组成，最后连接一块CCD。对于经过地球大气的单一目标光源，差分像运动视宁度监测仪测量其在望远镜入瞳面的两个子瞳上的波前到达角的相对方差，求得大气视宁度参数r0。该方法的优点是能有效消除望远镜由于风力载荷造成的追踪星轨误差、仪器抖动等非大气因素的影响，具有足够的时空精度，便于野外选址使用。1980年以后，很多优良台址和新的选址工作都使用了差分像运动视宁度监测仪，例如：西班牙LaPalma天文台选址[2]，日本Subaru八米望远镜选址[3]，国内有云南天文台丽江高美古2.4 m望远镜选址[4]等。然而，差分像运动视宁度监测仪在测量过程中入瞳掩模的尺寸是固定的，所以一次曝光捕捉的图像上只能得到一组固定子瞳间距的星像相对位移信息。

DIMM方法只能够测量总的大气视宁度，无法对某一层高度的大气视宁度进行测量，而三维大气视宁度测量是设计多层共轭自适应光学系统的前提，针对该问题文[5]于2015年提出了多子孔径日间视宁度监测仪(Multiple-Aperture Seeing Profiler，MASP)[5]，用来测量日间大气视宁度。它由两个口径40 cm的望远镜组成，选取双星作为导星，在0～30 km范围分多层对大气湍流进行分析，进而得出大气视宁度参数r0。它可以将大气湍流测量高度提升至30 km，等同于112 cm大口径望远镜所能测量的高度。多子孔径日间视宁度监测仪具有成本低、可移动性强等优点，尤其适合还不具有大口径望远镜的新台址。但是一般情况下，只需测量总的大气相干长度r0，无需对多层大气湍流进行量化，另外多子孔径日间视宁度监测仪用到两台望远镜使得架设过程较为复杂，不便于总体大气视宁度的测量工作。

本文提出一种名为差分像运动视宁度优化监测法：I-DIMM。该方法在差分像运动视宁度监测仪[1]的基础上进行改良，不再采用瞳孔掩模制造子瞳的方式，而是改为在望远镜瞳面上选择两个间距20 cm的子孔径，通过应用多子孔径日间视宁度监测仪计算大气视宁度参数r0的方法，对两个子孔径采集到的星像像差法处理，使得计算得到的r0值更为精确。此外，相较于DIMM法，I-DIMM系统通过改变两个子孔径之间的距离，得到不同子孔径间距情况下的r0结果，尤其在较小子孔径间距(1.6～3.0个子孔径直径距离)时，I-DIMM计算得到的r0值比DIMM法更精确。

1 I-DIMM系统描述

应用于欧洲南方天文台选址的差分像运动视宁度监测仪光学结构[1]如图1，传统的DIMM系统通常在小口径(比如180～350 mm)望远镜的入瞳处放置一块有两个子瞳(50～100 mm)的掩模，并在其中一个子瞳上放置光楔，使到达这个子瞳的波前产生倾斜，从而同一目标星经过两子瞳后产生不重叠的双像，最后用探测器记录下一系列双像的瞬时状态，并统计双像相对位置的方差，即可计算出视宁度。本文用于对比的传统DIMM系统即为此结构及原理。具体参数见表1。

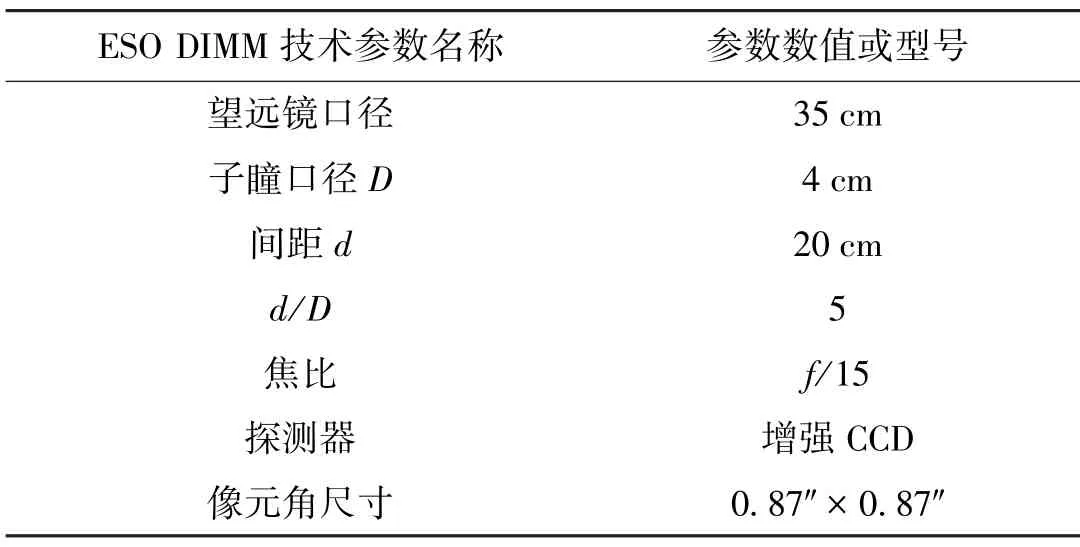
表1 欧洲南方天文台DIMM参数Table 1 ESO DIMM Parameters

图1 差分像运动视宁度监测仪光学系统示意图Fig.1 DIMM Optical Scheme

本文的I-DIMM系统在模拟时采用微透镜阵列将望远镜瞳面分割成多个子孔径，如图2。将有效的哈特曼子孔径的线性阵列进行编号，如图3。

图2 I-DIMM工作流程图Fig.2 I-DIMM workflow diagram

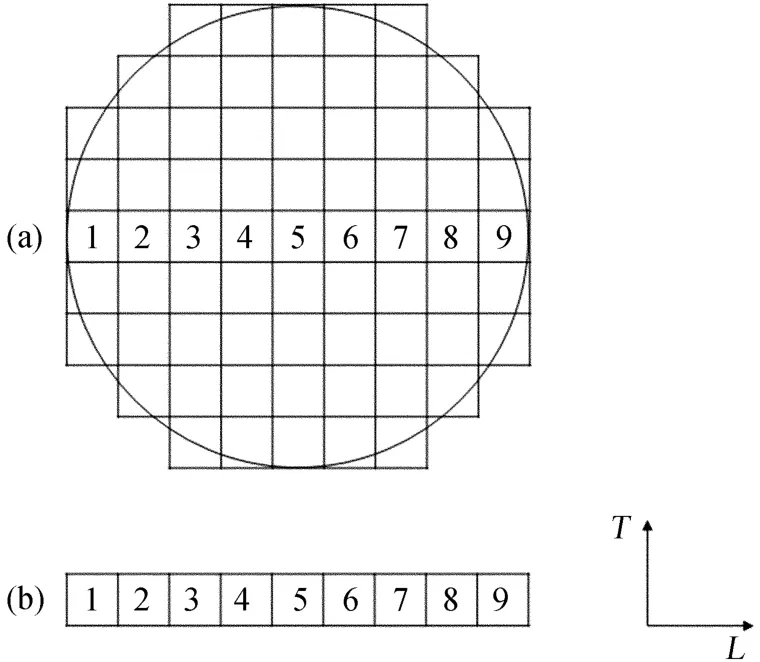
图3 I-DIMM夏克-哈特曼波前传感微透镜阵列Fig.3 I-DIMM SHWFS lens let array

如图3的I-DIMM系统中，在直径长度上由9个哈特曼子孔径组成，相当于将望远镜瞳面直径方向上等分为9个子孔径(如图数字1～9)，每个子孔径的直径4 cm，与DIMM中子瞳口径相等(参见表1，欧洲南方天文台DIMM参数表)。在同一行的哈特曼子孔径阵列中，相邻两个数字代表的孔径相距为一个子孔径直径的距离，即1D。以此类推，数字间相差为2的两个子孔径间距为2D，当数字间相差为5时，两个子孔径间距5D，相当于DIMM中两个子瞳相距20 cm。这样在结构模型上完成了I-DIMM系统与DIMM系统的一致与统一。对于一个固定的子孔径间距，每一行阵列可以至少提供一种子孔径的组合方式。以图3(b)为例，子孔径1与2的组合间距为1D，而子孔径3与4的组合间距也为1D，以此类推，间距为1D可以找到8种子孔径组合。图4展示了直径不同的夏克-哈特曼子孔径组合的数量与对应的孔径间距之间的关系。

图4 夏克-哈特曼子孔径组合数量与孔径间距的关系Fig.4 Number of sub-aperture pairs versus the sub-aperture distance

2 I-DIMM计算理论

传统的DIMM法[1]中，在L方向(沿着子瞳中心连线方向)差分像位移方差的表达式为

T方向(垂直于子瞳中心连线方向)差分像位移方差的表达式为

两者方差可以用单个孔径的二维运动总方差σ2表示：

理论上，假设S＝d/D，应用(3)式应满足条件：S≥2。(1)、(2)式简化为

其中

针对性训练1：一条多肽链的分子式为C22H34O13N6，其彻底水解后，只得到下列下列3种氨基酸：谷氨酸（C5H9O4N），甘氨酸（C2H5O2N），丙氨酸（C3H7O2N）。则该多肽链彻底水解可产生多少个丙氨酸？ （ ）

文[1]给出的上述近似表达式已经对文[6]的表达式进行了改进，在d＞D/2时能够和文[6]给出的近似值良好匹配[1]。例如，当S＝1时，沿着子瞳中心连线方向的差分像运动位移方差近似值偏差率为-0.2%，但是在垂直于子瞳中心连线的方向上，差分像运动位移方差却偏差了-17.3%；当S＝2时，垂直于子瞳中心连线方向的差分像运动位移方差依然偏差较大，有-9.0%之多。所以，为得到更精确的r0估计，本文将S趋近于0的情况也考虑其中，引用文[5]在多子孔径日间视宁度监测仪中的近似表达式：

其中：

由于本文研究导星数量为1，且仅评估总的r0值，故θ＝0，hn是望远镜垂直上空大气湍流的叠加。再联合S＝d/D，(10)式、(11)式改写为

对于方形子孔径，文[7]指出，函数II-DIMM(i，0)和函数的定义分别为

引入函数 Comp(II-DIMM/IDIMM)：当 II-DIMM/IDIMM＜1时，函数值为0，即 II-DIMM＜IDIMM，否则为 1，即II-DIMM＞IDIMM。表2和表3给出了在两个方向上，Fried近似值、IDIMM和II-DIMM3种r0计算方法在不同孔径分离比下的二维运动关系偏差值。

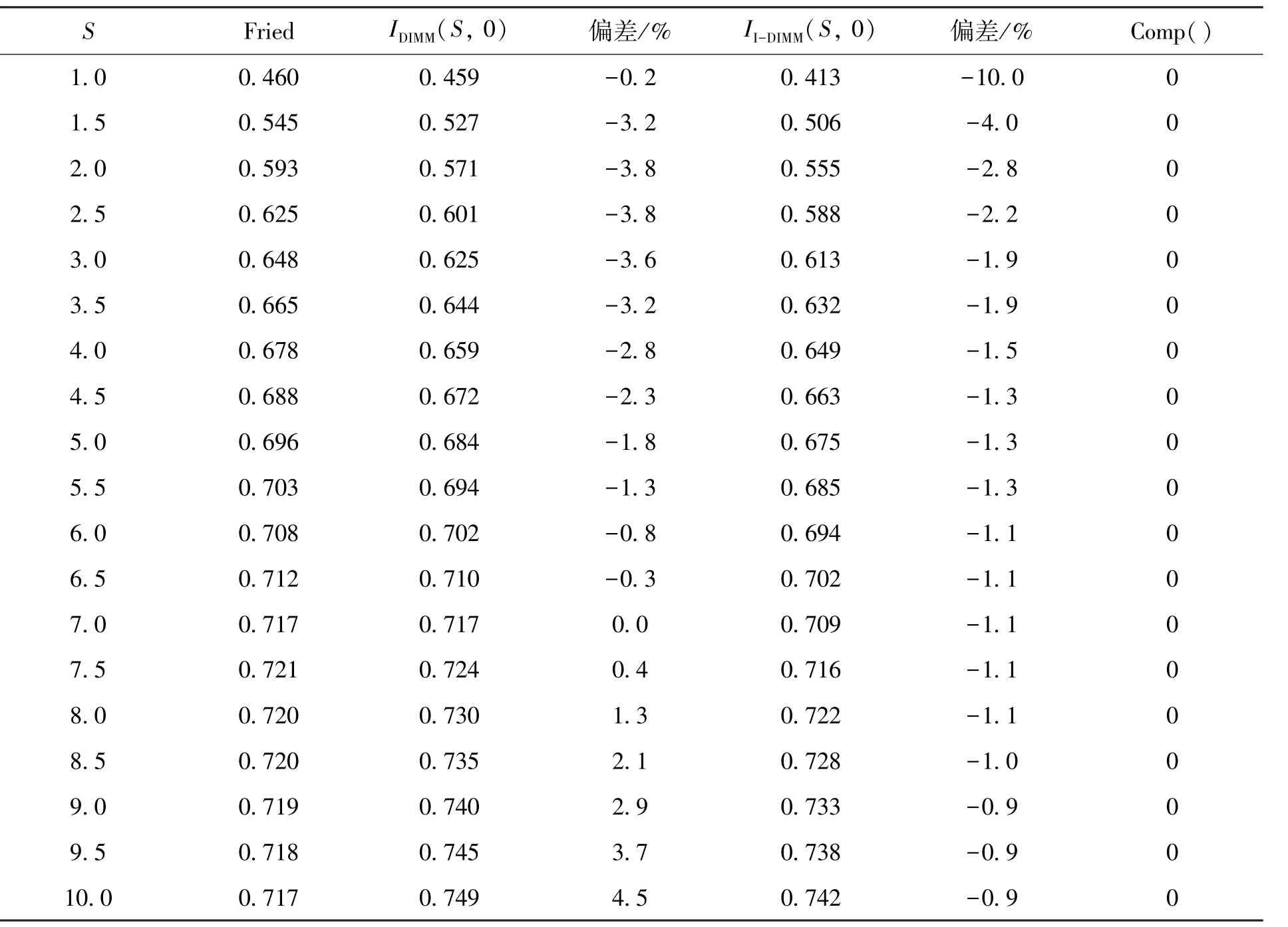
表2 L方向3种方法在不同孔径分离比下的二维运动关系偏差Table 2 Difference of two-dimensional motion for various aperture-to-separation ratios in longitude by three methods

表3 T方向3种方法在不同孔径分离比下的二维运动关系偏差Table 3 Differences of two-dimensional motion for various aperture-to-separation ratios in transverse by three methods

其中，IDIMM的偏差值是与Fried给出的近似值比较的结果，II-DIMM的偏差值是与IDIMM值比较的结果。

图5和图6给出了两个方向上3种方法在不同孔径分离比的二维运动关系曲线。

图5 3种方法中L方向不同孔径分离比的二维运动关系曲线Fig.5 Graphs of two-dimensional motion for various apertureto-separation ratios in longitude by three methods

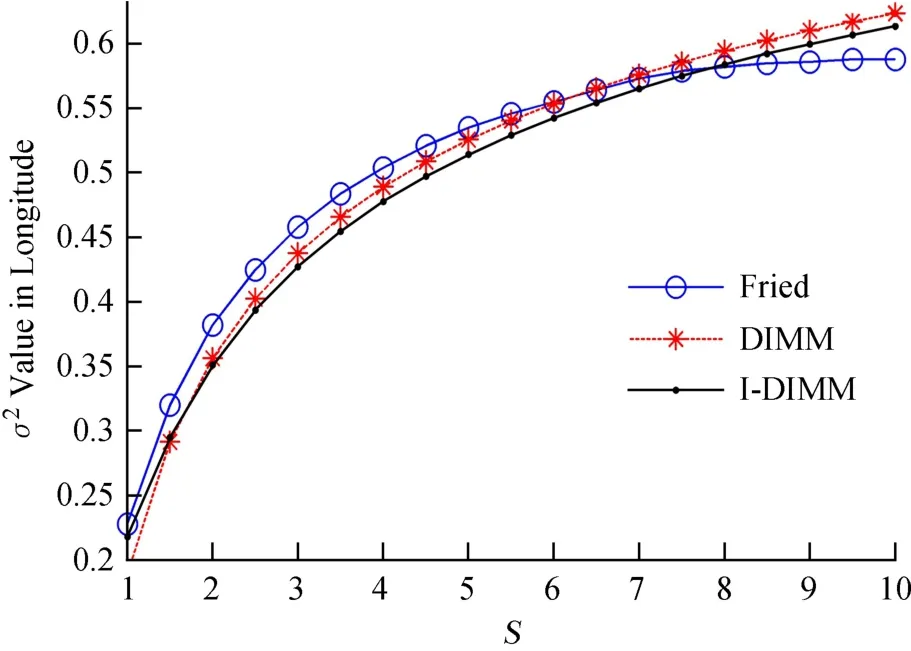
图6 3种方法中T方向不同孔径分离比的二维运动关系曲线Fig.6 Graphs of two-dimensional motion for various apertureto-separation ratios in transverse by three methods

图5和图6直观地显示，改进后的II-DIMM在L方向上均小于IDIMM。T方向上，当S＜1.6时，II-DIMM略大于IDIMM；当S≥1.6时，II-DIMM均小于IDIMM。尽管IDIMM是文[1]针对欧洲南方天文台DIMM圆形子孔径的简化公式，而II-DIMM是针对线性类方孔径的简化公式，但根据表2和表3的量化比较，在S≥1.5时，两种简化表达式相差仅仅在2%上下，孔径形状的不同不会对计算结果带来明显的误差。

3 I-DIMM与DIMM对比模拟

3.1 子孔径间距20 cm时I-DIMM与DIMM对比模拟

本文使用专业光学软件YAO(Yorick Adaptive Optics，YAO是被广泛公认的用以模拟不同大气及星源条件下点扩散函数成像的软件)。在Linux环境下运行YAO，设置望远镜口径为36 cm，直径方向上设置9个子孔径，每个子孔径直径4 cm，设置与传统DIMM相同的望远镜参数[1]，这样，I-DIMM在硬件上与DIMM完全相同，所以排除了两种方法在计算r0值时因为硬件原因导致的差异与误差，最终结果的差异完全因为计算公式的差异。在硬件上通过设置大气湍流参数，初始化r0，设置值0.1 m(std＝0.1)，运行仿真软件得到一系列光源的点扩散函数模拟图像，仿真DIMM中差分像运动图像的曝光捕捉。具体设置参数如表4。

每次模拟处理2 000幅点扩散函数图像，共模拟100次。利用图像质心算法求得每一个子孔径上图像质心在L(沿着子瞳中心连线)和T(垂直于子瞳中心连线)方向的坐标，结合差分像运动算法，求得在两个方向上的大气视宁度参数r0值，图7和图8分别给出了L和T两个方向上，S＝5时，100次模拟求得的r0值。

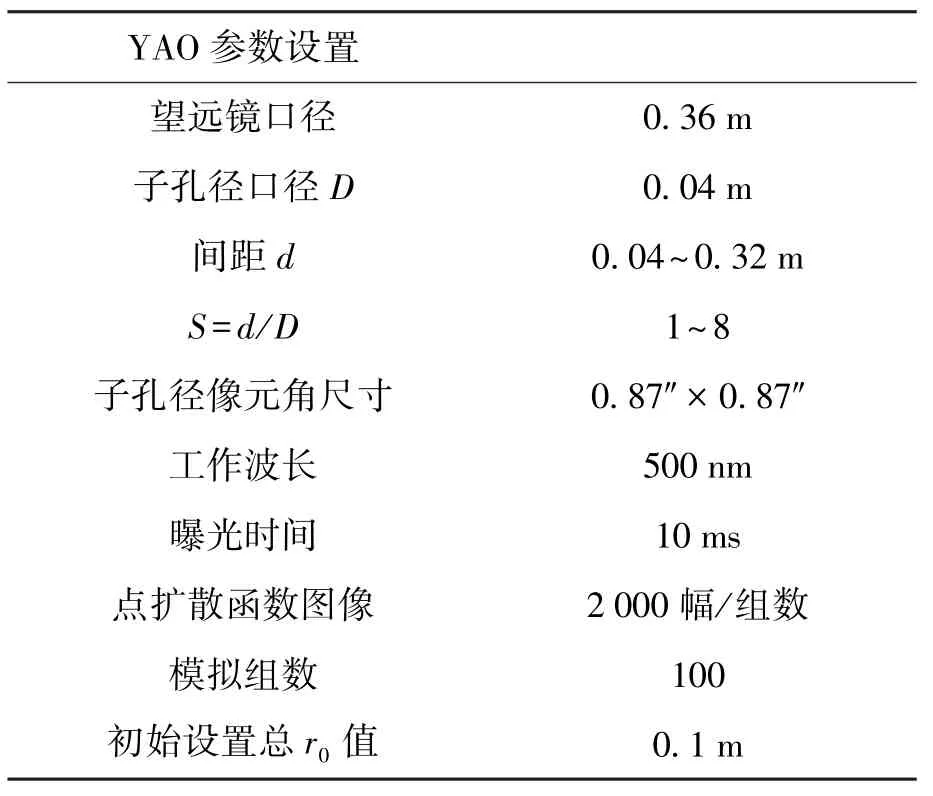
表4 YAO参数设置Table 4 Software YAO setup parameters

图7 S＝5时L方向100次模拟r0计算值Fig.7 S＝5 results of r0 by 100 times simulating in Longitude

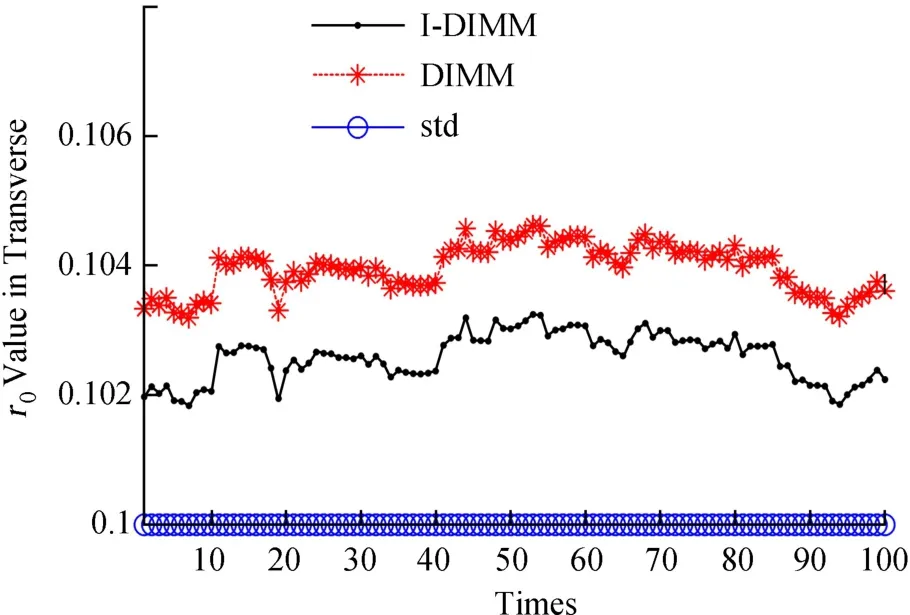
图8 S＝5时T方向100次模拟r0计算值Fig.8 S＝5 results of r0 by 100 times simulating in Tranverse

如图7和图8，当子孔径间距20 cm，即孔径分离比S＝5时，100次模拟中I-DIMM测量r0值均比DIMM更接近设置值0.1 m。L方向上，I-DIMM测量r0平均值为0.100 8 m，误差0.8%，小于DIMM的误差1.6%；T方向上，I-DIMM测量r0为0.102 6 m，误差2.6%，小于DIMM的误差4.0%。图9给出了100次模拟总r0计算值。

I-DIMM测量总的r0平均值为0.101 7 m，误差1.7%，小于DIMM的误差2.8%。所以证明了IDIMM得到的r0值比传统DIMM法得到的更加精确。

3.2 方形子孔径误差模拟

本文3.1节证明了改用I-DIMM计算公式，可以提高r0计算值的计算精度，但是，传统DIMM采用的公式是在1990年提出的，由于当时计算能力有限，再加上主要应用于圆形子孔径，与本文模拟时的方形孔径有差别，必然导致一定的计算偏差。尽管在第2部分论证了与I-DIMM公式误差仅仅在2%左右，完全可以忽略。但是，为了排除DIMM针对圆形子孔径计算公式带来的误差，进一步验证运用I-DIMM对计算精度的影响，对两种方法中的r0计算均采用I-DIMM的计算公式。不同的是，模拟孔径间距为20 cm的传统DIMM计算时只处理孔径1和6的像差分信息，而在模拟I-DIMM时，如图4，I-DIMM系统的微透镜阵列在直径方向上最多可以提供4组孔径间距为20 cm的像差分信息，所以为计算r0值提供了更多组数。以一次模拟2 000幅点扩散函数图像计算r0为例，I-DIMM相当于处理8 000幅点扩散函数图像，是DIMM处理像差分信息量的4倍。表5给出了对20次模拟，每次模拟2000幅图像得到总r0平均值的结果。

如表5，I-DIMM计算总r0平均值为0.101 7，误差为1.7%，比只处理一组信息的DIMM法计算误差1.9%更加精确，所以，在处理相同数量图像时，I-DIMM计算更多的子孔径像偏移信息，计算值也比DIMM更精确。

3.3 子孔径间距比S≤3时I-DIMM与DIMM对比模拟

根据文[1]的理论，使用DIMM时要求S≥2，而实际的望远镜未必一定满足这一条件，比如，美国国家光学天文台和欧洲南方天文台的选址[3]，也刚刚达到S＝2，再比如，台湾鹿林天文台的选址[3]，S＝1.6。实际上，当S越小(S≤3)，望远镜口径也能随之越小，更便于选址作业。为了评估S较小情况下I-DIMM测量r0值的精确程度，本文详细分析了S较小(S≤3)时的情况。图10与图11分别给出了S较小时100次模拟r0计算平均值。

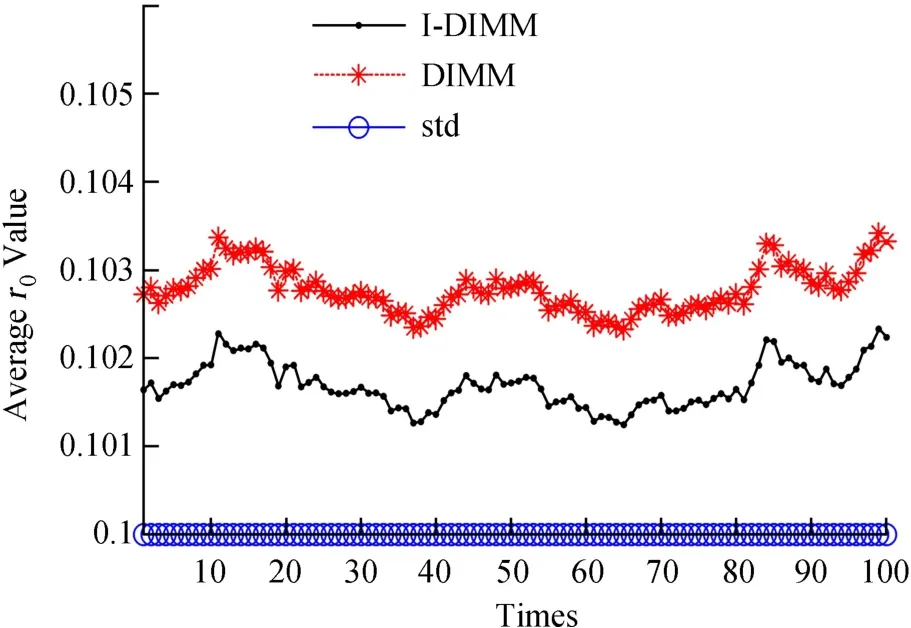
图9 S＝5时100次模拟总r0计算值Fig.9 S＝5 results of total r0 by 100 times simulating

表5 总r0平均值Table 5 The average results of total r 0

图10 0.36 m望远镜L方向r0计算结果Fig.10 Results of r0 in longitude via 0.36m telescope

图11 0.36 m望远镜T方向r0计算结果Fig.11 Results of r0 in transverse via 0.36m telescope

如图10，在L方向上，I-DIMM法求得的r0值均小于DIMM法所求值，且距离r0设置值的基准线更近，说明I-DIMM法求得的r0值更精确。实际数值上，当S＝1，2，3时，I-DIMM计算r0值分别为0.116 4 m，0.103 1 m和0.100 7 m，误差分别为16.4%，3.1%和0.7%，均小于DIMM计算r0值误差24.1%，4.9%和1.9%。在T方向上，当S＝2，3时，I-DIMM法计算r0值为0.104 6 m和0.101 9 m，误差4.6%和1.9%，均小于DIMM法误差5.6%和3.5%，且I-DIMM曲线距离r0设置值的基准线更近，证明了I-DIMM法计算r0值在T方向同样更为精确。由于r0与I(I-DIMM，DIMM)的单调性一致，当II-DIMM大于IDIMM时，I-DIMM的r0计算值也大于DIMM，如图6，当S＜1.6时，II-DIMM＞IDIMM，所以当S＝1时，I-DIMM法计算值大于DIMM法所求的r0值，偏离基准线也更远。图12给出的100次模拟总r0值的平均值，同样印证了上述结论。

4 0.12 m口径望远镜I-DIMM的模拟

在软件YAO上，设置望远镜口径为12 cm，子孔径直径4 cm，子孔径间距8 cm，即S＝2，初始r0设置值0.03 m(std＝0.03)，具体参数如表6。

图12 0.36 m望远镜总r0计算结果Fig.12 Results of Total r0 via 0.36m telescope

表6 YAO参数设置Table 6 Software YAO setup parameters

运用差分像运动法结合式，图13给出了L和T两个方向上20次模拟求得的r0计算平均值。

如图13，当S＝2时，无论在L方向或是T方向，本文所用I-DIMM法求得r0值都更接近r0设置值0.03 m的基准线，说明计算结果更精确。计算值分别为0.032 6 m和0.030 3 m，与设置值的误差为8.6%和0.9%，低于DIMM法所得计算值误差10.5%和1.8%。I-DIMM计算得总的r0值为0.031 4 m，误差4.7%，小于DIMM的误差值6.1%。这表明小口径望远镜，子孔径间距分离比S尽管很小，但I-DIMM法求得的总r0值比DIMM更精确。

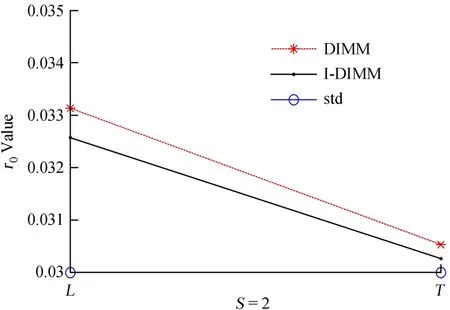
图13 0.12 m望远镜r0计算结果Fig.13 Results of r0 via 0.12m telescope

5 结 语

本文介绍了差分像运动视宁度优化监测法(I-DIMM)在小口径望远镜上，选取一定间距的两个子孔径组合即可计算得到大气视宁度参数r0值。本文通过和传统DIMM对比，在计算公式方面，不但证明了I-DIMM法应用的计算公式在孔径间距为20 cm时计算r0值比DIMM的公式更精确，而且还证明了在孔径间距很小的情况下I-DIMM得到的r0值同样比DIMM更精确，尤其当孔径分离比在1.6～3之间时，无论在沿子孔径中心连线方向还是垂直于子孔径中心连线方向，I-DIMM法计算得到的r0值都比DIMM精确，最大误差在5%左右。在子孔径组合方面，当星像图像数量相同，孔径间距固定时，I-DIMM处理一张图像子孔径信息的组合数大于或等于1，大多数情况下比DIMM处理一张图像只能得到一组子孔径星像偏移信息要多，从而进一步提高了r0计算精度。

本文又通过模拟0.12 m口径望远镜，在孔径分离比为2的视宁度测量情况，进一步验证了IDIMM法计算r0值比DIMM更精确。这就为使用更小口径望远镜提供了证据。同时，I-DIMM只需小口径望远镜上的部分孔径组合，即可求得精确的大气视宁度参数r0，极大地简化了仪器设备，更利于开放环境下便携的大气视宁度测量和选址作业。