插电式燃料电池汽车能量管理在线优化控制策略研究*
2019-01-24应天杏杨林袁静妮孔凡敏周奕
应天杏 杨林 袁静妮 孔凡敏 周奕
(1.上海交通大学,上海 200240;2.上海汽车集团股份有限公司乘用车公司,上海 201804)
主题词:插电式燃料电池汽车 能量管理 在线优化控制
1 前言
燃料电池汽车因其具有零污染、高效率、低噪声的优点,已成为当前国际新能源汽车领域的研究热点[1]。但燃料电池成本依然较高,且其可靠耐久性尚需提高,因此插电式燃料电池汽车(Plug-in Fuel Cell Hybrid Vehicle,PFCHV)成为目前的研发重点。PFCHV采用包含燃料电池系统(Fuel Cell System,FCS)和动力蓄电池系统(Battery Power System,BPS)的混合动力结构,利用BPS高功率(能量)密度和动态响应快的特点,不仅可回收制动能量从而提高整车能效,还能降低对FCS的功率及瞬态特性等性能的要求。但如何分配这两种动力源,使车辆在不同行驶工况下的能效均达到最优,是燃料电池汽车控制中亟待解决的一个关键问题。
国内外学者针对燃料电池汽车的能量管理策略开展了一系列研究。M Pahlevaninezhad等[2]利用查表法与级联控制,使燃料电池和锂电池之间的功率得到有效分配。D.Buntin等[3]设计了基于切换控制的能量管理策略,以保证车辆性能的最优。Zunyan Hu等[4]针对“燃料电池+锂电池”混合动力汽车,设计了多目标能量管理策略,根据锂电池的尺寸采取两种不同的实时控制策略,并通过仿真验证了其有效性。徐梁飞等[5]设计了包括稳态分配和动态补偿两个模块的能量管理策略,并利用遗传优化算法对相关参数进行优化。金振华等[6]根据全局优化结果提取相应控制规则,并设计了基于模糊控制的燃料电池混合动力系统控制策略,从而提高整车的燃料经济性。总结来看,PFCHV的能量管理控制策略仍多采用基于规则的控制方法[7],虽简单易行,但控制规则难于覆盖车辆实际运行中的所有情况,因而无法保证车辆在不同实际道路工况下的能效均达到最优,与最优控制的差异有的甚至高达近20%[8]。而少部分基于动态规划算法等的优化控制策略虽能保证全局最优,但其实时性无法满足车载控制器实际在线应用的要求,只适合于离线优化计算[6]。同时,通过对FCS的研究,发现其与柴油/汽油发动机的动态与稳态运行特性、效率随工况变化的分布特性等均存在显著差异[9],现有混合动力汽车的控制策略无法直接应用于PFCHV。因此,本文通过研究PFCHV能量管理的最优控制规律,提出车辆全程近似最优、短程预测优化和实时优化等3个时空尺度相融合的控制方法,可在实现车辆对不同道路工况开展自适应能量在线优化控制的同时,满足车载控制器对控制策略的实时性要求。
2 车辆动力系统模型
PFCHV的动力系统结构如图1所示。为避免变速器换挡过程引起的动力中断和换挡冲击对车辆驾驶性、舒适性等的影响,系统中仅采用主减速器和差速器实现电机与车轮半轴间的动力传递。

图1 燃料电池混合动力系统
参考文献[10],根据行驶车速v可得主减速差速器输出轴的转速ωDL和转矩TDL:

从而可得电机转矩Tm、转速ωm和机械功率Pm、电功率Pe:
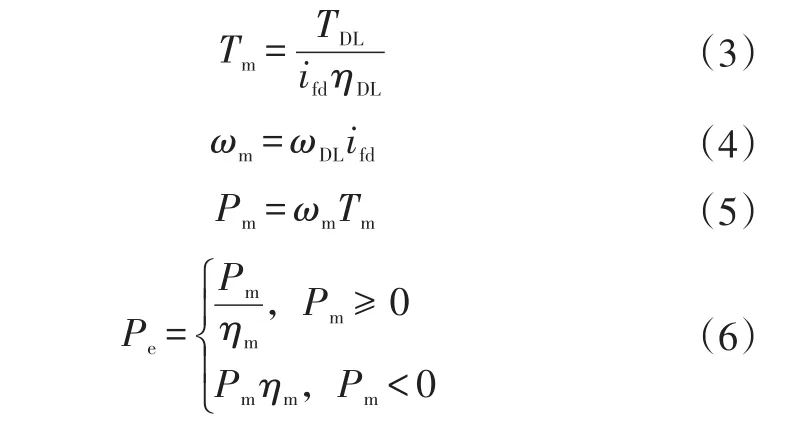
式中,ifd为主减速比;ηDL为主减速差速器的传动效率;ηm=f(Tm,ωm)为电机效率,通过查表计算。
蓄电池系统通过将其等效为一个理想电压源与一个电阻串联的电路来模拟其在充、放电过程中端电压VBP和荷电状态(SOC)的动态过程[11]:

式中,VOC为电池开路电压;IBP为电池电流;R为电池内阻;Pbat为蓄电池功率。
电池荷电状态采用安时法计算:

式中,SOCint为电池初始SOC;QC为电池额定容量。燃料电池系统的氢气消耗率˙H2可表示为:

式中,ηfc=ffc(Pfcs)为燃料电池效率,可通过查表获得;Pfcs为FCS的功率;LHVH2为氢气的低热值。
直流-直流(Direct Current to Direct Current,DC/DC)变换器的输出功率为:

式中,ηDCDC为DC/DC变换器模型转换效率,可查表计算。系统各部件间的功率平衡关系为:

式中,Paux为附件功率。
根据以上公式可构建整车动力系统模型,图2所示为蓄电池模型、燃料电池模型仿真结果与实车道路试验数据的对比,蓄电池SOC和氢气消耗率的均方误差分别为0.001 2和0.002 9。可见,所建立的仿真模型具有较高精度,可用于本文的控制策略研究。
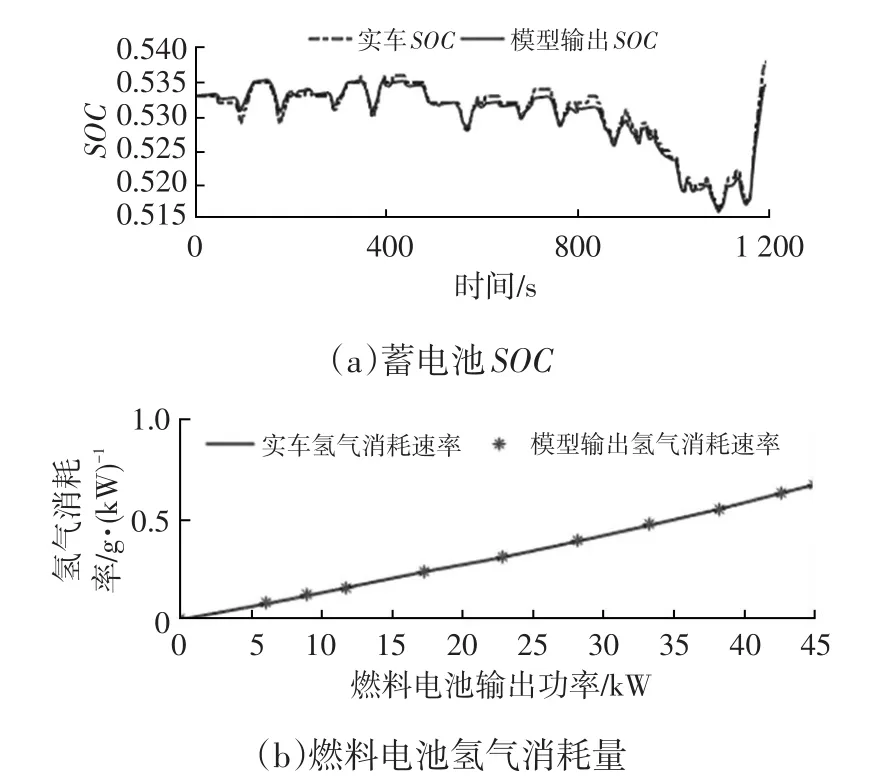
图2 仿真与实测结果的比较
3 能量管理在线优化控制策略
首先建立基于动态规划(Dynamic Programming,DP)算法的PFCHV能量管理最优控制策略的求解算法;然后,针对不同行驶工况,利用最优算法离线探索其能量管理最优控制规律,进而提出面向车-路环境自适应的能量管理在线优化控制方法。
3.1 基于动态规划的能量管理最优控制求解
根据PFCHV动力系统工作过程,定义其燃料电池系统功率Pfcs为控制变量u,蓄电池SOC为状态变量x,则第k步的状态转移方程:
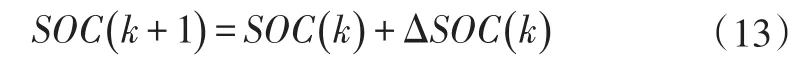
约束条件为:

式中:SOCmin、SOCmax分别为SOC的最小值和最大值;Pfcs,min、Pfcs,max分别为燃料电池输出功率的最小值和最大值;Pbat,min、Pbat,max分别为动力蓄电池的最大充电功率和最大放电功率;Pdown、Pup分别为燃料电池最大降载功率和最大升载功率。
为降低氢气消耗从而降低车辆运行的能源成本,PFCHV需在预设行程终点时使其蓄电池SOC达到预设的下限值SOCCS。因此引入惩罚因子λ,可得每个时间步长内的蓄电池电能消耗Pbat的惩罚值ge:
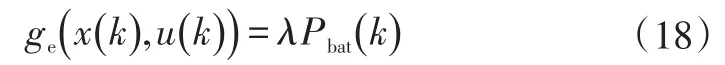
则,优化目标可写为:

式中,n为决策步数;gH2(x(k),u(k))为每个时间步长内的行驶能耗。
调节λ即可获得使SOC满足其行程终点SOCCS需求的Pfcs最优控制序列,采用动态规划算法求解[4,12]。
3.2 全程能量管理控制策略
为了研究PFCHV的全程能量管理控制策略,首先离线开展其最优控制规律研究。为考察最优算法对不同类型、不同距离工况的适应性,进行表1所示42种不同道路工况的测试,包括:UDDS、EUDC等代表中国、欧、美、日等不同地区、不同道路环境的典型工况;本文在上海、苏州等地采集的实车道路行驶工况;为更加充分地模拟车辆实际运行中工况的随机不确定性,进一步测试的这些不同工况的组合工况。其中,高速工况12种、城市工况12种,均含短程、中程和远程工况各4种;组合工况18种,含短程、中程和远程工况各6种。所研究的PFCHV关键参数见表2。研究中,初始时设SOC=0.8,行程终点处设SOC=0.3,对各工况分别采用DP算法求解能量管理的最优控制策略。

表1 不测试工况数量 种
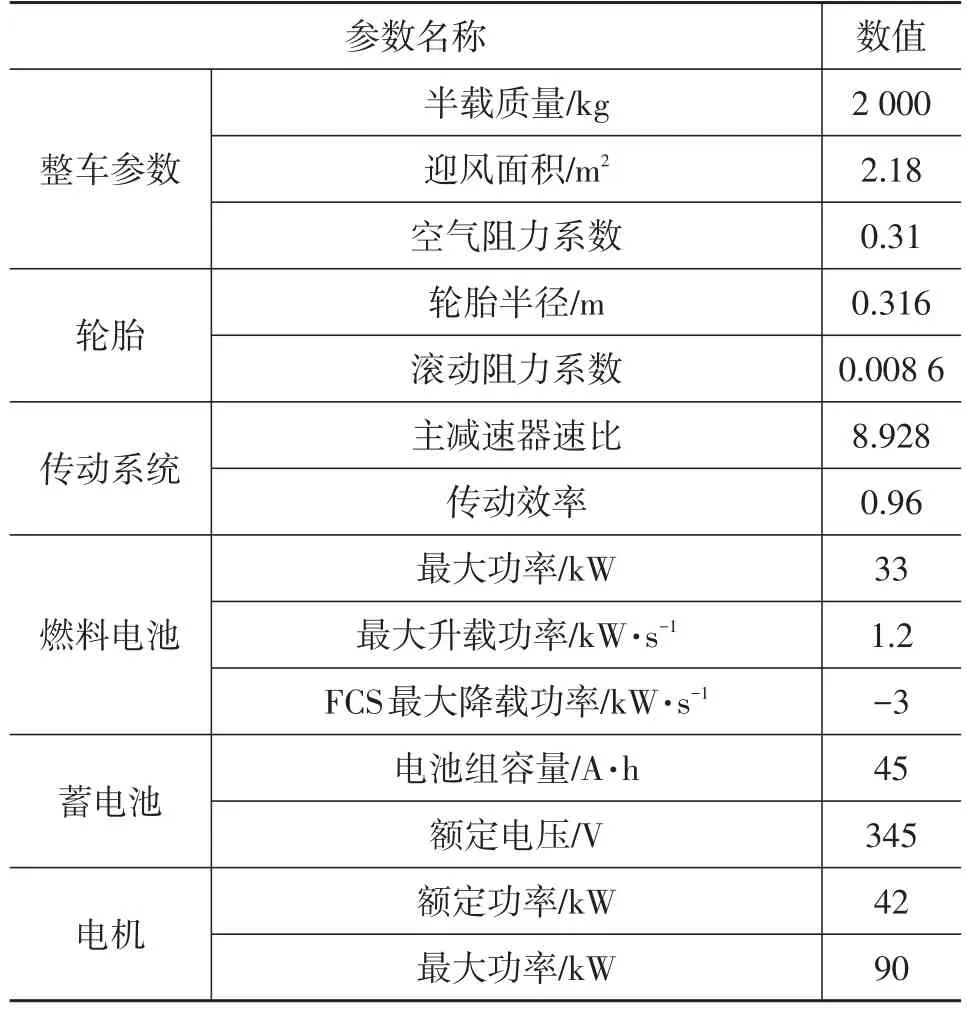
表2 燃料电池汽车关键参数
图3a所示为其中3种行驶工况及相应的最优SOC随行驶里程的变化历程,图3b、图3c分别为从典型、实车和组合工况中随机选取的10种工况的最优SOC随行驶里程的变化历程,以及现有控制系统中常用的电能消耗-维持(CD-CS)控制方法的SOC随里程的变化历程,工况均包含了短程、中程和远程。
由图3a和图3b可见,基于动态规划算法得到的PFCHV最优SOC在车辆行程起点和终点之间均呈近似线性减小的变化规律。这是由于对于PFCHV,一方面,在车辆行驶全程,整车需求功率越大,最优控制的FCS功率也越大(见第2.3节),并不呈现有控制方法中常用的CD-CS控制规律(见图3c),而且受FCS动态响应特性的限制,还存在FCS对BPS充电的情况;另一方面,PFCHV的BPS容量较电量平衡型燃料电池混合动力汽车(FCHV)大许多,短时内BPS电量的消耗并不会引起SOC的较大变化。因此,PFCHV能量管理的最优控制的SOC轨迹与车辆行驶里程的关系可近似为线性:

式中,Dveh为车辆已行驶里程;Dall为车辆预计行驶全程的总里程。
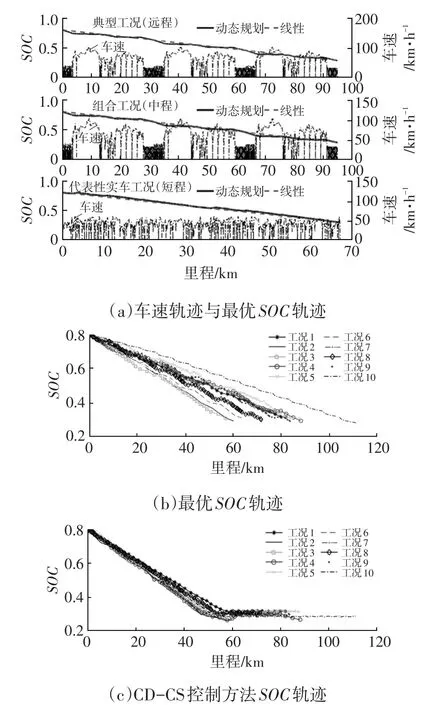
图3 不同工况下PFCHV最优轨迹
对表1的42种测试工况利用DP算法的最优控制策略的统计分析表明:按式(20)的线性轨迹与按DP计算的最优SOC轨迹的绝对偏差的平均值为3.98%、最大值为5.61%;现有常用的CD-CS控制策略的SOC轨迹与按DP计算的最优SOC轨迹的绝对偏差的平均值为9.03%、最大值为15.16%,分别减小了55.92%和62.99%。
这一方面说明对于PFCHV,按式(20)控制SOC,可以开展全程近似最优的能量管理。另一方面,由于工况各片段间的整车需求功率或能量存在差异,受FCS动态响应及其功率-效率特性的影响,按式(20)规划的SOC轨迹与按DP计算的最优轨迹还存在一定的偏差。因此,为进一步减小这一偏差,需要探求基于未来工况片段(即未来短程)与实时的整车需求功率或能量的PFCHV能量管理控制策略。
3.3 基于短程功率预测的燃料电池系统启停控制策略
为实现对SOC与其最优轨迹的偏差提前校正,对测试工况按里程划分为不同小片段,分析每个短程片段内整车需求驱动功率Pdrv与基于动态规划算法的FCS的开启状态、输出功率的相关性。结果表明:其相关性分别达到了0.462和0.512,在0.01水平上显著相关;当片段内的Pdrv较高时,FCS开启,且Pdrv越高则FCS输出功率也越高(见图4)。由此本文提出以片段的平均驱动功率Pavr_drv、实时SOC与式(20)规划的SOC偏差值ΔSOC共同判断燃料电池发动机(Fuel Cell Engine,FCE)的起停状态,如图5所示。其中,Pavr_drv的预测见第4节。

图4 燃料电池系统最优功率与整车驱动功率的关系
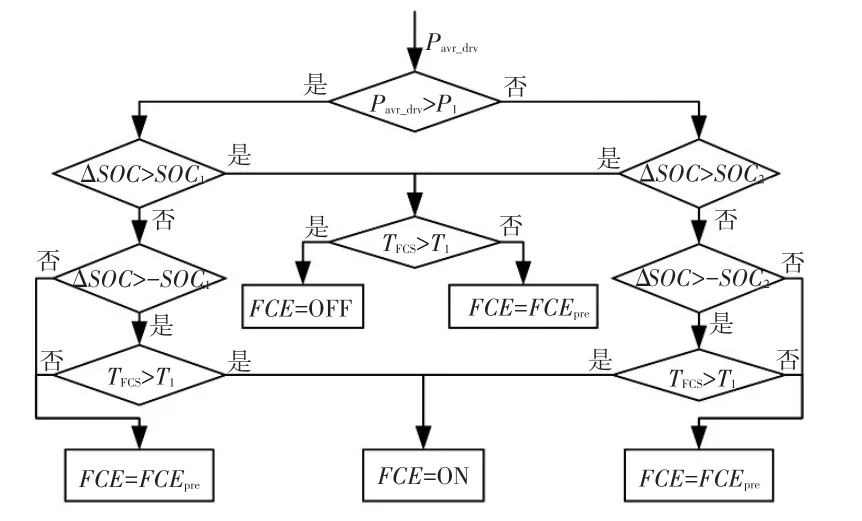
图5 FCS启停判断策略
图5中,P1为平均驱动功率判断阈值,根据DP算法中FCS的开启状态与需求功率的关系统计得到(本文建议设为FCS最大功率的1/3)。通过Pavr_drv与P1的比较,可以选择不同的SOC偏差阈值,即图5中的SOC1与SOC2。根据3.2节的分析,最优SOC轨迹与线性轨迹的最大偏差不超过6%,因此所设的SOC阈值不宜过大,以防止FCE对BPS充电过多,同时SOC1的值应略小于SOC2(本文建议分别取SOC1=0.02,SOC2=0.05)。策略中设置间隔时间T1,可避免频繁启停FCS对其寿命的影响,取值由FCE的特性决定(建议取T1=100 s)。当实际SOC比按式(20)规划的轨迹高出所设阈值时,且间隔时间TFCS>T1,则关闭FCS,采用纯电驱动;当实际SOC比规划的轨迹低出所设阈值时,且已达到冷却时间间隔时T1时,则开启FCS,进行FCS与BPS的多能源混合驱动;否则保持上一时刻FCS的状态,即图中的FCSpre。
3.4 在线优化实时控制策略
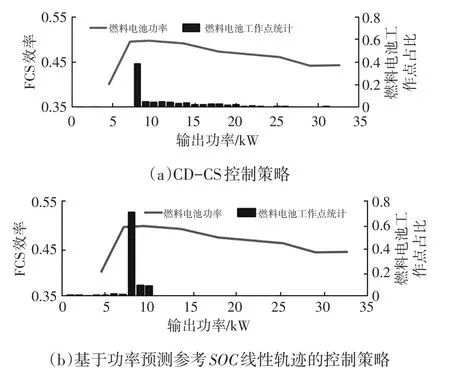
图6所示为全部42种工况FCS最优工作点分布。可见,FCS工作在少数几个稳定功率上,且都在高效工作点功率Pfcs,best附近。这是因为FCS的动态响应特性限制了其输出功率的上升和下降速率,导致其无法像柴油/汽油发动机一样快速变化;同时,为避免FCS启停过程中因氢气-氧气界面高电位等引起的催化剂Pt颗粒脱落,FCS的每次开启或停机过程都只能单向进行。根据此规律,本文提出了能实现PFCHV能量管理的在线优化自适应控制策略,可以使SOC更贴近最优轨迹。该控制策略综合了片段平均驱动功率Pavr_drv、当前时刻的需求功率Pdmnd和ΔSOC来确定FCS的输出功率,其控制策略的流程如图7所示。

图6 燃料电池系统最优工作点分布

图7 FCS输出功率控制流程
首先根据工况片段的平均驱动功率Pavr_drv求得FCS的最大允许工作功率Pwork,max:
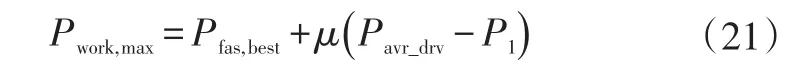
式中,μ为纠正系数,通过统计DP算法下FCS的输出功率与高效工作点的偏差和需求功率的关系得到,本文建议取μ=0.1。
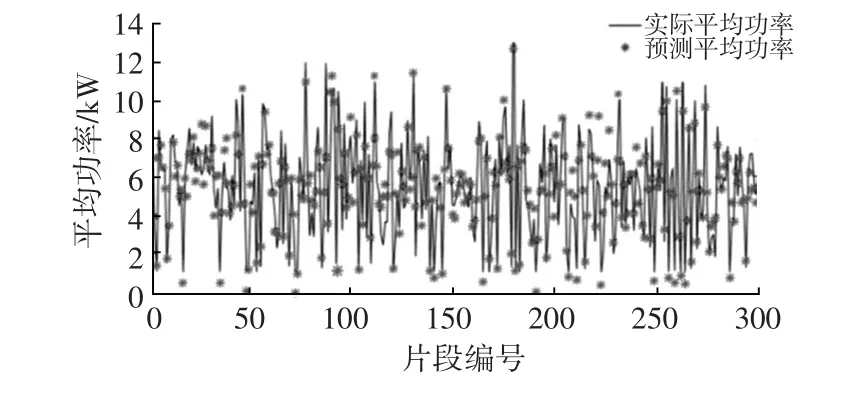
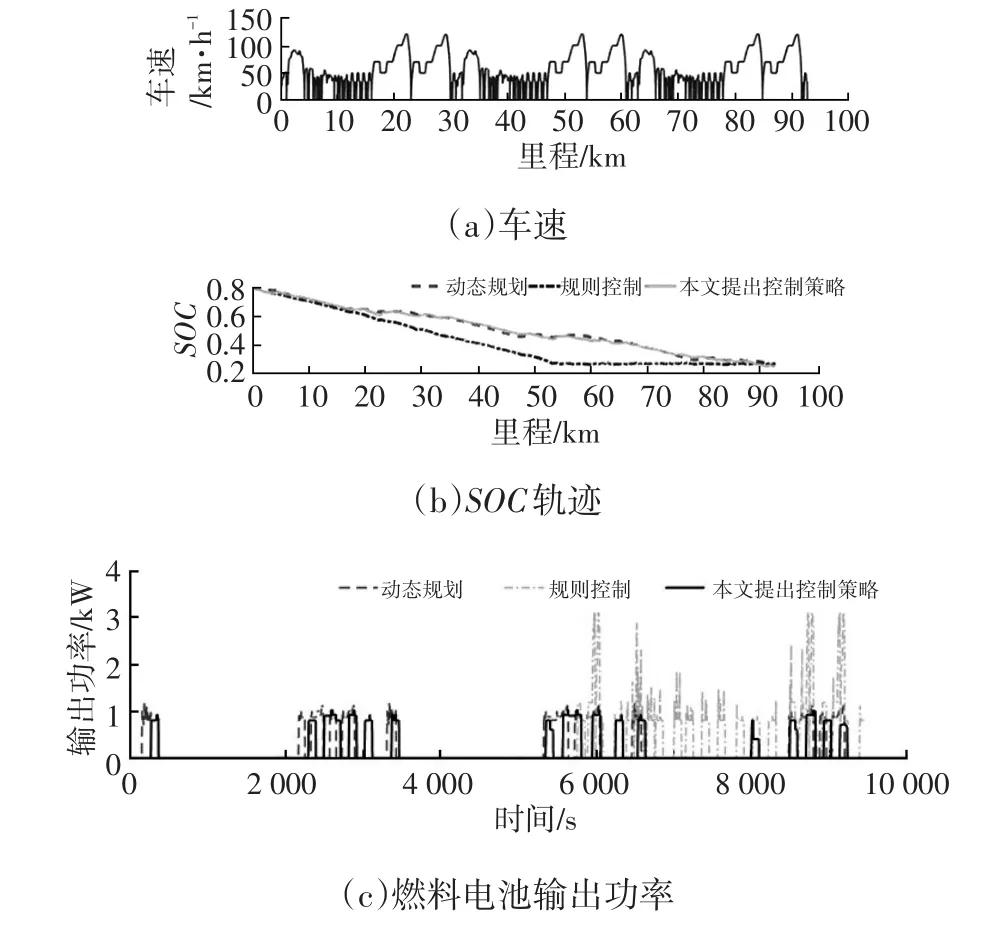
通过提高FCS可输出功率来减小蓄电池电能消耗,使蓄电池电能高效地用于在车辆需求功率较小时的纯蓄电池驱动,从而减少FCS对BPS的充电和FCS低功率低效率运行工况,降低车辆全程的能量消耗。同时,还可在车辆需求功率大时避免蓄电池工作电流过大,延长蓄电池使用寿命。当前一时刻的FCS输出功率Pfcs,pre 在整车控制策略中,需根据未来工况片段的平均驱动功率Pavr_drv来进行优化控制,因此预测未来一段里程内的Pavr_drv成为关键。 由于车辆行驶的能量需求与交通特征直接相关,而径向基神经网络(Radial Basis Function Neural Network,RBF-NN)具有高度非线性的映射能力和很好的泛化能力[13-14],为克服准确预测车辆全程车速轨迹的困难,本文建立基于历史数据驱动的RBF-NN功率预测模型如图8所示,仅通过少量的历史工况特征参数,对长度为S的未来行程进行车辆需求平均功率的短程预测,并通过限定S来保证功率与能量的统一。其中,RBF-NN隐层建议取20个神经元。 图8 车辆平均驱动功率的RBF-NN预测模型 从行驶工况中获取平均车速、车速标准差、怠速时间、加速度等共30个特征参数,通过对历史片段内各特征参数与预测片段的平均驱动功率的相关性分析确定了最大车速、平均功率、功率标准差、不含驻车段的平均车速、加速段平均加速度、行车时间占比、减速段平均减速度、最大车速和片段内平均启停数共9个参数作为RBF-NN的模型输入,模型输出为未来行程S的Pavr_drv。将2/3的工况循环作为RBF-NN的训练数据,余下的作为测试数据来检验模型的准确性。 为了能对车辆行驶中可能的突发情况造成的误差进行修正,从而保证对车辆在实际道路上运行时的随机不确定性工况具有自适应性,模型采用滚动更新机制进行预测,图9所示为基于实车线路采集数据与RBF神经网络预测模型输出结果对比。图10为本文提出的基于功率预测参考SOC线性轨迹的整车能量管理在线优化控制策略的流程。 图9 预测平均驱动功率与实际驱动功率比较 图10 控制策略流程 为评估和验证本文提出的能量管理优化控制策略,本文构建了硬件在环(HIL)测试平台。通过与基于DP离线计算的最优控制结果的比较,来检验控制策略的优化效果。通过对典型工况和实车行驶工况的各种组合,构建了共60条工况进行测试,以验证控制策略对不同工况的适应性。测试中采用按SAE标准换算的等效氢耗来考察不同控制策略的能量管理控制效果。 测试分别采用了CD-CS控制策略与本文所提出的基于功率预测参考SOC线性轨迹控制策略。对某一工况的测试结果如图11所示,CD-CS控制策略优先选择纯电驱动,当SOC下降到SOCCS时燃料电池开启并进行多能源混合驱动,其SOC轨迹与DP算法相差7.93%,等效氢耗高8.17%。本文提出的在线优化控制策略的SOC轨迹更接近于最优SOC轨迹,偏差仅为0.92%;等效氢耗与DP算法相比,仅高2.41%。 图12所示为对CD-CS控制策略与本文所提的控制策略进行的FCS工作点比较。本文提出的控制策略FCS最高效工作点占总工作点的比例为70.48%,而CDCS控制策略最高效工作点占比仅为38.78%。 图11 测试结果 图12 不同控制策略工作点比较 图13为随机选取的20种不同类型工况在不同控制策略下等效氢耗与DP算法的偏差比较。可看出,本文所提的控制策略等效氢耗均低于CD-CS控制策略,说明控制策略具有普遍优越性。 图13 不同策略下等效氢耗偏差比较 表3所示为CD-CS控制策略和本文所提出的控制策略与DP算法的平均SOC偏差、最大SOC偏差、平均百公里等效氢耗偏差和计算耗时的统计结果。可见,本文所提出的控制策略相较于CD-CS控制策略,与动态规划的等效氢耗的平均偏差从9.51%下降到3.68%,同时计算耗时由动态规划的8.2 h缩短到9 ms,在大幅降低等效氢耗的同时,满足了整车控制器在线应用的实时性要求。 表3 控制策略与动态规划结果比较 本文基于对插电式燃料电池汽车能量管理的最优控制规律的研究,提出基于功率预测参考SOC线性轨迹的控制策略,采用基于车辆行驶全程的SOC参考轨迹、基于短程功率预测的FCS在线优化控制及实时优化的自适应控制策略,实现3个时空尺度相融合的联合优化控制。 本文利用RBF神经网络建立的整车驱动功率预测模型,通过少量的历史工况特征参数不仅简化了预测模型,而且能预测出未来一段行驶距离内的平均驱动功率,指导对插电式燃料电池汽车中燃料电池系统的运行控制。 对60种不同工况的测试结果表明,本文提出的控制策略对不同工况具有良好的自适应性;相较于动态规划算法,其百公里等效氢耗平均偏差仅为3.68%、SOC轨迹平均偏差仅为2.47%;并将计算耗时由8.2 h缩短到9 ms,保证了控制策略的实时性。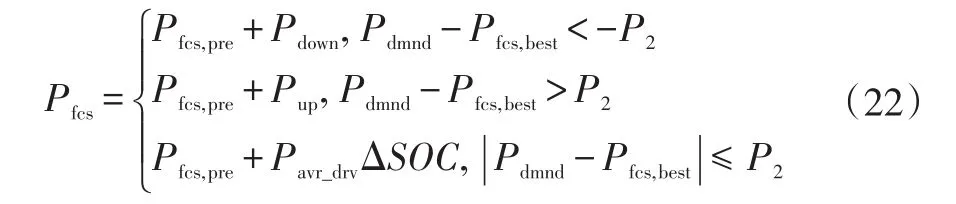
4 整车驱动功率预测模型


5 结果与分析


6 结束语
