让人纠结的箱子

刘金龙

塔塔镇来了一位奇怪的魔法师，他在镇子东头的老槐树下放了两个箱子，说要和镇上的居民们玩“选箱子”的游戏。他的举动引来了镇上的人围观。

魔法师的游戏

魔法师摆放的两个箱子，其中甲箱子是透明的，里面有一枚黄灿灿的金币，而乙箱子是不透明的，里面可能什么都没有，也可能会有一根魔杖。这根魔杖可是很厉害的，可以实现一些愿望，当然了，使用者必须是本着善良的初心。

一切准备妥当，游戏开始了——

参与者有两种选择：一种选择是拿走两个箱子，但当魔法师预测到你会这样做时，他会让乙箱子空着；另一种选择是只拿走乙箱子，当魔法师预测到你会这样做时，他会提前将一根魔杖放进乙箱子。注意，选择的机会只有一次，请慎重考虑。

听完游戏规则，大家便你一言我一语地商量了起来。

“当然是两个箱子都拿走了，至少能得到一枚金币。”

“金币我可不稀罕，我想要魔杖，我只拿乙箱子。”

“只拿乙箱子，如果魔法师预测错误，你将什么都得不到。”

“就是！最好是拿两个箱子。如果魔法师预测错误，我就能得到一枚金币和一根魔杖。”

“嘘！大家别着急，既然是魔法师摆放的箱子，哪会那么容易让我们都拿走。我从隔壁镇亲戚那里听到一个关于魔法师的秘密，他有预测未知的魔力，据说准确率高达90%。”

…………

塔塔镇的居民们在热烈地讨论着，你也别在一旁看热闹。如果你也是游戏的参与者，你会做出何种选择呢？

我也觉得将两个箱子都拿走是比较明智的选择，万一魔法师的预测不准，我还能拿到一枚金币和一根魔杖。

可魔法师预测的准确率高达90%，这个概率很高啊！不过终究不是100%，还是会出现预测错误的可能。

不同选择，不同说法

一番讨论后，很快，塔塔镇的居民们就分成了两拨，因为他们考虑这个问题用了不同的思维方式。

“如果魔法师预测拿箱子的人会将两个箱子都拿走，他就会让乙箱子空着。这时候，拿箱子的人就应该将两个箱子都拿走，这样至少能得到一枚金币。如果魔法师预测拿箱子的人只拿乙箱子，他就会将一根魔杖放入乙箱子。这时候，拿箱子的人更应该将两个箱子都拿走，因为甲箱子里可是有一枚金币呢，它铁定是存在的，没理由放着不要啊！”其中一方代表发了言。

“对，没错！”其他人纷纷附和道。

“反对！”

“反对！”

“魔法师有预测未知的能力，预测的准确率高达90%，那么只拿乙箱子，会有90%的概率能得到一根魔杖。但是如果将两个箱子都拿走，就只有10%的概率能得到一根魔杖和一枚金币。所以，只拿走乙箱子才有最大可能得到一根魔杖。”另一方代表反驳道。

他们的分析都很有道理，到底该拿两个箱子还是只拿乙箱子呢？

又犯迷糊了吧！这就是魔法师的精妙之处，也是数学的有趣之处，继续认真往下看吧。

不管怎么选，矛盾总会出现

对于塔塔镇的居民们来说，无论哪一种选择，他们都想收益最大化。对于他们的选择，我们没办法评判谁对谁错。不过，既然知道了魔法师预测的准确率，那么我们不妨试着用概率知识来分析一下。

当魔法师预测正确时，最好的结果是拿箱子的人得到一根魔杖。而当魔法师预测错误时，最好的结果便是拿箱子的人得到一枚金币和一根魔杖。

当选择拿走两个箱子时，可能会出现两种结果：得到一枚金币或者得到一枚金币和一根魔杖。当选择只拿走乙箱子时，也可能会出现两种结果：得到一根魔杖或者什么也没得到。因为选择拿走两个箱子和选择只拿走乙箱子是两个相互独立的事件，所以，这两种选择发生的可能性都是50%。

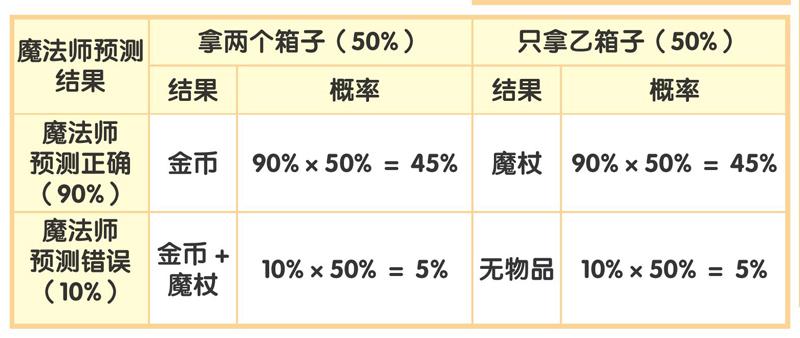
选择拿走两个箱子时，能得到一枚金币的概率是100%，而能得到一根魔杖的概率却只有10%。从整体分析，选择拿走两个箱子的概率是50%，所以，能得到一枚金币和一根魔杖的概率就是5%，而能得到一枚金币的概率是45%+5%=50%。

选择只拿走乙箱子时，能得到一根魔杖的概率是90%，什么都得不到的概率是10%。从整体分析，选择只拿走乙箱子的概率是50%，所以，能得到一根魔杖的概率是45%，而什么都得不到的概率是5%。

根據上述表格数据，如果想获得魔杖，那么我们应该选择只拿走乙箱子，不过放弃了本可以拿到的金币，这与“收益最大化”矛盾；如果拿走两个箱子，魔法师高达90%的预测准确率摆在那儿，也与“收益最大化”矛盾。不管怎么选择，矛盾总会出现，这就是著名的“纽康姆悖论”。

唉，忙活了半天，原来是无解啊！

从分析过程来看，这一切都与魔法师预测的准确率有关。我们不妨试着改变一下这个准确率，看看情况会怎么样。

改变准确率，情况大不同

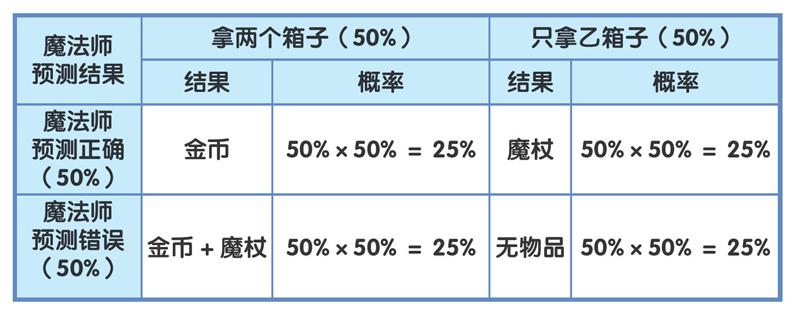
假设将魔法师预测的准确率改为50%，那么选择拿走两个箱子时，能得到一枚金币的概率是100%，而能得到一根魔杖的概率达到了50%。从整体分析，两个事件发生的概率还是各占50%，所以，能得到一枚金币和一根魔杖的概率是25%，而能得到一枚金币的概率还是25%+25%=50%。

而选择只拿走乙箱子时，能得到一根魔杖的概率降到了50%，什么都得不到的概率则上升到了50%。从整体分析，选择只拿走乙箱子的概率为50%，从而得出拿到一根魔杖的概率降为25%，而什么都得不到的概率上升到25%。

这样的话，毫无疑问，当然是将两个箱子都拿走了，因为无论是否拿甲箱子，能得到一根魔杖的概率都是25%，而将两个箱子都拿走还能得到一枚金币。若不拿甲箱子，反而有25%的概率空手而归。

看来，魔法师预测的准确率才是这个悖论的关键所在啊！

之所以为悖论，或许是因为本身给出的一些条件所限制，改变其中的关键条件，也许悖论就不存在了。