基于FLAC3D的煤层开挖流固耦合分析

(西安科技大学地质与环境学院 陕西 西安 710054)

一、引言

我国煤炭资源占国家能源结构的70%以上，“十二五”末期煤炭需求突破40亿t/a。因此煤炭产业在今后相当长的一段时间内都是我国其它产业发展的重要基础[1]。煤矿开采的同时也带了诸多环境问题，其中由于煤矿开采造成当地水位变化在一定程度上破坏了原有的生态环境系统。为了研究煤矿开采过程中当地水位的变化情况，利用FLAC3D数值模拟软件，进行流固耦合分析，得出当地水位在开采过程中的变化及未来的恢复情况。

岩土工程施工阶段对地下水的导流引排作用会改变地下水的原有分布状态，令土体有效应力重分布，而应力场又反过来影响地下水的运动，这种渗流场和应力场之间相互作用，相互影响的现象被称为流固耦合[2]。目前流固耦合理论已在多个领域均有广泛应用。目前流固耦合理论已经运用到土体地下水渗流过程控制、隧道、基坑及相关坝基稳定性分析、地下矿产资源的开发应用、地下水资源的分布等领域[3,4]。李术才等[5]研制了海底隧道流固耦合模型试验系统，对海底隧道围岩应力场与渗流场变换进行了研究，得到了海底隧道施工过程中围岩力学行为和渗流场变化规律。而蔚立元等[6]则对模型试验与数值计算结果进行了对比分析。陈宇等[7]利用有限差分法，以上海市某地铁隧道为例对双圆异性断面盾构隧道土体变形与孔隙水压力分布进行了流固耦合分析，并与实测结果进行比较。

二、FLAC3D流固耦合计算原理

FLAC3D计算岩土体的流固耦合效应时，可以将岩土体视为多孔介质，流体在孔隙介质中流动依据Darcy定律，同时满足Biot方程。该软件使用有线差分法进行流固耦合计算，几个主要方程包括：

(一)平衡方程

对于小变形，流体质点平衡方程为：

(1)

式中，qi,j是渗流速度(m/s)，qv是被测体积的流体源强度(l/s)，ζ是单位体积孔隙介质的流体体积变化量。而

(2)

式中，M是Biot模量(N/m2)，p是孔隙压力，α是Biot系数，ε是体积应变，T是温度，β是考虑流体和颗粒热膨胀系数(1/℃)。

液体质量平衡关系为：

(3)

式中，ζ是液体容量的变分(多空渗水材料中单位体积对液体体积的变分)，qv是液体的密度。

动量平衡的形式为：

(4)

式中，ρ=(1-n)ρs+nρw是体积密度，ρs和ρw分别是固体和液体的密度。(1-n)ρs为基体的干密度ρd(例如：ρ=ρd+nρw)。

(二)运动方程

流体的运动用Darcy定律来描述。对于均质、各向同性固体和流体密度是常数的情况，这个方程具有如下形式：

qi=-k[p-pfxjgj]

(5)

式中，k是介质的渗透系数(m2/Pa·s)，pf是流体密度(kg/m3)，gj(j=1,2,3)是重力加速度的三个分量(m/s2)。

(三)本构方程

体积应变的改变引起流体孔隙压力的变化，反过来，孔隙压力的变化也会导致体积应变的发生。孔隙介质本构方程的增量形式为：

(6)

式中，Δσij是应力增量，Hij是给定函数，εij是总应变。

(四)相容方程

应变率和速度梯度之间的关系为：

(7)

式中，u是介质中某点的速度。

(五)边界条件

在计算中有四种类型的边界条件，分别是：①给定孔隙水压力；②给定边界外法线方向流速分量；③透水边界；④不透水边界。不透水边界在程序中默认，透水边界采用如下形式给出：

qn=h(p-pe)

(8)

式中，qn是边界外法线方向流速分量；h是渗透系数(m3/N·s);p是边界面处的孔隙水压力；pe是渗流出口处的孔隙水压力。

三、数值模型的建立及边界条件

(一)数值模型的建立

模拟研究的地质采矿条件：平均采深为180m，煤层开采厚度为5m，底板厚10m，松散层厚度为80m，为近水平煤层。岩性及力学参数见表1。为了达到煤层充分开采和消除边界效应的目的，将模型走向长尺寸设定为375m。经过模型的多次调试，最终确定设计的开采模型大小为375m×200m×180m，见图1。

表1 岩层力学参数

图1 建立的FLAC3D模型

(二)模拟方案

为了尽可能地与生产实际情况相符合，确定了每次开挖步距为30m，共模拟开挖了300m，并在每次开挖的中心处设置1个测点，共计10个。本次模拟针对每次开挖煤层上覆岩体的竖向位移及孔隙水压力变化进行了记录和研究。

(三)上覆岩体位移变化规律

通过对上述模型进行煤层的开挖模型模拟，分别模拟了煤层开采工作面推进30m，60m，90m，120m，150m，180m，210m，240m，270m，300m时上覆岩体的竖向位移变化规律，其中选取30m，180m，300m的模拟结果如图2～4所示。

(四)孔隙水压力变化

通过对上述模型进行煤层的开挖模型模拟，分别模拟了煤层开采工作面推进30m，60m，90m，120m，150m，180m，210m，240m，270m，300m时孔隙水压力的变化规律，其中选取30m，180m，300m的模拟结果如图5～7所示。

图2 30m开挖位移云图

图3 180m开挖位移云图

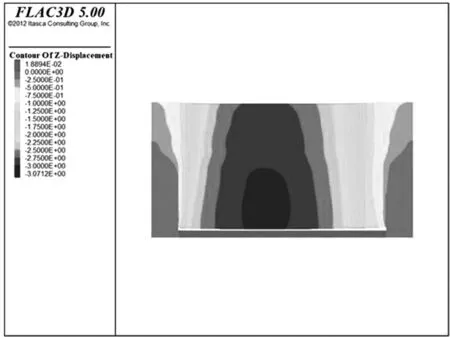
图4 300m开挖位移云图

图5 30m开挖孔隙水压力云图

图6 180m开挖孔隙水压力云图

图7 300m开挖孔隙水压力云图

(五)水位变化情况

通过对上述模型进行煤层的开挖模型模拟，分别模拟了煤层开采工作面推进30m，60m，90m，120m，150m，180m，210m，240m，270m，300m时地表水水位的变化规律，模拟结果如图8所示。

图8 开挖过程中水位变化

为了了解回采后水位的恢复情况，利用软件分别模拟出7d，30d，90d，270d后水位的恢复情况，如图9所示。

图9 回采后水位恢复情况

由图8和图9可以得到相比未回采所造成的水位下降情况，见图10。

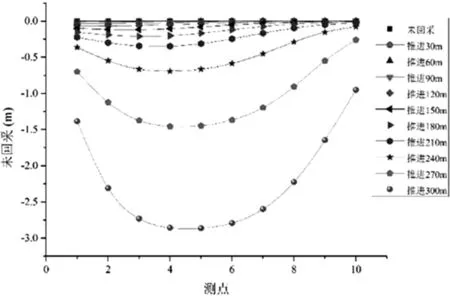
图10 水位下降情况

四、结论

(1)随着工作面的不断推进，地表水水位呈现逐渐降低的趋势，开始时下降的速度较慢，越到开采后期，水位下降的越明显。

(2)回采工作面进行的前期，水位下降最明显的位置集中在已回采距离的中心位置处，而到了回采工作的后期，水位下降最明显的地方则集中在整个模型的中心位置处。

(3)随着时间的不断推移，回采对原水位造成的影响越来越小，不考虑其他外部条件的情况下，大约270天后水位可恢复到原有水平。