基于K-Adaboost数据挖掘的配电网负荷预测

刘 伟，张锐锋，彭道刚

（1.上海电力大学 自动化工程学院，上海发电过程智能管控工程技术研究中心，上海 200090；2.贵州电网有限责任公司电力科学研究院，贵阳 550002）

0 引言

综合目前电力行业的状况，我国提出了“坚强在输电网、智能在配电网”的智能电网发展方针。智能配电网作为智能电网的关键环节，致力于为用户提供更安全、可靠、经济、优质的电力服务[1]，配电网负荷预测作为智能配电网规划和建设的基础和前提，具有十分重要的意义。负荷预测的本质是依据预测对象的历史数据，建立相应的数学模型来阐述其发展规律。

目前，众多学者提出的负荷预测方法可以分为传统方法、智能方法以及传统算法和智能算法相结合的组合算法，其中：传统算法包括时间序列法[2]、回归模型[3]等；智能算法包括神经网络[4]、专家系统[5]等；组合算法有将回归分析与BP神经网络结合构建预测模型[6]等。配电网负荷受诸多随机因素干扰，尤其是气象因素对其造成了直接干扰。对于这些干扰因素，传统预测方法既不能剔除干扰因素，也不能将其考虑到负荷预测的模型中去，因而达不到预测精度的要求。人工智能算法（支持向量机[7]、模糊神经网络[8]等）在进行负荷预测时，可以将诸多干扰因素考虑进负荷模型中。但是配电网负荷是非线性数据，由于人工智能算法不能很好地处理非线性数据，在很大程度上降低了训练速度和精确度。数据挖掘技术不仅能够很好地处理非线性数据，而且可以保留海量数据中有效部分作为训练的样本。

文献[9]提出先将历史数据通过数据挖掘技术预处理，然后使用支持向量机预测系统进行预测。文献[10]使用聚类分析和神经网络相结合构建预测模型。文献[11]针对气象因素对负荷预测的影响，利用数据挖掘聚类分析寻找待测日同等短期负荷数据序列，且使用神经网络预测。支持向量机、神经网络属于有监督学习、参数的设置影响预测精度、泛化能力低，且支持向量机是内存密集型算法，不太适用较大的数据集。K均值算法属于非监督算法，具有灵活性强、效率高等优点，可以处理大量数据。Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练不同的弱分类器，然后将这些弱学习器集合起来，构成一个强分类器，从而提高算法的预测精度以及泛化能力[12]。

基于以上分析，针对配电网的负荷特性结合实时气象数据，提出K-Adaboost负荷预测模型。首先使用K均值算法对待测点气象数据进行分析，从预处理后的历史负荷数据中找到与待测点相近的气象类型，组成具有很强相似气象特征的数据序列作为训练样本，最后再运用Adaboost预测算法进行负荷预测。

1 气象因素对配电网负荷的影响

1.1 气象因素影响下配电网负荷的特点

气候突变前后，通常会伴随负荷的急剧变化。图1所示为某地区温度与负荷之间的曲线关系，图中负荷与温度的关系曲线大致呈倒置的马鞍状。其中，“马鞍”的几个分界点温度即温度与负荷关联的敏感点。在炎热的夏季，负荷对温度最为敏感；而在气温较低的冬季 ，供暖设备运行，配电网负荷也会随着其温度降低而增加。

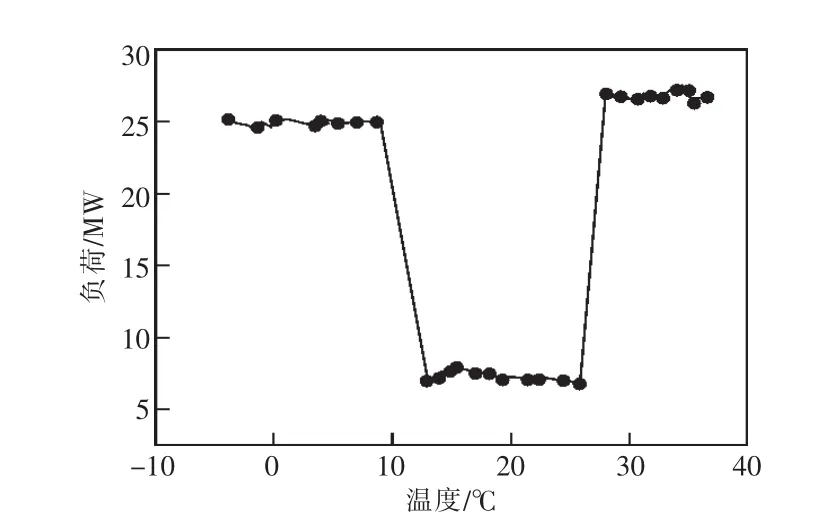
图1 温度与负荷的曲线关系

除温度外，风速、湿度也会对配电网负荷造成影响，如图2所示。其影响规律可以分为4个层次，具体如下：

（1）各气象因素独立作用于配电网负荷，包括2类：单因素分析和多因素分析（各个气象因素不产生耦合现象）。

（2）多个气象因素产生耦合效果再次影响电力负荷。

（3）气象因素的多日累积效应对负荷的影响。

（4）综合气象指数的多日累积效应对负荷的影响。综上所述，气象因素是造成配电网负荷波动的主要原因。

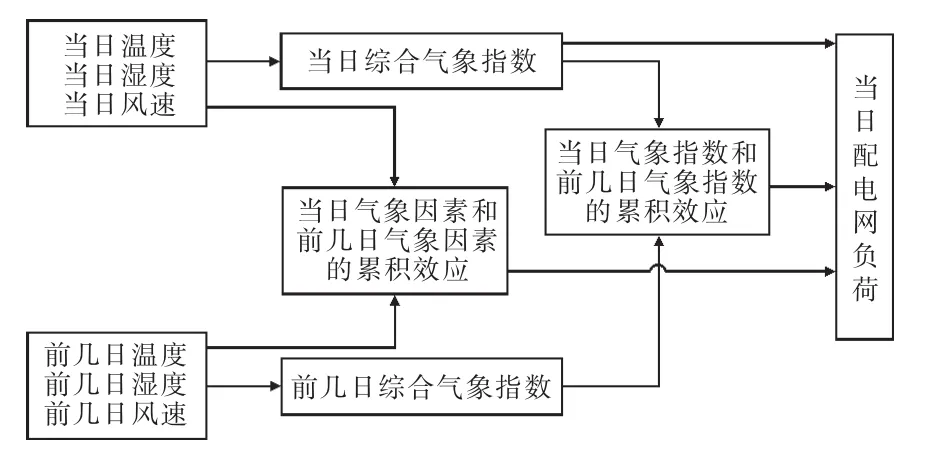
图2 气象因素对配电网负荷的影响

1.2 负荷与气象因素的相关性

从单气象因素和多气象因素2个方面进行负荷预测。采用斯皮尔曼相关系数ρ分析温度、湿度、风速等气象因素与配电网负荷的相关性。

计算该地区的负荷与气象因素的斯皮尔曼相关系数，得到相关性结果如表1所示。由分析结果可以看出，湿度与负荷为弱相关，因此本次研究选择温度和风速作为训练的特征输入向量。

表1 斯皮尔曼相关系数分析结果

1.3 同类气象因素的选择

聚类分析是根据数据相似度进行样本分组的方法。在某种意义下，聚类分析只是其他目的的起点。本文使用K均值算法进行聚类分析。K均值算法[12]是基于原型的聚类技术创建数据对象的单层划分。K均值用质心定义原型，其中质心是一组点的均值。通常，K均值聚类用于n维连续空间中的对象。K均值算法的步骤如下：

（1）将样本数据中的气象数据分为K组，并随机从每组中选取1个作为初始的聚类中心Ci（u），其中 i=1,2，…，K，此时 u=1。

（2）使用曼哈顿距离公式计算每个气象数据xik到各个聚类中心xjk的距离d（i，j），其计算公式如下：

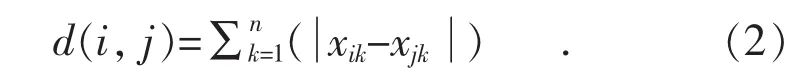
（3）重新计算每组的聚类中心 Ci（u+1）。

（4）若 Ci（u+1）=Ci（u）， 则结束迭代， 此时的中心就是聚类中心； 若 Ci（u+1）≠Ci（u）， 则返回第二步重新进行迭代，直到两者相等为止。

2 预测模型的选择与设计

常用的C4.5决策树、BP神经网络等单一的分类预测算法具有样本敏感性，难以提高分类精度等问题。针对这些问题，现将这些分类算法进行组合。

Adaboost是通过处理训练数据集的方法构建组合分类器[13]。作为一种组合分类器算法，需要一个弱分类作为弱分类器（弱分类器即为基础预测模型），用于单个分类模型的组合训练和结果融合。在选择弱分类器时，应考虑算法的精度和稳定性等多个方面。BP神经网络性能方面已比较成熟，稳定性强，其强大的非线性映射能力符合配电网负载特性，因此在本文选择BP神经网络作为弱分类器。

2.1 弱分类器BP神经网络

BP神经网络具有很强的自主学习和复杂的非线性拟合能力，很适合电力负荷预测问题[14-16]。本文采用多输入单输出前馈型BP神经网络模型，如图3所示。此结构具有很好的函数逼近能力，可以将气象数据（温度、风速）计入预测模型。

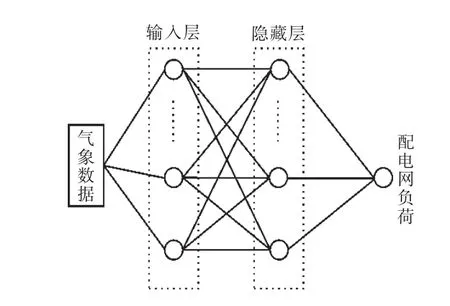
图3 馈型BP神经网络

前馈型BP神经网络由输入层、隐藏层、输出层组成。在前向传递过程中，输入信号从输入层、隐藏层依次传递至输出层，如果输出层达不到期望值，则开始反向传播，根据误差调整网络权值和阈值。

2.2 基于BP神经网络的Adaboost预测算法

Adaboost利用样本的权值来确定其训练集的抽样分析，预测流程如图4所示。首先，将所有样本都赋予相同的权值1/N，因此样本被选作的可能性一样。根据训练样本的抽样分布来抽取样本，得到新的样本集。然后，该训练集归纳一个分类器，并用它对原数据集中的所有样本进行分类。每一轮提升结束时更新训练样本的权值，增加被错误分类的样本的权值，减小被正确分类的样本的权值。迫使分类器在随后迭代中关注那些艰难分类的样本。Adaboost预测的具体步骤为：

（1）从配电网负荷样本中随机选择n个训练数据，初始化测试数据分布权值Dj（i）：

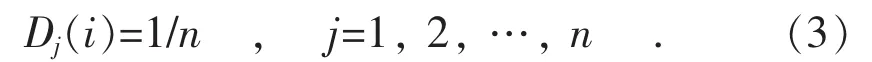
（2）当训练第j个弱类器时，用样本Dj对第j个弱分类器训练并得到训练预测数据，得到预测序列 g（j）的预测误差 εj和权重 αj。 下一轮训练权重α（j+1）根据 αj进行调整。 预测误差εj计算公式如下：

式中：y为期望分类结果。

（3）计算权重 αj公式如下：

（4）根据αi重新调整下一轮训练样本的权重Dj+1（i）， 式中 Bj是归一化因子， gj（xi）为第g 个分类器第i个样本实际输出，yi为第i个样本期望输出。调整公式为：

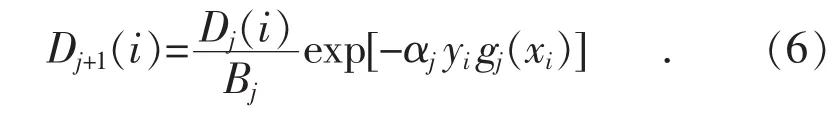
（5）训练 T轮后得到 T组弱分类函数 f（gj，αj）， 强分类函数 C（X）由 T 组弱分类函数 f（gj， αj）组合得到。

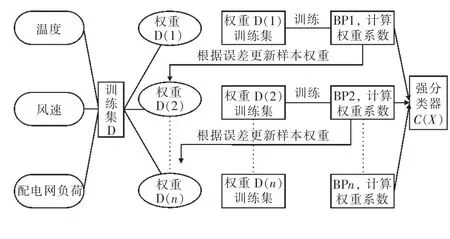
图4 Adaboost预测算法流程

Adaboost算法将每一个分类器Cj的预测值根据αj进行加权，而不是使用多数表决的方案。这种机制允许Adaboost惩罚准确性低的模型。另外，如果超过50%的错误发生，权值将恢复到相同值 Dj（i）=1/n， 并重新进行抽样。

3 建立配电网负荷预测模型

3.1 样本数据的收集与处理

以某住宅楼为研究对象，选择该楼7月21—30日每隔15 min采集1次的数据作为训练样本，对7月31日的配电网负荷进行预测。

配电网负荷在固定季节内呈现周期性变化，一定时间内的负荷具有相似性，且负荷值应该维持在一定范围内。配电网通过SCADA（数据采集与监控）系统采集数据，如果在数据采集的任意一环节受到干扰得到的负荷值超出这个范围，就判断该数据属异常数据。用以下方法修补：

式中：S（d，t）表示第d天t时刻采集的异常负荷值； S（d-n， t）和 S（d+m， t）分别表示异常负荷所在日前n天、后m天同一时刻负荷值；为除异常负荷所在日外其他天数的平均值；S′（d，t）为处理后负荷值；φ（τ）为阈值。

3.2 样本数据归一化处理

为了消除样本中各个数据单位不一样所带来的影响，需对样本数据进行归一化处理，即通过线性变换将原始负荷数据、温度数据、风速数据都映射到[0，1]内，公式如下：

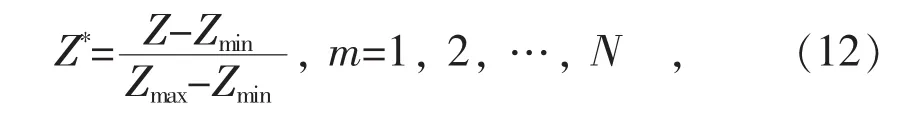
式中：Z表示待转换数据；Zmin表示数据最小值；Zmax表示数据最大值；Z*表示转换后的值。

3.3 弱分类器结构及其参数设置

根据输入输出的维数确定弱分类器BP神经网络结构，从训练样本中选取960组数据作为训练数据，根据数据维数采用的BP神经网络结构为10-6-1，并通过训练产生5个弱分类器，用5个弱分类器组成最终的强分类器。

3.4 预测模型流程

基于K-Adaboost的预测模型如图5所示，首先输入历史负荷数据并进行预处理。在数据挖掘中，数据预处理将真实负荷数据库转换为挖掘数据库。然后将待测点的气象因素（温度、风速）使用K均值算法进行聚类分析，根据聚类分析结果，从预处理后的历史配电网负荷数据中选择同类气象因素作为训练样本。根据样本输入输出维数确定Aadboost算法中弱分类器BP神经网络的结构，然后训练生成弱分类器的个数，最后根据弱分类器个数组成强分类器进行配电网负荷预测。

图5 预测流程

4 案列验证

为了验证K-Adaboost的可行性和准确性，用BP神经网络和K-Adaboost 2种模型预测该楼7月31日配电网负荷，待测点温度和风速数据如图6和图7所示，并通过不同误差表示来进行比较。

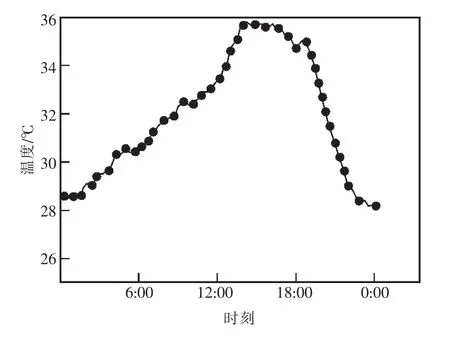
图6 温度数据集

4.1 多因素输入预测结果

将温度和风速同时作为输入因素，得到KAdaboost和BP的预测结果如图8所示，前者的预测结果更加贴近实际负荷，而且更加稳定。BP预测配电网负荷曲线与实际配电网负荷曲线差距更大，而且出现极端情况次数更多。

图7 风速数据集

图8 预测结果

4.2 单因素输入预测结果

分别将风速和温度作为单输入因素进行负荷预测，得到结果如图9和图10所示。可以看到，与多因素输入相比，单因素输入时2种模型的预测结果偏差更大。温度作为单因素输入时得到的结果比风速要稳定且更接近实际负荷，证明了温度对负荷的影响要优于风速。

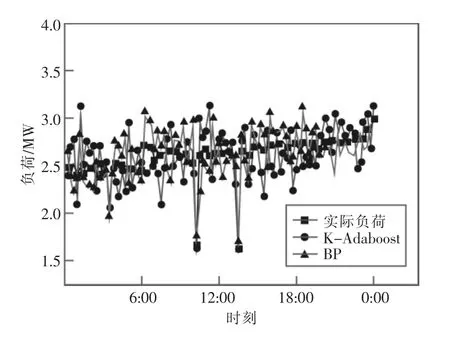
图9 单输入（风速）预测结果

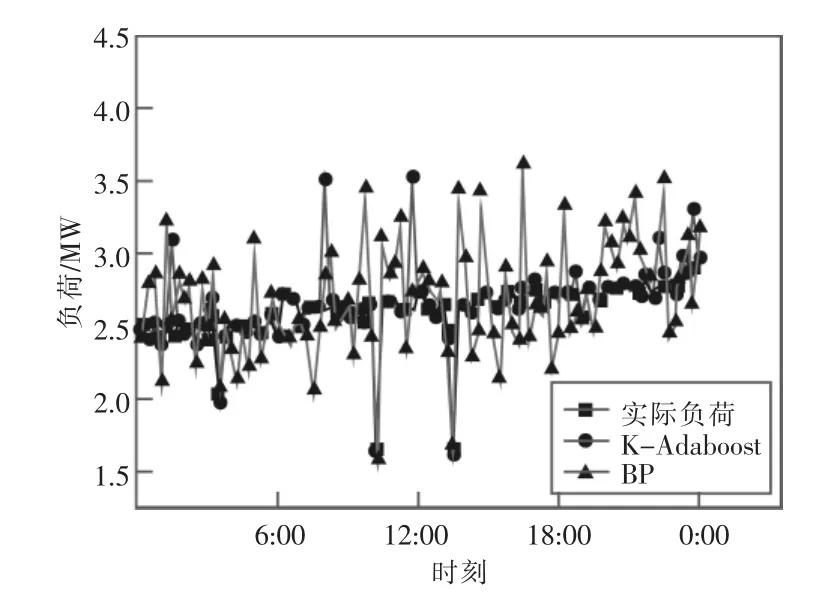
图10 单输入（温度）预测结果

4.3 预测结果评测

为了衡量算法的预测性能，使用了3种统计指标进行评估，分别为均方根误差er、绝对百分误差em、相关系数R2，计算公式如下：

式中： n 为预测时刻； Sc，t-为 t时刻预测负荷； Sw，t为t时刻实际敏感负荷；为预测负荷平均值；er反映模型预测输出值稳定性；em反映预测值偏离实际值程度；R2反映实际值与预测值关联程度。

预测误差结果如表2和表3所示。从表中可以看出，不管是多因素输入还是单因素输入，KAdaboost预测模型与BP预测模型相比较，前者更加稳定、偏离实际程度值低、与实际值关联程度高。比较表2和表3可以看出，多因素输入得到的结果要优于单因素输入，表明配电网负荷受多种气象因素的同时干扰。

表2 多因素误差结果

K-Adaboost预测模型克服了少量样本的不确定性，优化了初始监督学习样本分类不合理的地方，降低总的复杂度。同时有效解决了 BP神经网络容易陷入局部极小值的影响，降低预测误差范围，取得比较好的预测效果。其结果证明该预测模型可以满足配电网负荷这种非线性系统的预测要求。

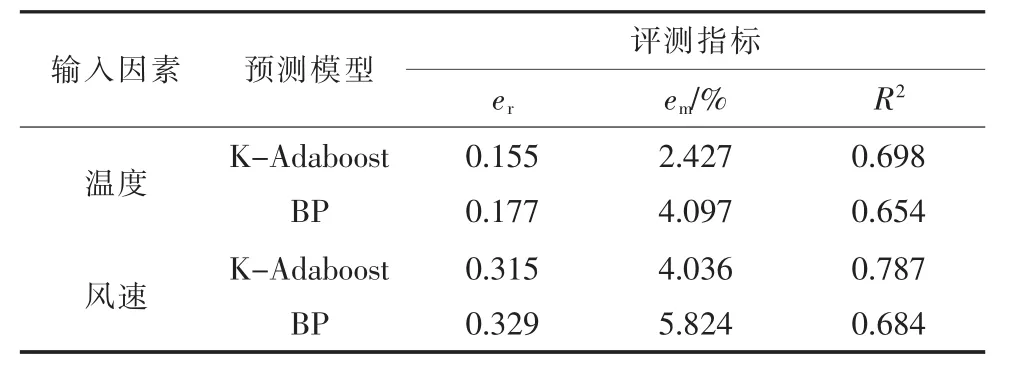
表3 单因素误差结果

5 结语

（1）分析气象因素对配电网负荷的影响，利用斯皮尔曼相关系数得到气象敏感与湿度、温度、风速3个气象因素的相关性。对于本文中未考虑的因素如节假日等，作为下一步继续研究的对象。

（2）用K均值算法对天气数据进行聚类分析，并建立以BP神经网络为弱分类器的Adaboost预测模型。

（3）通过实例证明K-Adaboost预测模型的效果要优于BP神经网络预测模型。