基于CSI的区域粒子化的室内定位算法的研究

宋阳光，殷锋，袁平

（1.四川大学计算机学院，成都610065；2.西南大学计算机科学与技术学院，成都610041；3.重庆大学数学与信息工程学院，重庆400044）

0 引言

近年来，随着无线通信技术的发展以及移动终端设备性能的不断增强，用户对于基于位置服务（Location Based Service，LBS）的需求越来越高。现在的定位主要分为室外定位和室内定位。传统的室外定位系统是卫星定位系统，如全球定位系统（Global Positioning System，GPS）[1]、北斗定位系统。但是对于室内定位来说，由于建筑物密集。遮挡物较多等因素，GPS卫星定位并不能发挥其作用。因此，利用成本低且使用广泛的Wi-Fi技术实现室内定位具有积极的社会意义。

传统的室内定位技术是基于RSSI的三边室内定位算法[2]，但是这种室内定位算法理论上是可行的，但是在实际的应用中，由于测距存在误差，很难建立准确的、低损耗的定位系统[3]。而且，在实际情况下，三圆交于一点的情况很难存在。因此，三边定位算法在实际的实施过程中存在很大的问题。

因此，在本文中，我们提出了基于CSI的区域离子化的室内定位算法。首先，我们使用Wi-Fi信号的信道状态信息CSI来计算定位区域，这样克服了RSSI在复杂室内环境下状态不稳定的缺点。然后我们将定位区域进行粒子化，缩小定位区域，并利用余弦相似度公式得到定位坐标。通过我们最后的实验验证，我们的定位系统达到了分米级的定位精度，与传统的三边定位算法相比有了很大的提升。

1 理论基础

在进行此算法实现之前，先说明一下其中的理论基础。其中一个理论基础来自于三边测量法，其思想是通过三个信号接收器R1，R2，R3，接收通过目标P反射的信号信息，测量出目标P与各个接收器之间的距离d1，d2，d3。然后分别以这接收器R1，R2，R3为圆心，d1，d2，d3为半径做出一个圆，则重叠区域即为目标P的位置坐标。如图1所示。

图1 三边定位

另一个理论基础来源于余弦相似度公式。即对于任意的两个向量来说，可以通过它们之间夹角的余弦值来衡量两个向量的相似度。两个向量的余弦相似度公式为：

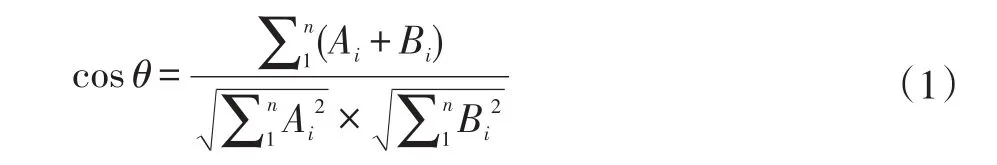
其中，A和B分别是两个向量组，A=(A1，A2，A3，…，An)，B=(B1，B2，B3，…，Bn)。

我们假设有两个节点R1和R2，以及三个已知节点A，B，C。R1相对于 A，B，C 的距离为D1A，D1B，D1C，R2相对于 A，B，C的距离为D2A，D2B，D2C。那么在本文中未知节点R的关系数组可表示为：

relation-array1(DiA，DiB，DiC)，（其中，i=1，2）

根据上面的关系数组公式，节点R1和R2的相关性可以用向量的余弦相似度公式求解，R1和R2的余弦相似度即关系系数可以表示为：

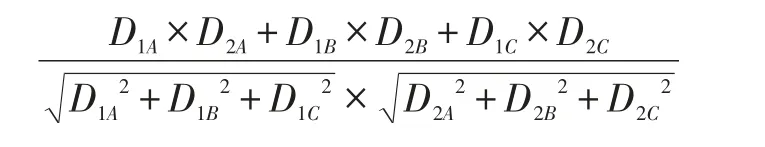
且该系数值越大，节点R1与节点R2位置就越相近。

2 算法实现

2.1 区域粒子化模型

区域粒子化模型的核心思想是对定位区域ABC进行划分，缩小定位区域的面积。为了能够对重叠区域进行合理的划分，可以将曲边看成一条直线，重叠区域就近似成了△ABC，这样对于重叠区域的质心问题就可以转化为求解三角形的质心问题。根据三圆相交公式，我们可以得到交点 A，B，C的坐标A(xa，ya)，B(xb，yb)，A(xc，yc)。利用三角形质心公式，求解得到三角形质心坐标

过质心点O分别连接A，B，C点，将区域ABC分割成三个面积相等的子区域，分别为AOB，AOC，BOC三个区域，然后对这三个区域分别求出每个区域的质心Oi（i=1，2，3）坐标。转化过程如图 2（a）、2（b）和 2（c）。

图2 定位区域转化图

三个子区域的质心坐标分别为：

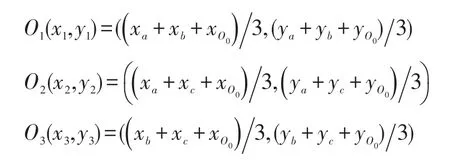
经过上述的区域划分过程，我们将定位区域通过质心平分了三份。接下来，将平分得到的子区域再按照同样的方式进行粒子化划分，将定位区域不断缩小，并求出每个区域对应的质心坐标。最后，我们能够得到一个定位区域的粒子区域的质心分布图，区域粒子化模型如图 3（a）和 3（b）：

图3 区域粒子化模型

根据三角形质心公式我们可以得到粒子区域的质心 坐 标Oi(xOi，yOi)。 我 们 可 以 根 据 公 式得到粒子区域的质心坐标与Wi-Fi信号接收器之间的距离dij。其中，i∈[1，2，3，4…]，jϵ[1，2，3]。由此可知，可以根据质心各个粒子区域的质心坐标建立质心的关系矩阵：

（di1，di2，di3）n×3其中iϵ(1，2，3…n)

对于未知节点P来说，虽然说其是未知的，但是，通过接收端AP1，AP2，AP3可以获取节点P的信号，并且可以根据以下的信号衰减公式获取得到P点信号强度：

Pri=Pt-10γlogdi其中 i=1，2，3

其中，Pt表示Wi-Fi信号发射端与接收端相距1m的信号强度，Pri表示Wi-Fi信号接收器i接收到的信号强度，γ表示Wi-Fi信号传播环境的路径损耗系数。

2.2 相似度匹配算法

根据我们已经得出的P点的关系数组，使用余弦相似度公式计算P点的关系数组与粒子区域质心点的关系数组的关系系数。重叠区域ABC经过区域粒子化过程，得到的子区域面积相对较小，在该区域任意位置接收到的信号所受到的干扰可以看成是相同的，那么本文认为信号衰减模型公式表示的未知节点P与AP节点的距离与子区域质心节点与AP的距离的相关性是合理的。那么根据公式（1）和三圆相交的圆心方程，P的关系数组与子区域质心点的关系系数可以表示为：

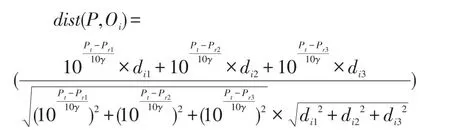
其中 i=1，2，3，…，dia表示第 i个质心点与接收器 a之间的距离。

未知节点P与粒子区域质心点的关系系数越大，它们的位置就越接近。由于我们将重叠区域ABC经过区域粒子化后，每一个粒子区域面积很小，可近似将粒子区域中的质心信息看作此粒子区域的信号信息。则未知节点P在关系系数最大的质心点对应的区域中，质心点位置可以近似为P的位置。综上，利用CSI的区域粒子化，可将重叠区域面积逐渐缩小，并通过余弦相似度估计未知节点P的坐标（xoi，yoi）。

3 算法验证与实验分析

为了能够对本文提出的区域粒子化的室内定位算法进行评估，本文选用了一个20m×15m的教室作为实验环境来获取CSI数据。在教室内放置一个普通的商用Wi-Fi设备作为信号发射器，我们采用ThinkPad X40，配备便宜的现成的Intel 5300 Wi-Fi卡作为信号的接收器，接收器由一组3根接收天线组成，分别分布在教室内不同的位置来获取Wi-Fi信号。并且，我们将Halperin开发的CSI工具[4]安装到我们的实验电脑上，以收集每个接收器接收到的数据包的CSI样本。图4显示了实验环境的设置。

图4 实验环境

在图4中，AP是商用路由器，用于发射Wi-Fi信号，Rx是三根信号接收器，分别放置于室内不同的位置，P是室内的待定位的运动的人。我们实验中CSI的采样率设置为200Hz，以确保人体运动引起的所有多普勒率都能够被检测到，因为室内环境中的人体速度通常小于3m/s[5]。为了避免干扰，我们的实验是带宽20MHz的未使用的5GHz频段内进行的。

在实验中，我们为了能够更好地计算出本文提出的室内定位算法的精确度，我们在实验环境中安装了一个摄像机用于记录人的行走时间与位置的对应关系。然后我们让5名志愿者在不同的时间段，沿着不同的运动轨迹进行运动，例如直线、矩形、圆形等。然后我们为每一个志愿者收集270个运动数据，并报告行人的实时的定位数据以及定位误差。图5（a）和5（b）是系统定位结果的例子。

在上述的两幅图中，红色点是摄像机拍摄到的定位的位置，即为行人的实际的运动位置，而黑色的点是系统采集CSI数据，并计算得出的定位位置。通过观察我们可以发现，本文的算法系统对于行人的室内定位存在一定的误差，通过对5名志愿者进行三周的实验数据采集，我们得出了区域离子化的室内定位算法平均误差在0.85m，达到了亚米级的室内定位精度，相比传统的基于三边定位原理的室内定位算法有了很高的提升精度。

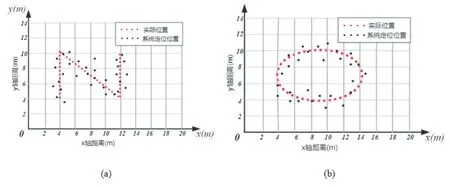
图5 系统定位结果

为了获得对于区域划分度n以及粒子区域面积A与定位精度之间的关系，我们通过实验，收集300个运动数据，计算并得出了定位重叠区域划分度n与定位精度之间的关系以及划分得到的粒子区域面积A与定位精度之间的关系。如图6所示。

图6 区域粒子化度与定位精度的关系

通过图6和图7可以观察到，定位精度随着定位重叠区域的划分度的逐渐增加而增加，当划分度n=4时，定位精度趋于稳定。而且定位精度随着粒子区域面积的减小而逐渐增加，当粒子区域面积接近0.1m2时，定位精度趋于稳定。在第二节中我们已经知道，粒子区域的划分与质心相关，划分度每增加1，粒子区域就会划分成3个面积相等的子区域。因此，我们可以得出这样的结论，重叠的定位区域的粒子化的过程，将重叠区域不断的划分，直到将粒子区域面积划分成接近0.1m2时。这样，我们就可以降低系统复杂度，并获取比较高的定位精度。

图7 区域粒子化度与粒子区域面积的关系

4 结语

本文我们为室内定位提出了一个新的室内定位算法，称为基于CSI的区域离子化的室内定位算法。该算法是通过收集人体运动引起的CSI变化信息，计算出人的定位区域，然后将定位区域不断的划分，缩小定位区域面积，并利用余弦相似度匹配获得更高的定位精度。与传统的基于RSSI的三边定位算法相比，不但更适用于复杂的室内环境，而且在定位精度方面有了更高的提升。