基于多因子模型的股市赌博偏好收益分析

摘   要：近年来，股票市场一直是我国金融风险凸显的主要领域，而投资者赌博偏好正是导致我国股市波动的重要原因。运用多因子定价模型和两阶段横截面回归，对有限理性下“错误定价”与风险偏好下“风险承担”对股市投资者赌博偏好及其负异常收益的影响机理进行检验。实证结果表明，利用最大日收益率构建的赌博因子能够解释股票收益，并与赌博特征的收益解释能力正相关。进一步利用两阶段横截面回归发现，赌博特征能够控制赌博因子载荷的收益解释能力，赌博型收益源于赌博型股票的错误定价。这意味着我国股市投资者的赌博偏好是一种有限理性的表现，并非出于某种风险承担。

关  键  词：赌博偏好;赌博型收益;风险偏好;有限理性

中图分类号：F832.5     文献标识码：A      文章编号：2096-2517（2019）06-0030-12

DOI：10.16620/j.cnki.jrjy.2019.06

.004

一、引言

近年来，股票市场一直是我国系统性金融风险凸显的主要领域，而投资者赌博偏好正是导致和加剧我国股市波动和资产泡沫的重要原因[1]。事实上，股市投资者的赌博偏好早已引起学术界和业界的广泛关注。投资者对收益正偏的“赌博型股票”的热捧导致显著的赌博偏好。目前，相关的国内外研究已经表明，赌博型股票表现出负异常收益[2-11]，即收益率无法用经典资产定价模型解释。赌博型股票的收益行为正是投资者赌博偏好的市场表现。 因此，在Kumar（2009）投资者赌博偏好不可直接观测的观点下[2]，分析赌博型股票的收益成因，有利于各界对投资者赌博动机的理解，进而有助于防范化解系统性风险。

从理论分析来看，国外Brunnermeier等（2007）、Barberis等（2008）认为“错误定价解释”是投资者因为偏好正偏性的股票收益分布，进而导致赌博型收益[12-13]。因此，这一解释也被称为“偏度偏好假说”。Zhong等（2016）认为“风险承担解释”是赌博型收益源于错误设定的定价模型，遗漏了某一能够控制赌博型收益的定价因子[14]。

国内研究对赌博型收益成因的解释大多源于国外研究中的有限理性错误定价理论。譬如，崔惠颖（2019）认为关于赌博型收益的成因解释，具体分为有限理性下的“错误定价”和风险偏好下的“风险承担”两个视角[15]。陈文博等（2019）[16]、崔惠颖（2019c）[11]、徐小君（2010）[17]认为中国股市投资者高估赌博型股票，并导致较低的未来回报。郑振龙等（2013）认为过度自信等行为偏差致使投资者高估赌博型股票获得巨额回报的可能性，从而偏好于赌博型股票[5]。

从实证研究方面来看，国内外研究均没有对赌博型收益的有限理性成因进行实证检验。更重要的是，绝大多数研究忽略了“风险承担解释”。以往研究普遍认为赌博型收益源于股票错误定价，并意味着理性因子定价模型的无效性，却没有详细考察是否存在更好的风险定价因子可以解释赌博型收益。但是一个严谨的研究逻辑是， 我们应该综合性、系统性地检验“错误定价”与“风险承担”对投资者赌博偏好及其收益结果的影响机理。

检验收益率异象成因的经典方法是利用多因子定价模型，将可能反映这一收益率异象的风险原因的备选因子加入到CAPM模型或Fama-French三因子模型中，来判断该风险因子是否具有定价功能。不过，该方法选择出的定价因子也有可能是源于其他非风险原因。 为了解决这一问题，Zhong等（2016）[14]、Core等（2007）[18]和Hirshleifer等（2012）[19]在检验某一收益率异象的成因过程中，进一步结合两阶段横截面回归（Two-stage Cross-sectional Regressions，2SCSR）来识别因子的定价能力究竟源于风险承担，还是其他非理性因素。

为了更全面、清晰地检验股市投资者赌博偏好的收益成因，本文借鉴Zhong等（2016）[16]、Core等（2007）[18]以及Hirshleifer等（2012）[19]对收益率异象的研究思路，利用两阶段横截面回归和多因子定价模型，基于适用于中国股市的赌博因子，通过区别赌博风险定价和赌博特征定价，来综合检验赌博型收益的“风险观解释”和“错误定价解释”。

与已有研究相比，本文的主要贡献在于：（1）构建了适用于中国股市的赌博因子， 根据崔惠颖等（2016），适用于中国股市赌博型股票的最优识别指标是最大日收益率（MAX）和特质偏度（IS）[8]。此外，还发现MAX与特质波动率（IV）具有较高的相关性;IS与预期特质偏度（EIS）的相关性较高。为此， 本文以识别效果最好的MAX指标为主， 构建了IV中性的MAX赌博因子，进行相关检验。同时，将EIS中性的IS赌博因子相关分析作为稳健性检验，以保证结果的稳健性。（2） 本文对赌博型收益的成因檢验并不局限于“风险观解释”和“错误定价解释”中某一个，而是在一个框架内综合检验赌博型收益究竟源于风险偏好还是有限理性。（3） 结合多因子定价模型和2SCSR方法， 避免单一方法无法区别赌博风险定价和赌博特征定价的劣势。

二、数据选取与变量计算

本文所用数据为沪深A股交易数据， 并剔除了PT、ST、IPO以及复牌的股票样本， 以控制涨跌停板制度的影响。同时，为了保证赌博型股票识别指标的有效性，只有交易月份在6个月以上、月交易次数在15天以上的数据才能选入样本。样本数据始于1999年3月，共计197个月。主要变量有：（1） 赌博型股票的识别指标， 包括最大日收益率（MAX）、特质偏度（IS）、特质波动率（IV）、预期特质偏度（EIS）;（2）多因子定价模型所用变量，包括个股月收益率、Fama-French三因子;（3） 控制变量，包括公司规模（Size）、账面市值比（BM）。所有数据均来自锐思金融研究数据库（RESSET） 和国泰安CSMAR系列研究数据库。其中，赌博型股票识别指标的含义与计算方法如表1所示。

三、研究方法与研究步骤

（一）研究方法

本文使用的两个核心方法分别是多因子定价模型和两阶段横截面回归（2SCSR）。其中，2SCSR是基于两步法，来判断某一备选变量是否为定价因子，以及检验该因子定价能力的原因。具体而言，首先，基于收益率异象构建相关备用因子变量，基于多因子定价模型，利用股票和各因子的时间序列数据来估计各定价因子的Beta值;然后，进行横截面回归检验各定价因子的风险溢价情况，核心解释变量即为得到的Beta值。这意味着，2SCSR所使用的因子载荷是估计值，而不是实际值。由于Beta值是不可观测的理论概念（潜变量），因此只能利用其估计值来作为代理变量。

变量误差（Errors-In-Variables，EIV）问题可以由于估计值的引入而出现，也就是所使用的估计值可能导致了测量误差。这一误差可能令普通最小二乘（OLS）的估计量是有偏的，并且伴随标准误的不一致。在多元回归模型中，测量误差所引起的估计偏差方向是不可预测的，最终导致检验结果的错误判断。为避免两步法可能产生的EIV问题，本文将借鉴Fama等（1992）[22]采用的分组法对此进行修正。

（二）研究步骤

为了系统分析股市投资者赌博偏好的收益成因， 本文将结合多因子定价模型和2SCSR方法检验有限理性下“错误定价”与风险偏好下“风险承担”对赌博偏好负异常收益的影响机理。具体实证研究逻辑是：首先，基于恰当的赌博型股票识别指标，构建适用于中国股市投资者的赌博因子;其次，分别将样本按照股票的赌博特征和其他控制变量分组， 在Fama-French三因子模型中加入賭博因子;最后，利用2SCSR进一步分析赌博型收益的成因。 以剔除了特质波动率影响的MAX识别指标为例，具体说明研究步骤：

1. 构建IV中性的赌博因子MAXfactorIV。首先，每月分别按照MAX和IV指标的大小，将样本股票排序等分为3组和2组，共计6个组合。其次，计算各组合的次月收益。再次，计算剔除IV影响的赌博因子MAXfactorIV。

2. 进行组合的三因子和四因子回归分析①。对比三因子和四因子模型的回归结果，若加入赌博因子能够提高回归的调整R2， 降低截距项拟合值和显著性，并且赌博因子载荷显著，则说明加入的赌博因子能够解释股票收益率。 不过，Hirshleifer等（2012） 指出， 我们无法区分这一结果源于赌博特征，还是源于赌博风险定价[19]。为此，本文对比四种不同的分组方式，以考察赌博特征定价和赌博风险定价。

3. 利用2SCSR方法检验赌博因子是否为定价因子。首先，构造组合。利用式（1）滚动估计个股每月的四因子系数（即因子载荷）;先依据MAXfactorIV的载荷大小将股票平均分为3组， 然后按Size、BM和MAX分别进行三等分，共81个组合。

Rq，t-RF，t=？琢+？茁q，MKT（RM，t-RF，t）+？茁q，SMBSMBt+

？茁q，HMLHMLt+？茁q，MAXfactor■MAXfactorIV，t+

？着q，t     （1）

其中，被解释变量为组合超额收益，解释变量分别是市场风险溢酬、规模因子、账面市值比因子和赌博因子，？茁q，MKT、？茁q，SMB、？茁q，HML、？茁q，MAXfactor■为各因子载荷。

其次，对四个因子进行时间序列回归，基于之前24个月的组合收益， 可以得到每个月的组合四因子载荷。

再次，将各因子载荷作为解释变量，各个月进行一次回归，计算系数估计量的均值，并检验系数均值的显著性。

若赌博因子载荷的系数显著，说明赌博型收益可能源于模型误设。 进一步将赌博特征变量MAX加入模型，若MAX的系数显著，同时赌博因子载荷的系数变得不显著， 则说明模型误设只是表象，赌博型收益其实源于股票错误定价。

四、实证分析

（一）四因子描述性统计分析

在Fama-French三因子基础上，本文基于赌博型股票收益率构建了IV中性的赌博因子MAXfactorIV，表2为四因子的描述性统计分析和相关性分析。由表可知，本文的关键因子MAXfactorIV均值为0.0080，方差为0.0009，t值为3.71，通过了显著性检验，说明构建的赌博因子是有效的。在其他三个因子中， 市场溢价因子MKT的方差为0.0077，波动性最大。MKT和SMB均通过显著性检验，仅有HML的t值较小，意味着HML在中国股市并不显著。 另外， 表2显示赌博因子与Fama-French三因子的相关性较低，本文构建的赌博因子不能被三因子所包含，有效性较好。

（二）全样本期的多因子模型检验

在整个检验期内，按照第三部分介绍的分组方法，形成一系列股票组合，然后对各组合进行多因子模型回归如表3所示。 表3是将所有样本按MAX大小等分为10组，分别拟合Fama-French三因子模型和加入赌博因子的四因子模型回归结果。其中，由组合1～10，各组合股票的平均MAX值递增，即股票的赌博特性增强。

重点考察表3中各组合的拟合优度、常数项的显著性以及赌博因子的显著性。首先，赌博因子的引入使各组合的拟合优度有不同程度的提高。其中， 组合1～3、8～10的拟合优度改善幅度最大，而中间组合的改善幅度相对较小，即股票赌博特征表现出明显的非线性变化。具体而言，组合1在加入MAXfactorIV前后的三因子模型和四因子模型回归中，其R2值由91.20%提高至95.51%，改善幅度为4.73%;组合10的R2值则由90.52%提高至95.16%，改善幅度达到了5.13%。整体来看，各组合的调整R2在加入赌博因子之后均超过95%， 说明赌博因子对股票截面收益具有很好的解释力。

其次，在常数项方面，股票的异常收益及其显著性均有所降低， 且表现出与R2值相似的变化规律。类似地，两端组合的常数项的拟合值和显著性变化更大，而中间组合的变化相对较小。例如，组合10的常数项拟合值和t值在加入MAXfactorIV之后， 分别由-0.0096和-4.03提高至-0.0031和-1.77;组合6的常数项拟合值和t值则由0.0020和1.37变为0.0020和1.31，几乎没有变化，再次证明了股票赌博特征的非线性。

第三， 在赌博因子的显著性方面， 绝大部分MAXfactorIV系数均十分显著。由表3可知，在10个组合中，有8个MAXfactorIV系数的t值绝对值远远大于2。更重要的是，各组MAXfactorIV系数的拟合值及相应t值所表现出的变动趋势是：（1） 两端组合的MAXfactorIV系数t值绝对值最大，并且取值的绝对值十分相近，而中间组合的最小，甚至博彩因子的系数不显著，呈现U型变动。例如，组合1的赌博因子系数t值为13.42，组合2为10.56，均十分显著。组合10的赌博因子系数t值为-13.41，组合9为-10.42。至于中间组合，如组合5、组合6的赌博因子系数t值分别为1.88、0.02，赌博因子系数并不显著。（2） 各组MAXfactorIV系数的拟合值及相应t值均随MAX值的增加而增大， 表现出明显的由正变负的趋势。这一重要特征说明赌博特征与赌博因子载荷具有一定相关性，间接说明赌博因子对股票收益的解释力可能源于赌博特征，或者赌博因子未能充分控制住赌博特征对股票收益的影响[19]。

为了同时控制赌博特征和公司特征对回归产生的可能影响， 本文将样本股票分别依据公司规模、 账面市值比和MAX值排序等分为5组，共计125个组合， 再次进行三因子和四因子回归如表4所示。 表4仅列示了各维度两端组合的检验结果，其中8个MAXfactorIV系数拟合值中有7个显著。同时， 结果显示，MAXfactorIV系数拟合值随着Size和BM两个维度上的变化，仍然呈现出明显的由正变负的变化趋势。总而言之，由上述全样本期的检验结果可知，赌博因子对股票收益具有较好的解释能力，这一初步结果看似支持了风险偏好视角下的“风险承担”假设。然而，通过控制变量分组法，可以发现赌博因子的收益解释能力很有可能是源于股票的赌博特征，同时赌博特征对股票收益的影响没有被赌博因子所涵盖。对于这样的检验结果，有必要进一步结合2SCSR方法来深入识别赌博型收益的成因来源。

（三）基于分组法的定价检验

前文已经证实赌博因子对股票收益具有良好的解释能力，不过这一能力可能源于其与股票赌博特征的相关性。因此，仅通过上述检验还不能准确判断赌博型收益究竟源于风险承担视角下的模型误设，还是源于有限理性视角下的错误定价。本文将进一步采用基于分组法的两阶段横截面回归（2SCSR）来检验赌博型收益的成因，其核心逻辑是先控制住MAX的影响，然后考察赌博因子载荷是否仍具有股票收益的解释能力。 如果MAXfactorIV是资产定价的系统性风险，那么在对赌博因子载荷继續回归时，其系数应该显著，即MAXfactorIV会产生风险溢价。如果MAX的系数显著，同时MAXfactorIV载荷的系数不显著，这就意味着赌博型收益并非源于风险承担，而是源于赌博型股票的错误定价。

2SCSR的解释变量为MAX和四因子载荷，被解释变量为组合平均超额收益。表5的Panel A是控制住MAX影响而进行了10等分的组合回归结果;Panel B为同时控制了公司规模、账面市值比和MAX影响而形成的125个组合的回归结果。由表5可知，MAXfactorIV载荷对股票收益的影响远小于赌博特征， 因为在各种分组情况下，MAXfactorIV载荷拟合值的绝对值都远小于MAX的拟合值。MAX拟合值的t值较大，而且大于MAXfactorIV载荷拟合值的t值绝对值，这说明赌博因子载荷的收益解释能力被MAX所表征的赌博特征所覆盖， 而赌博特征的收益解释能力不能被赌博因子载荷所覆盖。据此可知，赌博型收益是由错误定价造成的，并非源于定价模型遗漏了相关风险因子。

五、稳健性检验

（一）四因子描述性统计分析

根据崔惠颖等（2016）的观点，特质偏度（IS）对股票赌博特征的识别能力仅次于MAX， 并与预期特质偏度（EIS）相关性很大[8]。为使赌博特征识别指标的选择不影响到前文的实证结果，本文计算了剔除EIS影响的赌博因子ISfactorEIS，具体计算过程同MAXfactorIV。

表6对ISfactorEIS与Fama-French三因子进行了初步的描述性统计， 并计算了四各因子的相关性。其中，ISfactorEIS对应的t值为3.77，通过显著性检验。另外，Fama-French三因子与ISfactorEIS没有表现出较高的相关性，这说明ISfactorEIS是有效的。

（二）全样本期的多因子模型检验

表7和表8是基于ISfactorEIS的全样本期三因子和四因子模型检验结果。分别按Size和IS进行五等分、BM和IS进行五等分的检验结果如表7、表8的Panel A和Panel B所示。 表中只展示了回归结果中的截距项、 拟合优度和ISfactorEIS拟合情况。

通过对比表7和表8的Panel A、Panel B可以发现与前述结论相同。 一是ISfactorEIS具有较好的收益解释力，这表现在赌博因子降低了截距项的显著性，提高了回归的拟合优度，而且绝大部分的ISfactorEIS系数显著。 二是ISfactorEIS的系数拟合值和t值也呈现出随IS的增大而由正变负的变动趋势， 表明ISfactorEIS对收益的解释力可能与MAXfactorIV一样，均受到赌博特征的影响。

（三）基于分组法的定价检验

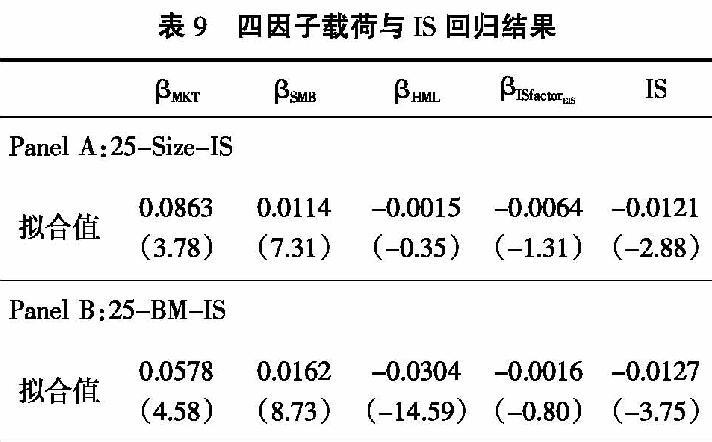
与MAXfactorIV相同， 表9列示了ISfactorEIS的分组法2SCSR定价检验， 以具体分析赌博因子ISfactorEIS的收益解释能力与赌博特征的关系。对比表9和表5，IS和ISfactorEIS的收益解释能力分别弱于MAX和MAXfactorIV。 不过一致之处在于，在Panel A和Panel B中，IS的回归系数绝对值及其t值绝对值分别大于ISfactorEIS载荷的回归系数绝对值及其t值绝对值。 这意味着，ISfactorEIS载荷的收益解释能力能被IS所表征的赌博特征控制，而IS赌博特征的收益解释能力无法被ISfactorEIS载荷控制。 可见，ISfactorEIS的检验结果同样支持了错误定价假说。

综上所述，本文的检验结果证实赌博型收益源于错误定价， 而非源于定价模型遗漏风险因子，不支持“风险承担”假说，而且结果不受赌博型股票识别指标和赌博因子选择的影响。

六、结论与启示

股市赌博行为表现在对收益正偏股票的追逐，而这类股票只能给投资者带来无法被经典定价模型所解释的负异常收益，即赌博型收益。由于投资者的赌博偏好无法直接观测，而赌博型收益正是投资者赌博偏好的市场表现。因此，对赌博型收益的成因研究， 将有助于对股市投资者赌博偏好的理解，进而更有针对性地防范化解股市风险。

理论上，赌博型收益可能源于投资者的风险偏好（风险承担解释），也可能源于投资者的有限理性（错误定价解释）。“风险承担解释”认为赌博型收益是由定价模型的误设而导致的，即定价模型遗漏了某一定价因子，它能够控制住赌博型股票的风险回报。“错误定价解释”则认为，赌博型收益是赌博型股票因投资者的有限理性而被错误定价。不同于以往的研究，本文综合地对赌博型收益成因的这两种解释进行了检验，系统地分析了赌博型收益究竟是由错误定价所导致的，还是一种风险承担的结果。

本文对赌博型收益成因的检验结合了多因子定价模型和两阶段横截面回归。首先，基于中国股市现实情况，计算了合适的赌博因子。其次，将三因子和四因子模型的拟合结果进行对比。通过多种分组方式， 控制赌博特征等因素对股票收益的影响，进而初步识别赌博风险定價和赌博特征定价。最后，进一步利用2SCSR方法加以确认。赌博指标和赌博因子载荷同时引入多因子定价模型，对比分析赌博特征与赌博因子的收益解释力。本文的实证结果发现：

第一， 本文构建的赌博因子MAXfactorIV和ISfactorEIS均通过了显著性检验，且与其他因子相关性低，说明它们是有效因子。第二，在多因子定价模型的检验中，通过比较加入赌博因子前后的赌博因子拟合值及其显著性、 截距项拟合值及其显著性，以及回归拟合优度等三个方面，发现如下规律：（1）赌博因子对股票收益具有解释能力，而且股票的赌博特征呈现非线性变化。（2） 赌博因子系数明显地随股票赌博特征的增强而由正变负。这说明赌博因子载荷与赌博特征有一定相关性，赌博特征可能是赌博因子的股票收益解释力的原因，或者赌博特征对股票收益的影响没有被赌博因子充分控制。

第二，通过2SCSR发现，股票赌博特征能够控制赌博因子载荷的收益解释能力，而赌博因子载荷无法控制赌博特征的收益解释能力。据此，本文认为赌博型收益不是源于赌博型股票承担了特殊的风险，而是由于被错误定价。也就是说，我国股市投资者的赌博偏好是一种有限理性的表现，并非出于风险承担。

在金融风险日益凸显的现实背景下，对赌博型收益的成因研究也提醒股市投资者应充分认识非理性因素在投资决策中所起到的重要作用。投资者要尽量克服“追涨杀跌”等心理因素和行为偏差所带来的不利影响。另外，根据行为金融学理论，错误定价能够长期存在，除了受到投资者的心理因素和行为偏差的影响之外，还受到套利限制的影响。因此，监管部门还需继续引入并完善卖空制度，维护一个良好的信息环境和交易环境。

参考文献：

[1]刘圣尧，李怡宗，杨云红.中国股市的崩盘系统性风险与投资者行为偏好[J].金融研究，2016（2）：55-70.

[2]KUMAR A.Who Gambles in the Stock Market？[J].Journal of Finance，2009，64（4）.

[3]BALI T G，CAKICI N，WHITELAW R F.Maxing out：Stocks as Lotteries and the Cross-section of Expected Returns[J].Journal of Financial Economics，2011，99（2）.

[4]WALKSH？魧USL C.The MAX Effect：European Evidence[J].Journal of Banking & Finance，2014，42（42）.

[5]郑振龙，孙清泉.彩票类股票交易行为分析：来自中国A股市场的证据[J].经济研究，2013（5）：128-140.

[6]江曙霞，陈青.赌博特征股票的收益预测及解释[J].财贸研究，2013（3）：99-107，116.

[7]李培馨，刘悦，王宝链.中国股票市场的赌博行为研究[J].财贸经济，2014（3）：68-79.

[8]崔惠颖，王志强.博彩型股票的识别分析——来自中国股票市场的经验证据[J].商业经济与管理，2016（5）：86-96.

[9]梁昱，张伟强.博彩型股票与投资者的博彩性偏好——基于中国股票市场数据的实证研究[J].运筹与管理，2017（2）：117-126.

[10]崔惠颖.博彩型收益的时变性分析——来自中国股票市场的经验证据[J].商业研究，2019（1）：24-31.

[11]崔惠颖.股市投资者赌博行为收益形成机理研究 ——基于情绪的错误定价分析[J].商业研究，2019（8）：63-72.

[12]BRUNNERMEIER M K，GOLLIER C，PARKER J A.Optimal Beliefs，Asset Prices，and the Preference for Skewed Returns[J].American Economic Review，2007，97（2）.

[13]BARBERIS N，HUANG M.Stocks as Lotteries：The Implications of Probability Weighting for Security Prices[J].American Economic Review，2008，98（5）.

[14]ZHONG A，GRAY P.The MAX Effect：An Exploration of Risk and Mispricing Explanations[J].Social Science Electronic Publishing，2016.

[15]崔惠颖.股市投资者赌博行为研究综述[J].金融理论与实践，2019（7）：77-83.

[16]陈文博，陈浪南，王升泉.投资者的博彩行为研究——基于盈亏状态和投资者情绪的视角[J].中国管理科学，2019（2）：19-30.

[17]徐小君.公司特质风险与股票收益——中国股市投机行为研究[J].经济管理，2010（12）：127-136.

[18]CORE J E，GUAY W R，VERDI R.Is Accruals Quality a Priced Risk Factor[J].Journal of Accounting and Economics，2007，46（1）.

[19]HIRSHLEIFER D，HOU K，TEOH S H.The Accrual Anomaly：Risk or Mispricing[J].Management Science，2012，58 （2）.

[20]HARVEY C R，AKHTAR S.Conditional Skewness in Asset Pricing Tests[J].Journal of Finance，2000，55（3）.

[21]KUMAR A，PAGE J K.Deviations From Norms and Informed Trading[J].Journal of Financial & Quantitative Analysis，2011，49（4）.

[22]FAMA E F，FRENCH K R.The Cross-Section of Expected Stock Returns[J].The Journal of Finance，1992，47（2）.

Research on the Return of Gambling Preference in Chinese Stock Market Based on Multi-factor Model

Cui Huiying

（School of Economics and Business Administration， Heilongjiang University， Harbin 150080， China）

Abstract：In recent years， the stock market has always been the main area of Chinese financial risks， and investor gambling preference is an important reason for stock market volatility. Based on multi-factor pricing model and two-stage cross-sectional regression， this paper examines the mechanism of the influence of “mispricing” and “risk taking” on gambling preference and its negative abnormal returns. We find that the gambling factor based on the maximum daily rate of return has explanatory power for return. And its regression coefficients obviously change from positive to negative with the increase of gambling characteristics. This means that gambling factor load is related to gambling characteristics. Further using two-stage cross-sectional regressions， we find that gambling characteristics can control the explanatory power of gambling factor loads， and lottery-like return is due to the mispricing of lottery-like stock rather than a certain risk-taking behavior. This means that the gambling preference of investors in Chinese stock market is a kind of bounded rationality rather than risk-taking.

Key words： gambling preference： lottery-like return; risk preference; bounded rationality

（責任编辑、校对：卢艳茹）