摩擦塞焊非稳态阶段温度场的数值模拟
2019-01-22
(南京航空航天大学,江苏南京210016)
0 前言
摩擦塞焊(friction plug welding)又称为摩擦塞补焊,是一种固相连接技术[1]。其基本原理是在待焊工件上钻出一定大小的锥形通孔,并制出与基体材料相同的对应的焊接棒,当摩擦塞焊的焊接棒以较高转速且在一定焊接速度下进入锥形通孔时,通过焊接棒与焊件之间的相互摩擦,使焊接棒和焊件连接,然后在一定的顶锻力作用下,使得连接处的材料组织晶粒更加细小,从而有效保证补焊接头处的质量。摩擦塞焊具有环保、焊接速度快、可在恶劣环境中焊接等优点,常用于航空、航天、航海等领域的装备修复和搅拌摩擦焊的“匙孔”修补。
摩擦焊接过程可分为非稳态、稳态、顶锻三个阶段。相对于其他阶段,非稳态阶段的焊接过程极其复杂,而其所占产热比例仅为10%[2],研究人员大多选择简单的库伦摩擦产热模型[3]或直接忽略来处理该阶段的产热。因此,相对于其他阶段来说,对于这一阶段的认识和理解还有待提高。
同时近年来,一些无顶锻特殊摩擦焊工艺表明,在一些特殊的情况下焊接接头成形无需经历稳态和顶锻阶段,这说明非稳态阶段的摩擦产热过程也同样重要[4]。
本研究基于摩擦塞焊非稳态阶段产热功率线性增长规律[5],建立相应的产热模型,利用非线性有限元软件ABAQUS建立7075-T6铝合金摩擦塞焊非稳态阶段的热力耦合三维模型,预测温度场及应力场分布,并验证模型的正确性。
1 非稳态阶段产热模型
1.1 状态转变判据
当非稳态阶段进入稳态阶段时,界面材料发生完全塑性流动,此时摩擦界面的产热机制由滑动摩擦产热完全进入金属塑性流动的粘性产热机制。根据金属塑性成形原理中关于材料发生塑性变形的相关知识可知,当σe≥σs(T)时,即材料所受等效应力超过其屈服极限后才会发生塑性变形,σe为等效应力,σs(T)为温度T时材料的屈服强度。在摩擦塞焊中,设圆台体塞棒锥角为2β,根部和端部半径分别为R1和R2,摩擦界面材料受到压力、扭矩复合作用,如图1所示,材料所受等效应力为

式中 τ为摩擦剪应力;P为界面材料所受压力。

图1 摩擦塞焊接过程中界面金属受力分析
在材料未发生屈服时,界面主要以滑动摩擦擦热为主,则摩擦剪应力为

可得

在铝合金摩擦塞焊峰值时刻的材料发生黏着摩擦,摩擦系数为0.8。由文献[6]查得7075-T6铝合金随温度变化的屈服强度如图2所示,进一步拟合得到其屈服强度与温度(T>273 K)之间的关系式为

联立式(1)~式(4)可求得发生产热机制转变时的临界温度,即焊接接头温度场的最高温度Tmax,它既是非稳态阶段接头温度场的右极限,又是准稳态阶段接头温度场的左极限。
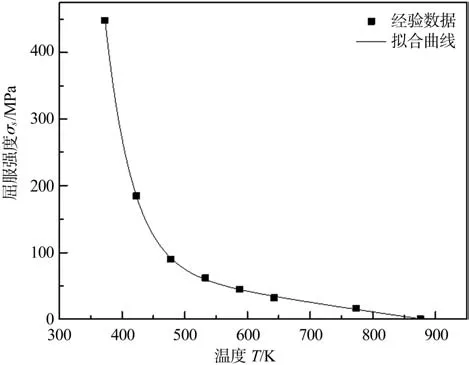
图2 7075-T6铝合金屈服强度随温度的变化曲线[6]
1.2 峰值产热功率的解析
由于产热的连续性,非稳态阶段产热功率的右极限也是稳态阶段产热功率的左极限,同时在稳态阶段产热功率近似不变,因此峰值时刻的产热功率即为稳态阶段的塑性变形产热功率。
峰值时刻产热功率的解析基于以下假设条件:
(1)焊接件为薄板且塞孔倾角较小,这些减少了温度、应力以及应变等梯度在高度方向的差异,因此可视温度、应力应变场、塑性区厚度在高度方向上是不变的,同时认为焊接过程中的压力、转速是恒定的。
(2)稳态阶段下,板件上任一点的温度、应力应变以及流动速度仅与其距塞孔中心的距离有关。
(3)摩擦界面两侧材料的温度、应力应变、流动速度场对称。
(4)将稳态阶段的粘塑性金属流动视为非牛顿、不可压缩的层流。
(5)焊接板件可以被分为塑性区和弹性区两部分,如图3所示。
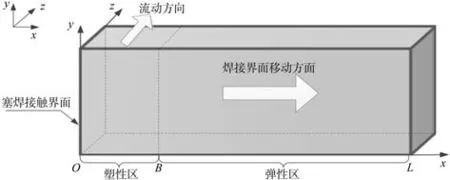
图3 材料流动示意
基于以上假设,摩擦塞焊稳态阶段问题可简化为1D模型问题。在如图3中所示的直角坐标系中,接触界面、塑性区与弹性区界面以及板件端面分别位于x=0、x=B、x=L处。同时稳态阶段的温度、塑性 流动速度变化曲线如图4所示。

图4 温度、流动速度曲线示意
由质量守恒和动量守恒推导不可压缩单相流体的控制方程为[7]

在摩擦塞焊焊接过程中,ν远小于塞棒的线速度,因此式(6)中的 ν、ux和 uy可忽略不计[8],简化可得

式中 u为图4b或式(6)中的uz;μ为粘度,与流体应力和等效应变有关,关系式为

式中 σe为流体应力;ε为等效应变速率[9]。

将式(8)、式(9)代入式(7)中积分求解,并结合边界条件 x=B 处 σe=τ(TB)可得

虽然塑性层温度梯度较大,但考虑到其厚度一般约为1 mm,温度相差较小,不超过几十摄氏度,可认为TB=Tmax-20[9-10]。
进入到稳态阶段,塑性区的粘塑形流体金属处于高温、高应变速率状态。Sheppard、Wright[11]提出了针对铝合金材料的粘塑性流体应力的本构方程,其表达式为

式中 A、α和n均为与材料相关的参数;Z为Zener-Hollomon参数

式中 G为通用气体常数;ΔH为变形激活能;T为绝对温度。
联立式(10)、式(12)可得

为求出流动速度u,Aukrust[12]提出了一种简化方案:当 x>>1 时,sinh-1x≈ln 2x。在铝合金摩擦焊中一般满足此要求[9-10]。将式(13)简化为

在塑性流动区温度梯度较小,同时塑性流动区宽度一般约为1 mm,结合温度变化曲线(见图4a)可知,在塑性流动区的温度差较小。因此,可用塑性流动区的平均温度代替式(14)中的T,联立式(13)和式(14),积分求解并考虑边界条件 x=0,u=0(见图 4b)可得
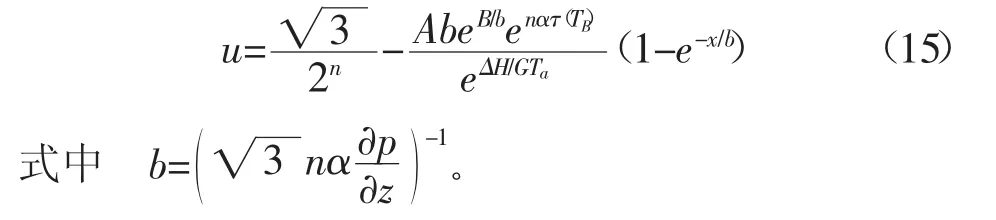
联立式(9)、式(15)可得应变速率为
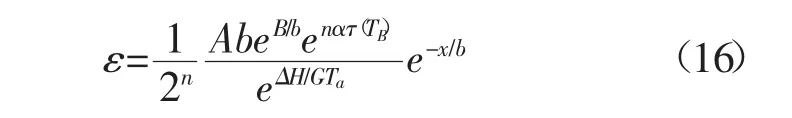
由式(18)可知,当x由0逐渐增至b时,ε急剧减少,但当x由b逐渐增至B时,ε缓慢减少。因此可将塑性流动区与弹性区的界面定义在x=b处,即塑性流动区的厚度B为

Xiong等[9]通过对粘塑性金属的流动速度进行线性化处理得到界面应变速率表达式为

式中 vl为线速度的50%。

式中 ω为塞棒角速度。
结合式(11)、式(12)可得

则体积为V的材料塑性变形产生的热量为

式中 η为塑性变形能转化为热能的效率。
摩擦塞焊塑性变形产热可分为塞棒塑性变形区产热PB1(B1为该塑性区厚度)和基材塑性变形区产热PB2(B2为该塑性区厚度)。由于塞棒与基材为同种材料,塞孔半径一般大于5 mm,因此可近似认为B1=B2=B。取η=1,则摩擦塞焊稳态阶段塑性变形产热功率Pw为

由假设(3)可知,材料应力应变关于界面对称,以塞棒中心为原点,板件长度方向为x轴,结合式(18)、式(20)和式(21),可得塞棒塑性变形区产热PB1为

基材塑性变形区产热PB2为

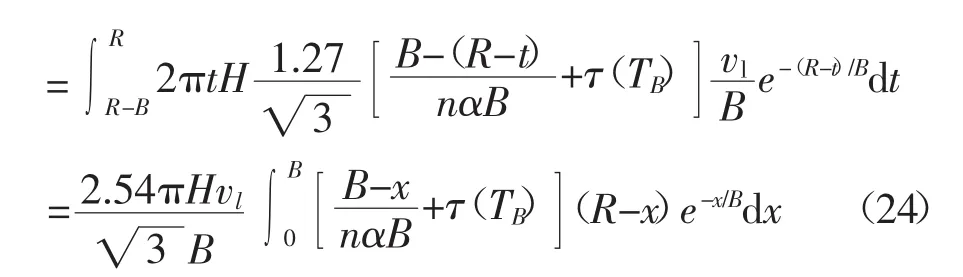
可得稳态阶段塑性产热功率为

式中 R=(R1+R2)/2。
峰值时刻的热流密度为

式中 S为摩擦界面的面积。
2 非稳态阶段有限元模型
2.1 几何模型及网格划分
焊接材料为7075-T6铝合金,尺寸为60 mm×60 mm×2 mm,塞孔小径为 10 mm,倾角 β=20°。
基于非线性有限元软件ABAQUS建立了摩擦塞焊非稳态热力耦合三维有限元分析模型。模型选择通用分析步中的温度-位移耦合(Coupled tempdisplacement)对非稳态阶段进行分析,选择同时具有温度和位移自由度的C3D8RT单元,采用结构化网格划分技术,将靠近焊接区域的网格划分细致(1 mm)以提高计算精度,远离焊接区域的网格划分相对稀疏(2 mm)以减少计算量。最终网格模型如图5所示。

图5 几何模型及网格划分
2.2 边界条件
焊接开始前,工件温度等于室温(23℃),垫板和焊接铝板暴露在空气中的表面,空气的对流散热系数大小为0.03 mW·mm-2·K-1,焊接铝板和垫板之间的接触热传导系数为0.1 mW·mm-2·K-1,辐射散热则忽略不计[3]。
2.3 热源的加载
对于摩擦塞焊的热源模型,热输入区域为塞棒和焊接铝板的接触面,通过ABAQUS中的热流密度和压强载荷方式加载。其中焊接转速为3 500 r/min,焊接压力16 MPa,热流密度由式(26)确定。
3 数值模拟结果与讨论
3.1 摩擦塞焊焊接区域的温度场
热力耦合有限元模型模拟所得温度场和应力场分布如图6所示。可以看出,靠近焊接区域的表面温度场、应力场呈圆形分布,同时在板件厚度方向上不同位置的温度、应力基本仅与其距塞孔中心的距离有关,即任一点的温度、应力仅与其距塞孔中心的距离有关;温度大小在距焊接区域较远的位置变化很小,但应力变化则较为明显,同时由于受板件形状、尺寸的约束,较远处区域的应力场呈非规则圆形分布。
3.2 模拟结果与试验结果的对比
在焊接转速3 500 r/min、焊接压力16 MPa的工艺参数下,用热电偶及无纸记录仪测量板厚中间平面上距摩擦界面1 mm处的特征点在非稳态阶段的温度变化。试验结果特征点温度变化与数值模拟相应点温度变化的关系如图7所示。

图6 7075-T6铝合金摩擦塞焊非稳态温度场和应力场分布
由图7可知,虽然非稳态阶段初期的数值模拟结果高于试验测量结果,而到后期其又低于试验测量结果,但是数值模拟结果变化趋势与试验测量结果在整体上基本一致。这是因为产热功率只是简单地在整个非稳态阶段进行线性化,同时在非稳态初期塞棒与塞棒的实际接触面积小于名义面积,导致此时产热效率偏低。总体来看,基于产热规律的线性化,建立的热力耦合三维有限元模型对摩擦塞焊非稳态阶段的数值模拟是可行的。
4 结论
(1)基于摩擦塞焊非稳态阶段的产热线性规律,利用有限元分析软件ABAQUS建立了摩擦塞焊非稳态阶段热力耦合三维有限元模型。
(2)数值模拟实现了对摩擦塞焊 非稳态阶段焊接温度场及应力场分布的预测,进一步将模拟结果与试验测量结果进行比较,验证了产热模型及有限元模型的正确性。
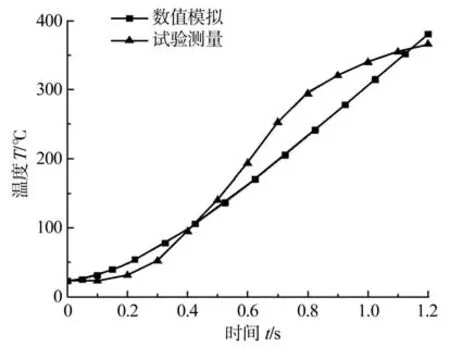
图7 测温特征点温度模拟结果和试验结果比较
(3)通过分析数值模拟的温度场及应力场结果,发现在靠近焊接区域的任一点的温度及应力仅与其距塞孔中心的距离有关,这也说明了假设的正确性。
