一种改进的模糊二元对比决策新方法*
2019-01-22马锦锦
马锦锦
(安徽建筑大学数理学院 安徽合肥 230601)
经典的模糊二元对比决策方法在比较过程中丧失了大量对比信息,因此,需要提出一种改进的模糊二元对比决策新方法,使得在计算过程中能够避免二元对比信息的缺失,从而避免出现排序结果的不准确,甚至与实际情况完全不符的情况出现[1-2]
文中主要用到的量有:
n:备选方案(对象)数量
论域U={x1,x2,…,xn}:n个备选方案(对象)
xi:对比的量
A:模糊集
λ:所取阈值
优先选择比rij:ri与rj相比较时ri对于A比rj对于A优越的程度
R=(rij)n×n:由rij组成的n×n阶矩阵
fj(xi):xi与xj的比较中,xi具有某种特性的程度
(fj(xi),fi(xj):xi与xj对该特性的二元相对比较级
Φ:二元相对比较矩阵f(xi|xj):模糊相对比较函数
1 改进原因
引例:对于一个模糊集U={a1,a2,a3,a4},它的模糊优先关系为:

由模糊优先关系排序决策,先选出每行的下确界,得到最优为a3,划去a3所在行与列,重复上述步骤,可以得到优劣次序为a1,a2,a3,a4.但是,能看到r14=0.5,即a1与a4的优先度相同;r43=0.6,即a4的优先度高于a3;r21=0.1,r24=0.65即a2的优先度远低于a1,但是却仅大于a4.可以看出,利用模糊优先关系排序决策确定的事物优劣次序是不合理的,在有些情况下甚至无法接受.通过观察模糊优先关系排序决策的具体步骤时,可以看出,当确定第k+1名对象时,由于该对象所在的行与列已经删去,剩下的(n-k)个待排序的对象与前k名对象的二元对比信息已经失去,因此,在的计算中可能会得到比较大的误差,甚至会得到完全相反的结论[2-3].
因此,需要提出一种改进的模糊二元对比决策的方法,使得在计算过程中能够避免二元对比信息的缺失,从而避免出现排序结果的不准确,甚至与实际情况完全不符的情况出现.
2 改进的模糊二元相对优先关系排序方法
针对上述所出现的问题,文章提出一种改进的方法,使得在进行模糊二元对比的过程中,不会造成二元对比信息的缺失.
具体步骤如下:
(1)论域U={x1,x2,…,xn}上的模糊优先关系为B,优先选择比bij满足如下条件:
(1)
以上条件表明,xi与xi相比较时,没有优越性,记为bii=0;xi与xj相比较时总是各有所长,把两者的优越成分合在一起就是1,即bij+bji=1 ;当只发现xi比xj有长处而未发现xj比xi有任何长处时,记bij=1,bji=0;当xi与xj相比较时优先度一样,记bij=bji=0.5.
满足式(1)的bij组成的矩阵B=(bij)n×n为模糊优先关系矩阵.
此步骤的具体方法与原有的构建模糊优先关系矩阵的方法一样,无需做任何改动.
(2)在引例中,原有的方法的缺点在于在进行二元对比的过程中,丧失了二元对比信息,因此在本节改进方法中,应该做到充分利用每个二元对比的信息.
在构建模糊二元相对优先关系矩阵时,可以利用xi与xj相比较时的优先度bij与其他对象相对xj的优先度进行对比,再将对比的结果结合到一起,构成此矩阵中的每一个数据.
首先,计算出(bij-b1j)2,(bij-b2j2),……,(bij-b(i-1)j)2,(bij-b(i+1)j)2,(bij-b(nj))2,再将这些结果相加,但是,由于bij-b1j,bij-b2j,……,bij-b(i-1)j,bij-b(i+1)j,bij-bnj的结果可能为正也可能为负,避免结果出现不准确的情况,需要定义一个k,若这些式子的结果为正,则令k=1,将 与对应的式子相乘;相反,若这些式子的结果为负,则令k=-1,即计算:
k1(bij-b1j)2+k2(bij-b2j)2+…+ki-1(bij-b(i-1)j)2+ki+1(bij-b(i+1)j)2+kn(bij-bnj)2
(2)

综上,定义一个fi(xj),令
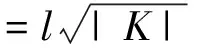
(3)
其中,
K=k1(bij-b1j)2+k2(bij-b2j)2+…+ki-1(bij-b(i-1)j)2+ki+1(bij-b(i+1)j)2+…kn(bij-bnj)2

称fi(xj)为xi对于xj的优先度相对于其他对象优先的程度.fi(xj)是用来表示xi对xj的优先度bij相对于其他n-2个对象的优先程度.
(3)利用上一步中定义fi(xj),构建一个模糊矩阵W:
(4)
称矩阵W为模糊二元相对优先关系矩阵.
(4)将每一行的数全部相加,得到权重:
Wi=fi(x1)+fi(x2)+…+fi(xn)
(5)
比较Wi大小,按照从到大小的顺序排序,即为所要求的优先排序关系.
此步骤中,将各行的值相加,是为了比较出每个对象相对于其他对象的整体优先程度,然后进行比较,避免了本章开头遇到的对比过程中信息缺失的情况,充分利用了每一个二元对比信息.
3 改进方法的实例计算
用改进的方法验证引例,模糊优先关系矩阵为:

由公式(2)得:
=0.5590
=0.7616
=0.4387
=-0.2693
=0.2645
f4(x2)=
=0.5657
构建模糊矩阵(4),可以得到:
W=

计算出各权值为:W1=0.0472,W2=-0.9147,W3=0.9310,W4=0.1196比较大小,可得到优劣次序为a3,a4,a1,a2。相比于原来的方法,可以明显看出,此方法更加适用于实际情况,在比较的过程中,没有舍弃其他对象,精确度较高.
4 改进方法的优点
改进方法与原方法相比,其优点在于充分考虑实际情况,在进行二元对比的时候,构建了一个更为合理的矩阵.充分结合每个优先度进行比较,避免了原有方法中二元对比的信息缺失,在实际应用中可有效避免出现不完全正确甚至完全相反的结论,从而保证了排序结果的正确性和合理性[2-4],因此该方法更加适用于实际情况.
