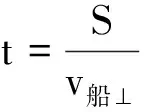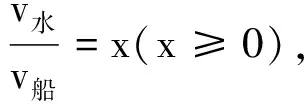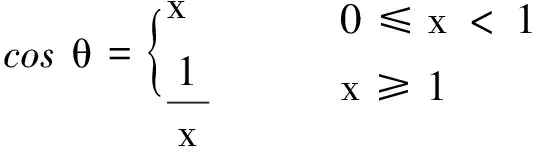对小船渡河最小位移问题进行定性和定量分析
2019-01-22姜璐涵
姜璐涵 周 航
[江苏省苏州中学高三(4)班 江苏 苏州 215007] (苏州大学物理科学与技术学院 江苏 苏州 215006)
小船渡河问题是高中物理中较为经典的题型,其本质上考察的是“矢量的合成与分解”这一知识点.针对小船渡河问题最常见的考点即为最小运动时间和最小运动位移的计算.其中,最小运动时间是比较容易理解和计算的,不论船速和水速的大小如何,只要使得船头的方向与河岸垂直,此时运动的时间即为最小.但对于最小运动位移的问题,则需要根据船速和水速的大小,不断调整船头的方向才能实现.
题目:有一条小河宽度为S,小船在静水中运动的速度为v水,河水流动速度为v船,求小船如何渡河才能使船行驶的位移最小?(假设水流动速度处处相等)
1 定性分析
(1)当v船>v水时
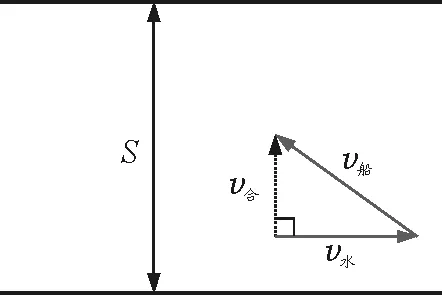
图1 v船>v水时v合与河岸垂直
如图1所示,可以通过调节船头的方向,恰巧使得合速度的方向与河岸垂直,此时小船运动到河对岸的位移最小,即为河宽S.
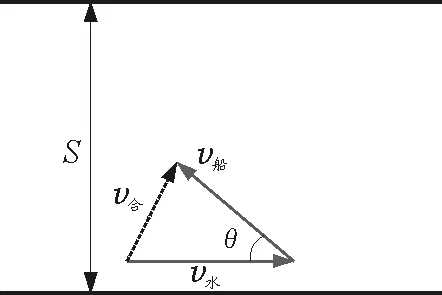
(2)当v船 图2 v船 v船,v水及v合3个矢量恰好构成了一个三角形,假设v船与v水的夹角为θ,如图3所示,根据余弦定理可得 (1) 把小船的速度v船分解为沿着河岸方向的v船‖和垂直于河岸方向的v船⊥两个分速度,则有 v船⊥=v船sinθ (2) 图3 v船与v水的夹角为θ 因为小船沿着河岸的分速度和水速均与河岸平行,故小船运动到河对岸的有效速度为v船⊥,则小船渡河过程中的有效时间为 (3) 小船渡河运动的位移为 L=v合t (4) 由式(1)~(4)得 (5) (6) 由小船渡河问题进行定性分析时知,只有调整船头的方向满足一定条件才能使得小船运动的位移最小,所以需要将L对θ进行求导,经计算和化简得 (7) 令式(7)=0,得 (8) 因为|cosθ|≤1,所以有 (9) 将式(9)代入式(6)得 本文通过定性分析和定量分析两种方法对小船渡河的最小位移问题进行了深入剖析.通过定性分析,对运动过程中的整个物理机制和原理有了更深层次的认识和理解;利用数学求导的思想进行定量分析,使解题思路更加清晰明了,在一定程度上提高了跨学科素养和综合解决问题的能力. 高中物理知识与生活密切相关,因此生活中的物理现场也常被搬到物理课堂中.但往往会出现很多物理问题需要以数学知识为抓手,这就使得我们很难进行定量分析.所以,高中学生可以尝试或者思考如何将数学知识或方法融合到物理思维当中.这不仅可以使得相关物理问题迎刃而解,也能实现从点到线再到面的全方位提高学生的综合素质.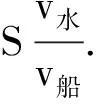
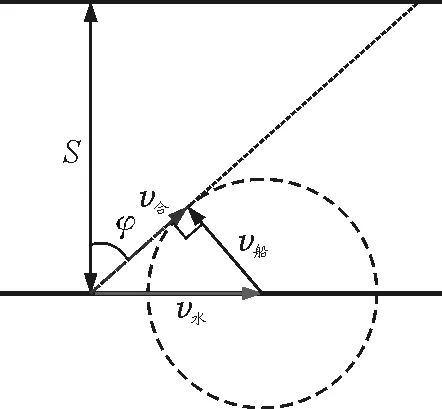
2 定量分析