基于常规电测井资料的各向异性储层水平井测井解释
2019-01-19徐波汪忠浩伍东
徐波,汪忠浩,伍东
(1.长江大学工程技术学院,湖北荆州434020;2.长江大学武汉校区,湖北武汉430100;3.中国石油长城钻探工程公司,北京100020)
0 引 言
国内外各向异性储层水平井测井研究主要集中在新型电阻率测井仪器及资料,如阵列感应测井[1-3]、三分量感应测井[4-8]、随钻电阻率测井[9-10]、随钻方位电阻率测井[11-18]等。而常规电测井在水平井中应用仍十分广泛。由于水平井与直井测量环境的差异,导致水平井中电测井资料受储层各向异性影响而无法直接用于储层测井评价。因此,针对常规电测井资料开展各向异性研究具有重要的理论和实际意义。
基于水平样和垂直样岩电参数,分析了ZY区块的各向异性变化规律。基于Klein模型[19-20],提出了“双岩电参数法”水平井电阻率各向异性测井评价方法。在此基础上,不考虑泥岩各向异性,分别对不同相对角、不同泥岩电阻率和不同砂岩电阻率情况下,模拟计算并分析了测量视电阻率随泥质体积含量的变化情况。最后利用Archie公式[21]处理实际井资料,取得了较好的效果,为水平井常规电测井资料各向异性评价提供了参考。
1 ZY区块岩电参数各向异性特征
ZY区块设计岩电实验方案为2个方向即水平和垂直方向上取心并测定岩电参数。水平样取心:ZY区块的HH74井C8段(深度段2 337~2 352 m)9块样品、HH73井C8段(深度段2 266~2 302 m)4块样品、HH62井C8段(深度段2 259~2 263 m)2块样品,共15块。垂直样取心:ZY区块的HH74井C8段的5块样品、HH73井C8段的7块样品、HH62井C8段的5块样品,共17块。
分析ZY区块岩电资料得到水平样岩电参数为a=1.966 4,b=1.067 4,m=1.525 6,n=2.133 8(见图1),垂直样岩电参数为a=1.271 6,b=1.087 6,m=1.898 7,n=1.931(见图2)。岩电参数统计见表1。
在岩电实验数据分析结果基础上,对孔隙度分别为0.06、0.08、0.1、0.15和0.2,含水饱和度从0.3~0.8时,模拟计算其各向异性系数λ(见图3)。

图1 ZY区块水平岩样岩电实验分析图版
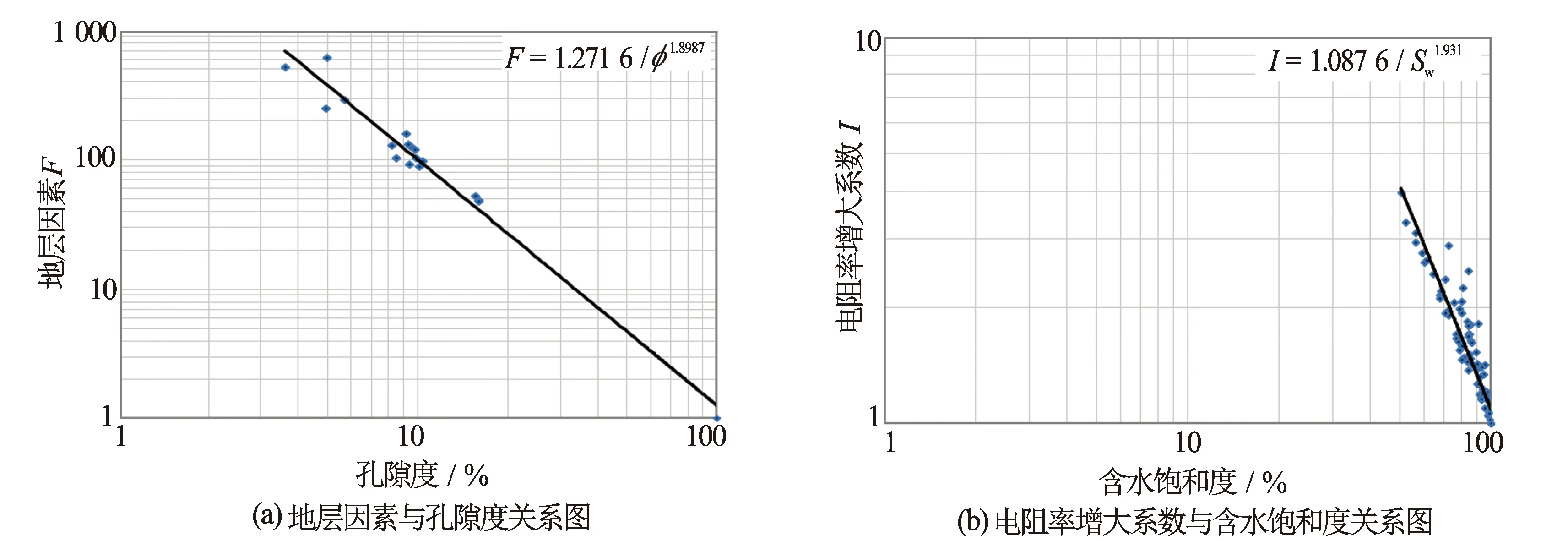
图2 ZY区块垂直岩样岩电实验分析图版
计算结果表明,各向异性系数随含水饱和度增大而增大,随孔隙度减小而增大。当孔隙度在0.06~0.1时,各向异性系数为1.1~1.3,储层表现出一定的各向异性特征。
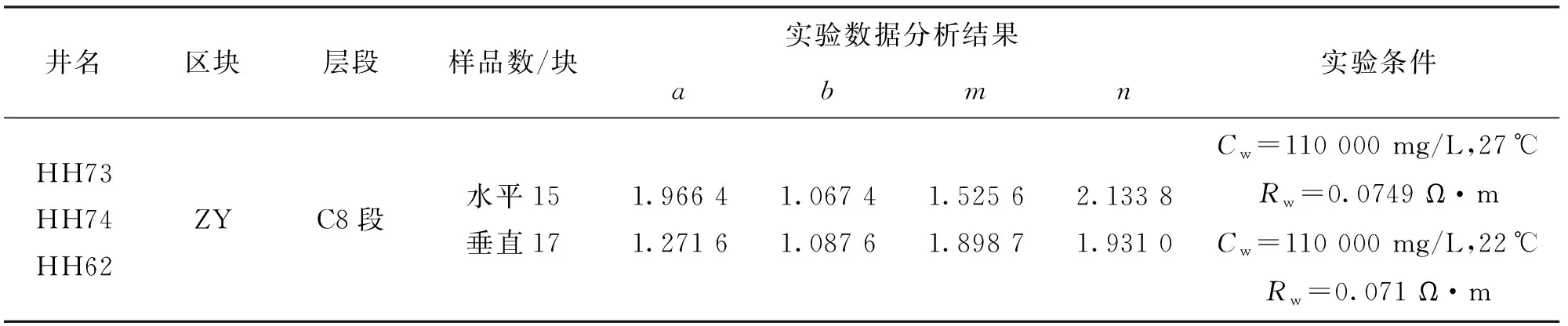
表1 岩电实验结果统计表

图3 ZY区块各向异性实验模拟计算
2 双岩电参数法水平井各向异性测井评价
基于各向异性理论,结合研究工区水平井测井资料特点,提出了双岩电参数法对水平井各向异性地层进行电阻率和饱和度的处理解释,该方法有一定的理论和实际应用价值。
2.1 “双岩电参数”各向异性计算方法
基于Klein模型[19],对视电阻率进行处理。该方法计算各向异性系数为储层总的各向异性系数,即宏观各向异性和微观各向异性综合。处理流程图见图4,具体计算方法如下。
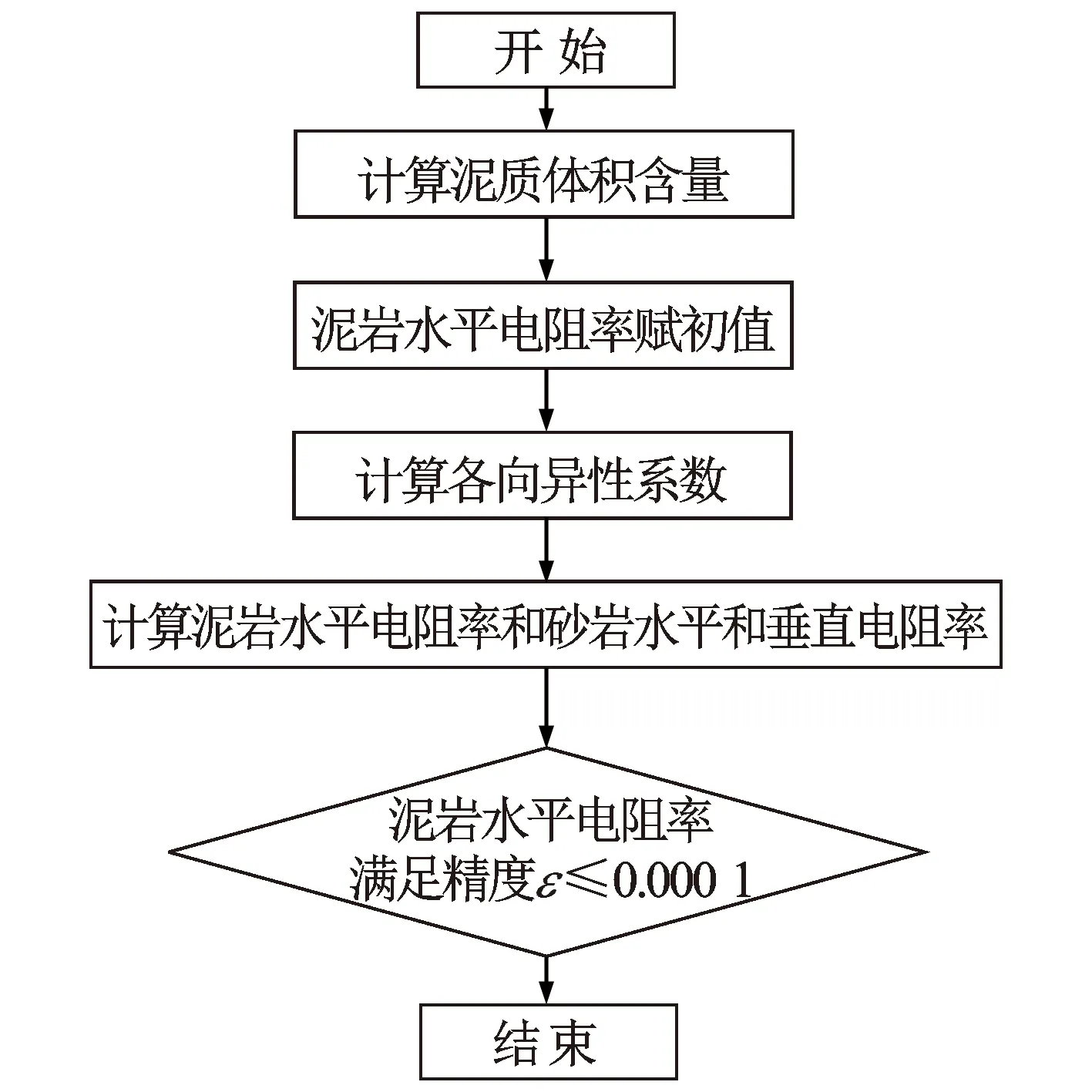
图4 感应测井各向异性计算流程图
(1)利用自然伽马曲线计算泥质体积含量Vsh和砂岩体积含量Vss。
(1)
(2)
Vss=1-Vsh
(3)
式中,GRss为自然伽马最小值(即纯砂岩自然伽马值);GRsh为自然伽马最大值(即纯泥岩自然伽马值);GR为自然伽马测井值,API;GCUR为希尔奇指数,研究区块该参数取3.7。
(2)计算地层总各向异性系数。
(4)
式中,Vss为砂岩体积含量,且Vss=1-Vsh;Vsh为泥质体积含量;Rss为各向同性纯砂岩电阻率值,Ω·m;Rshh0为初始泥岩水平电阻率值,Ω·m。
(3)计算水平电阻率Rh和垂直电阻率Rv。
(5)
Rv=λ2Rh
(6)
式中,Ra为感应测井仪测量深感应视电阻率,Ω·m;λ为地层总的各向异性系数,无量纲;α为井斜角。相对角σ=井斜角α-地层倾角。
(4)计算泥岩水平电阻率Rshh。
(7)
式中,Vss为砂岩体积含量;Vsh为泥质体积含量;Rh为计算水平电阻率,Ω·m;Rss为各向同性纯砂岩电阻率值,Ω·m。
(5)对比Rshh与Rshh0,若两者差值满足精度要求,则计算结束,否则返回第2步。将第4步计算的Rshh代入式(4),即令Rshh0=Rshh,循环迭代,直到满足精度要求,即|Rshh-Rshh0|<ε时停止迭代,ε为指定精度(通常取ε=0.000 1)。
通过上述步骤计算得到水平电阻率Rh、垂直电阻率Rv和各向异性系数λ。结合水平岩电参数和垂直岩电参数(即双岩电),利用Archie公式[21]计算相应的水平电阻率饱和度和垂直电阻率饱和度,计算公式
(8)
式中,a为岩性系数;m为胶结指数;b为流体系数;n为饱和度指数;Rw为地层水电阻率,Ω·m;φ为孔隙度,小数;Rt为地层电阻率,Ω·m。对于水平电阻率,Rt取Rh,选择水平岩样岩电参数;对于垂直电阻率,Rt取Rv,选择垂直岩样岩电参数。
2.2 各向异性影响分析
不考虑泥岩各向异性,分别对不同相对角、不同泥岩电阻率和不同砂岩电阻率情况下,模拟计算并分析测量视电阻率随泥质体积含量的变化情况。分析时不考虑地层倾角(即地层倾角为0),此时用相对角来表征井眼与地层的关系,即井眼与地层法线的夹角。
分析视电阻率(Ra)随泥质体积含量(Vsh)的变化情况(见图5)。当相对角从0°~90°变化时,视电阻率(Ra)随泥质体积含量(Vsh)增加而降低,泥质体积含量相同时,视电阻率随相对角增大而增大。
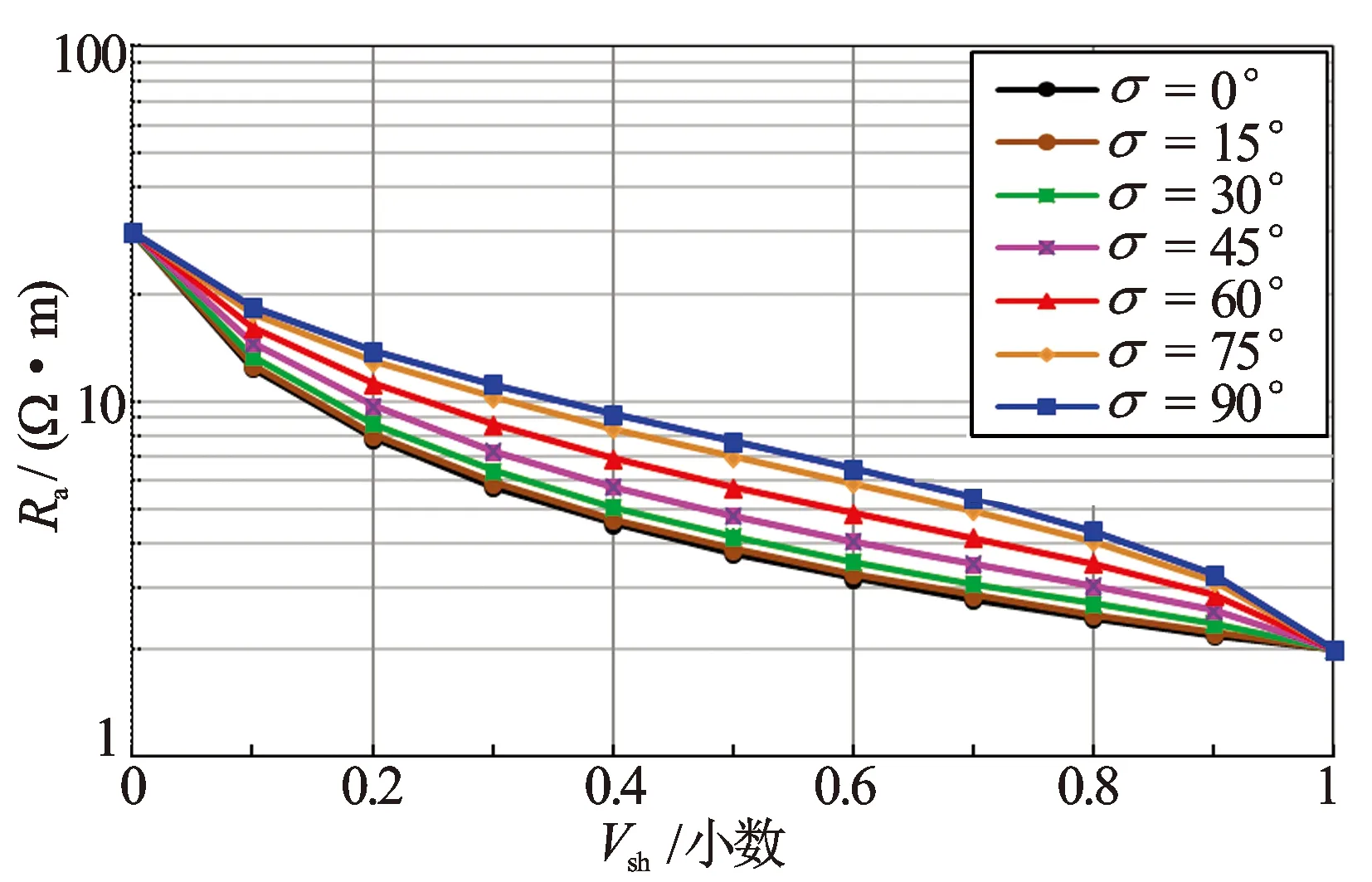
图5 视电阻率随相对角和泥质体积含量的变化规律
分析在相对角(σ)为90°时(即水平井)测量视电阻率(Ra)随泥质体积含量(Vsh)的变化情况。泥岩电阻率从1~5 Ω·m(见图6)。当泥质体积含量相同时,视电阻率(Ra)随泥岩水平电阻率(Rshh)增大而增大。
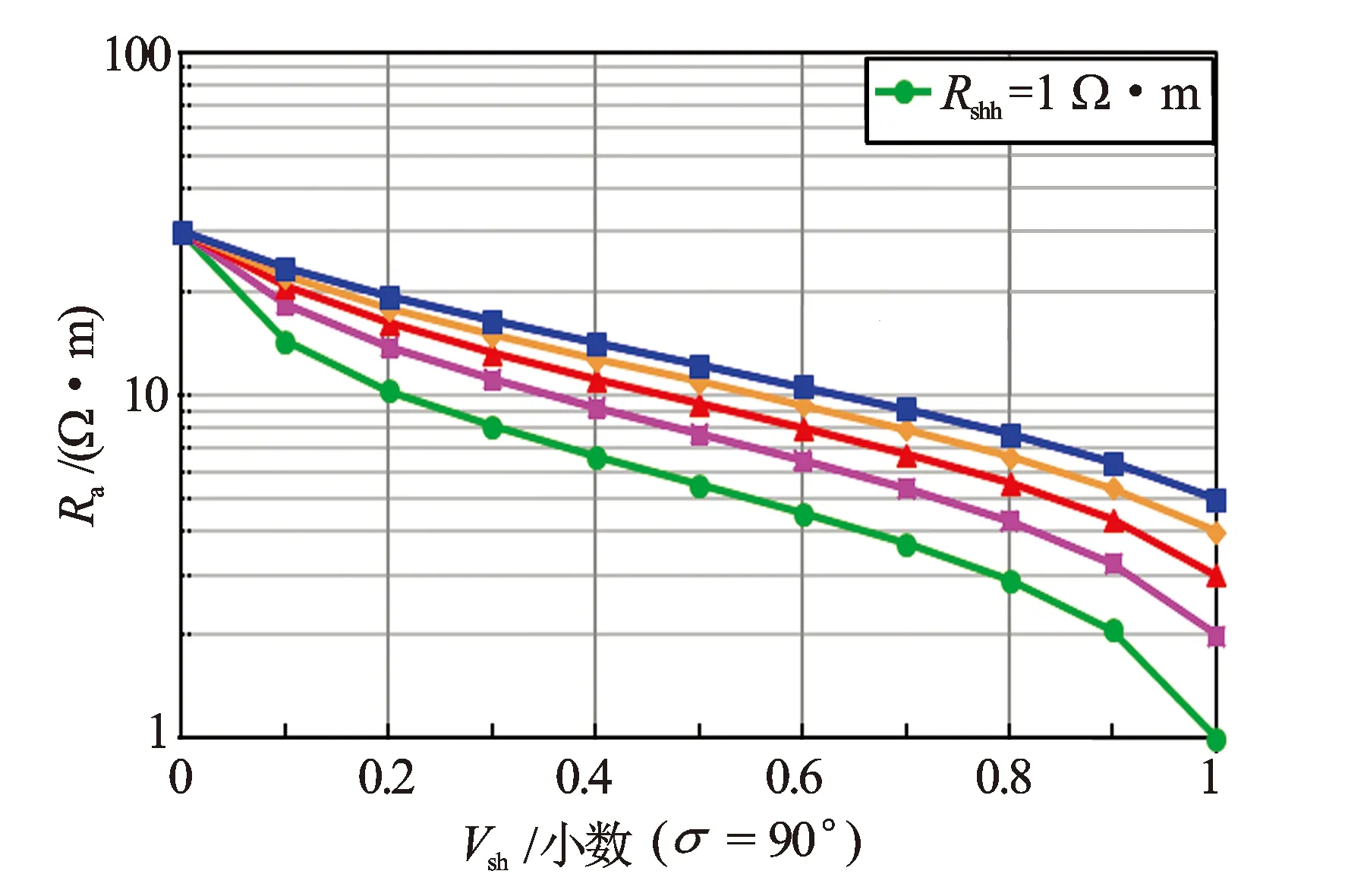
图6 视电阻率随泥岩电阻率和泥质体积含量的变化规律
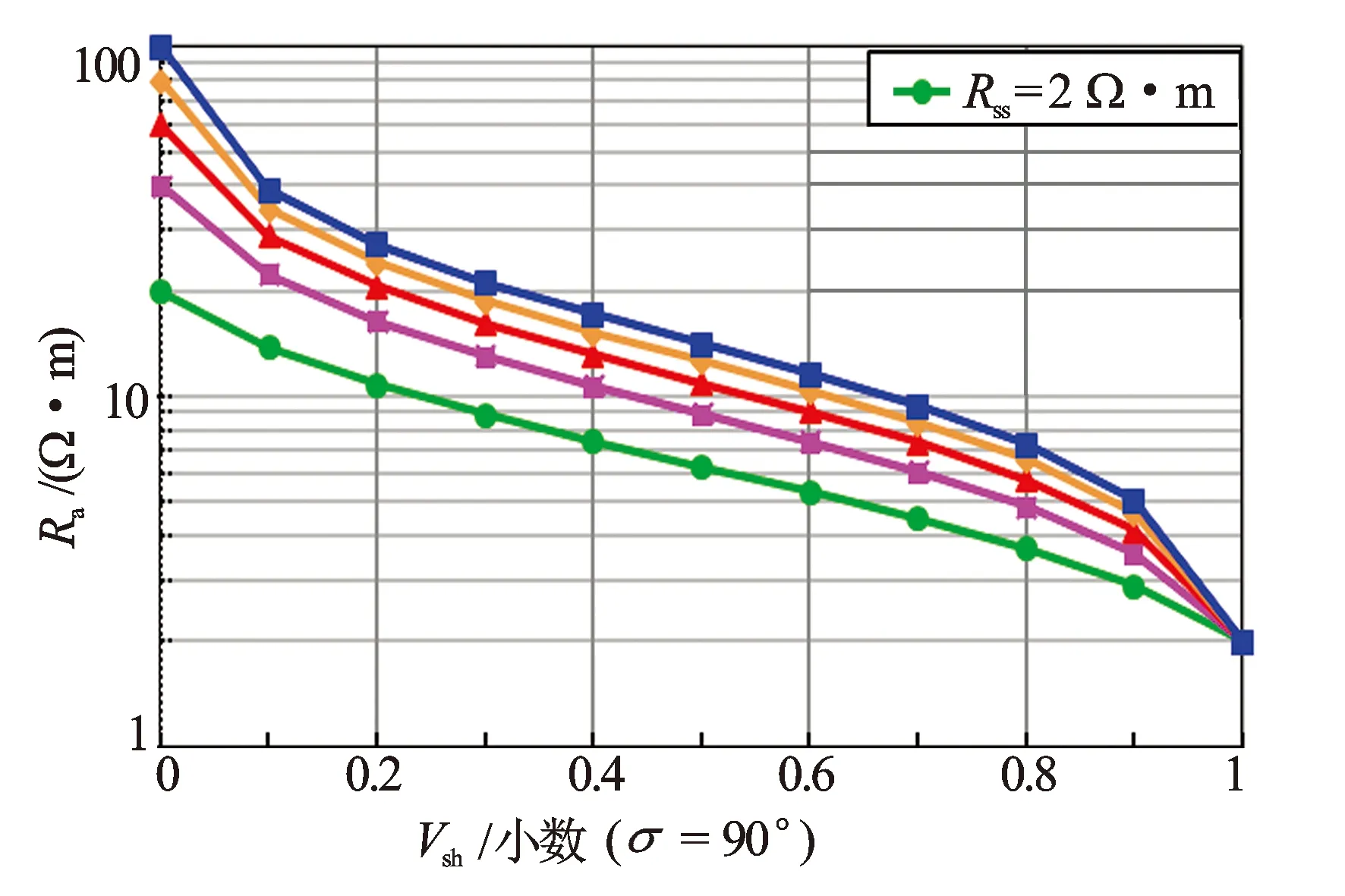
图7 视电阻率随各向同性纯砂岩电阻率和泥质体积含量的变化规律
分析相对角(σ)为90°时(即水平井)测量视电阻率(Ra)随泥质体积含量(Vsh)的变化情况。砂岩电阻率从20~100 Ω·m(见图7)。当泥质体积含量相同时,视电阻率随各向同性纯砂岩电阻率的增大而增大。
通过模拟计算,分别得到了视电阻率受相对角、泥岩电阻率、砂岩电阻率和泥质含量影响变化规律,为水平井各向异性储层测井评价提供了理论依据。
2.3 应用实例
利用双岩电参数法处理ZY区块3口井,利用各向异性计算得到的水平电阻率和垂直电阻率,分别计算对应水平电阻率含油饱和度SOH和垂直电阻率含油饱和度SOV,并与视电阻率计算含油饱和度SOA进行对比(见图8)。图9为HH74P1部分井段测井解释处理成果。
由处理成果图可知,计算的SOH与SOV比较接近,SOA与两者存在差异。利用“双岩电参数法”计算的饱和度(即水平电阻率计算饱和度SOH和垂直电阻率计算饱和度SOV)与邻近直井对应层段饱和度相当(约41%)。受各向异性影响,视电阻率计算饱和度SOA偏大。该方法计算结果与各向异性实验模拟计算结果是一致的(见图10),且与2.2节各向异性影响分析一致。
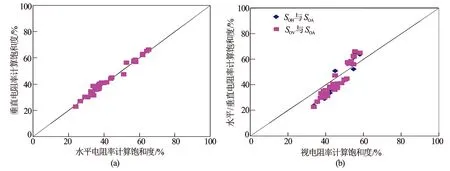
图8 ZY区块部分井计算饱和度对比
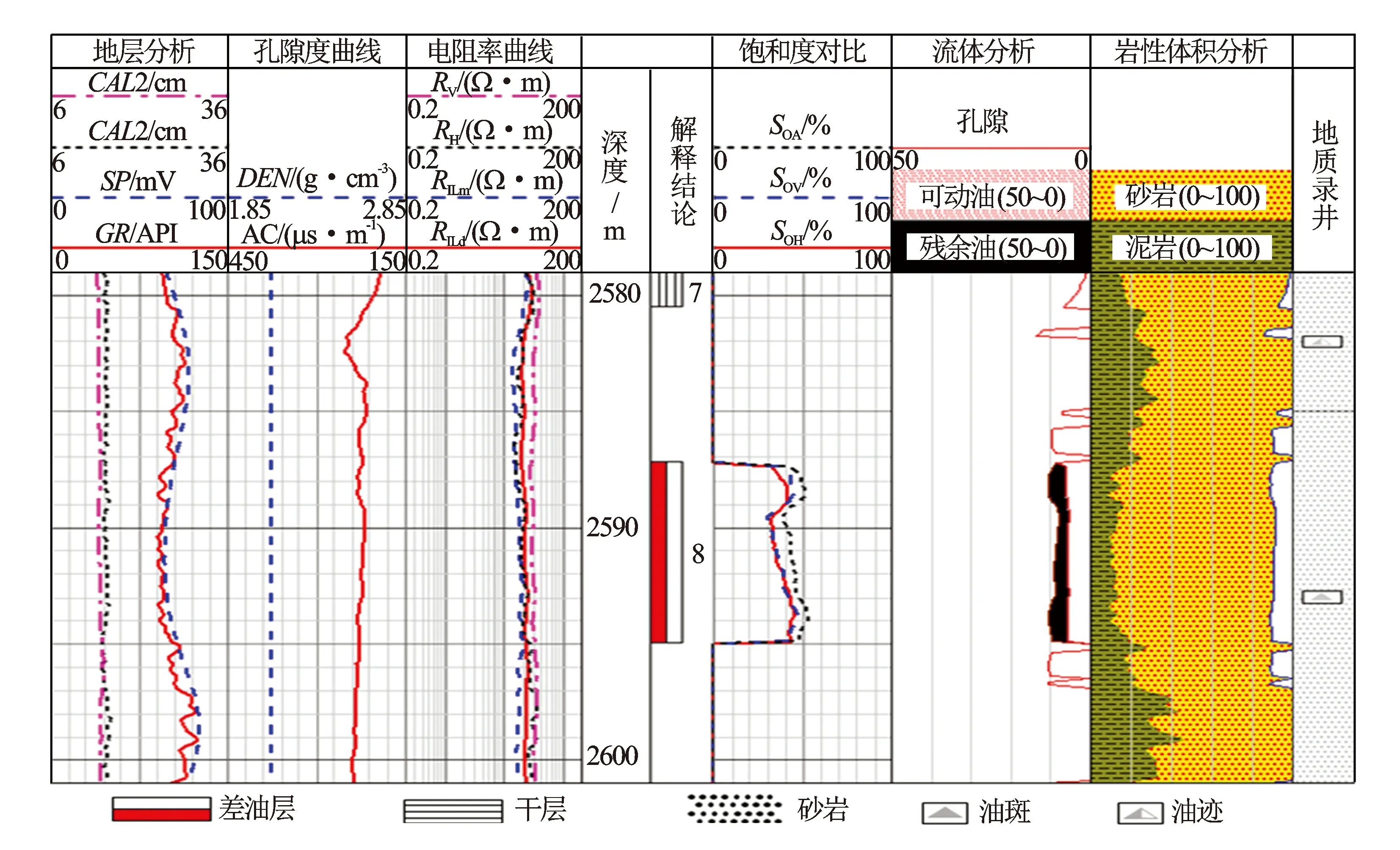
图9 HH74P1井2 587~2 595 m井段电阻率各向异性测井解释处理成果图
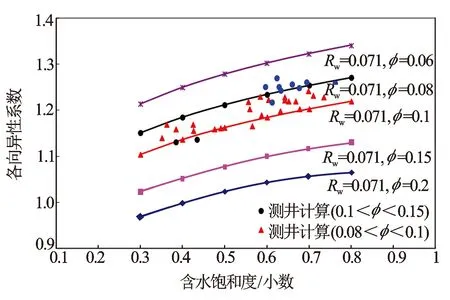
图10 ZY区块各向异性计算与实验模拟计算对比
3 结论及建议
(1)通过分析ZY区块水平样和垂直样岩电参数,总结了该区块岩电参数及各向异性变化规律,并与各向异性影响分析结果一致。
(2)基于Klein各向异性计算方法,结合ZY区块岩电参数分析,提出的“双岩电参数法”用于处理电阻率各向异性,应用效果明显,能有效利用常规电测井资料评价水平井各向异性储层的饱和度。
(3)电阻率各向异性计算时,未考虑泥岩各向异性。根据各向异性理论,当泥岩存在电阻率各向异性时,也会对储层真电阻率产生影响。因此,为了更加精确地评价水平井储层各向异性,下一步工作可从泥岩各向异性入手,研究泥岩各向异性对水平井常规电测井资料储层评价的影响。
