基于优化神经网络的空调系统未知类型故障诊断

2019-01-19丁新磊李绍斌谭泽汉郭亚宾陈焕新

制冷技术 2018年5期

丁新磊，李绍斌，谭泽汉，郭亚宾，陈焕新*

（1-华中科技大学能源与动力工程学院，湖北武汉 430074；2-空调设备及系统运行节能国家重点实验室，广东珠海 517907）

0 引言

近年来，空调系统在各领域中的应用越发普及[1]。由于工况的异常变化或长时间不间歇地运行等原因，空调系统会在非健康的条件下运行，这样会导致不同故障的产生[2]。故障的产生又会造成工作和生活环境的恶化及能源消耗的增加等问题[3-5]。制冷系统的充注量故障也会导致能耗的增加。因此，对其进行及时的故障检测与诊断就显得尤为重要[6-8]。

自数据驱动方法应用于制冷行业以来，学者们便不断地利用各种数据挖掘算法，研究制冷系统的故障检测及诊断[9-12]。在众多数据挖掘算法中，BP神经网络是一种多层前馈网络，它在训练过程中利用误差逆传播来调整权值、阈值，直至达到设定的目标，进而得到输入数据与输出数据之间的映射关系[13-14]。李志生等[15]使用真实测量的数据建立 BP神经网络模型，实现了对制冷机组故障的实时检测与诊断。石书彪等[16]优化了BP神经网络，利用贝叶斯正则化提高了网络的泛化能力，冷水机组的故障检测效率及诊断精度也得以提高。梁晴晴等[17]利用BP神经网络，建立了离心式冷水机组故障诊断模型，并通过贝叶斯归一化，改变隐含层层数和隐含层节点数进一步优化模型，得到了较好的诊断效果。

基于数据驱动方法的制冷系统故障诊断模型，大都是利用已知类型的故障数据进行网络模型训练，并对已知类型的故障进行诊断。若系统产生了未参与建模训练的故障类型数据，就无法做出准确的判断，可能将实际为未知类型的故障诊断为已知类型的故障，这样不利于准确地诊断出故障的种类，会对故障诊断的正确率产生较大的影响。针对这一问题，本文提出了一种优化的BP神经网络诊断策略。首先通过已知类型的故障数据建立BP神经网络模型，然后对模型的正确率进行验证，最后利用模型完成对未知类型故障的诊断。此策略可以诊断出未知类型故障。

1 实验简介

本文所有的实验都是在制冷工况下的焓差室中进行。图1为用于实验的多联机系统和其中一些主要传感器的示意图，此实验系统由1个室外机和5个室内机组成。室外机有1个过冷器。室内机有5个风机盘管。表1为系统的一些参数。

图1 实验用多联机系统图解

表1 多联机系统的相关参数

实验在5组不同充注量水平下进行，如表2所示，充注量水平的范围为63.64%至120.00%，其中包含了充注不足与过量的情况。此外，每组充注量水平的实验，都将在3种不同的制冷工况下进行，这3种不同工况分别为低温制冷、中温制冷和高温制冷工况。

在两个空气处理机组的调节下，实验时，室内外的温度和相对湿度如表3所示。在进行实验时，每次实验的时间至少持续45 min，实验数据测量的周期为15 s。所有的实验结果都由数据采集器收集。这些数据样本就构成了完整的数据集。

表2 5组充注量水平实验

表3 3种不同制冷工况

此次实验的主要目的是获得多联机系统的制冷剂充注量数据，用来对多联机系统进行分析。在本文中，此次实验获得的数据将用于未知类型的故障诊断。本文采用了5种充注量水平，将在第3章进行介绍。

2 故障诊断策略

2.1 BP神经网络

在实际应用中，约80%的模型使用了BP神经网络或其变化形式[18-19]。它在训练过程中利用误差反向传播算法对网络权值和网络阈值进行调整，直至网络误差平方和达到最小、效果达到最优。BP神经网络模型通常包含输入层、隐含层和输出层 3部分，图2为单隐层BP神经网络模型示意图。

图2 BP神经网络拓扑结构图

在图2中，X1、X2、…、Xn是输入值；O1、O2、O3、O4、…、Oj是隐含层输出值；Y1、Y2、…、Yk是最终输出值；隐含层前后分别为输入层的权值ωij、阈值qj和输出层的权值ωjk、阈值qk。利用网络输入值及训练得到的权值、阈值，可以计算出隐含层的输出为[20]：

在利用隐含层输出及训练得到的权值、阈值，可以计算出输出层的输出为：

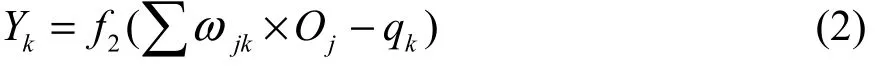
BP神经网络可以使用多种节点传递函数，常见的有线性传递函数 Purelin，对数 S型传递函数Logsig。BP神经网络能够使用的训练函数同样种类繁多，常见的有负梯度下降 BP算法训练函数Traingd、负梯度下降动量 BP算法训练函数Traingdm、Bayes规范化BP算法训练函数Trainbr等，本文选用的是函数Trainbr。在进行预测前，要先通过训练使网络具备联想记忆和预测能力[21]。

2.2 故障诊断流程

图3为本文提出的基于BP神经网络的故障模型的诊断流程图，它主要由两个部分组成，分别为模型建立与故障诊断。

第一部分故障诊断模型的建立。首先，从数据库中选取5种不同程度的制冷剂充注量数据，将其划分为两类，第一类作为已知类型的故障数据，用于训练与测试，它包含4种不同程度的制冷剂充注量数据。第二类作为未知类型的故障数据，仅用于测试，只包含1种不同于前4种程度的制冷剂充注量数据；然后，取第一类数据的60%作为训练数据，剩余的先分出15%用于验证模型，再分出25%与第二类数据混合作为测试数据；最后，初始化神经网络，对输入数据进行预处理，将处理好的数据输入BP神经网络中，训练网络，使其符合要求。在使用前4种不同程度的制冷剂充注量数据对模型进行训练时，所用数据应尽可能充足可靠，以增强所得网络的逼近和推广能力。

第二部分为使用第一部分得到的网络模型进行故障诊断。主要诊断原理如下：本文将神经网络的输出向量作为故障标签，其最大值所在的列数代表着不同的故障程度。因此，对于参与训练的已知类型故障，只需找到其输出向量的最大值所在，就能够确定其故障类型。对于未参与训练的未知类型故障，本文通过下文对训练数据的输出结果进行分析，确定了一个区分阈值，最大值若小于此值，则为已知类型的故障数据，若大于此值，则为未知类型的故障数据。利用 Logsig-Purelin函数确定此值所在的输出向量的计算公式如下：

式中：

ωij——输入层到隐含层的权值；

qj——输入层到隐含层阈值；

ωjk——隐含层到输出层的权值；

qk——隐含层到输出层的阈值；

Xi——某一次的输入数据，Xi的选取详见第 4章对训练数据的结果分析。

图3 未知类型故障诊断流程图

3 故障诊断模型的建立

3.1 故障诊断模型输入与输出变量的确定

3.1.1 故障诊断模型输入变量的确定

本文采用的数据是空调系统制冷剂充注量的故障数据。基于制冷系统热力学原理与数据挖掘分析，本文选择表4所示的18个参数作为优化模型的故障指示特征，这些参数能够反映出系统运行故障（健康状态）。

3.1.2 故障诊断模型输出变量的确定

本文选用的5种不同程度的故障数据如表5所示，其中包含了充注过量、适中和不足3种情况。表5说明了各故障对应的故障标签及其神经网络输出。其中故障1～4代表了4种不同程度的已知类型故障数据，故障5代表了第5种程度的未知类型故障数据。在神经网络输出的向量中，最大的数值越接近1，则表明越接近该种水平。如：（1 0 0 0）表示编号为1的120%故障水平，（0 0 0 1）表示编号为4的80%故障水平。

表4 优化BP网络模型的故障指示特征

3.2 网络结构的选择

由上文选择的18个特征参数，确定BP神经网络输入层的节点数为18，再由BP神经网络模型的输出向量，确定输出层的节点数为 4。隐含层的层数由映射定理分析可知[22]，本文采用单隐含层。对于拓扑结构的确定，HORNIK等[23]已经证明，隐含层若采用 Sigmoid函数，输出层配合其采用线性Purelin函数，则单隐层的网络能够以任意精度逼近任何有理函数。故本文采用的传递函数分别为Logsig函数和Purelin函数。BP神经网络隐含层节点数的确定也十分重要，对网络精度的影响很大：数量不足，学习效果不好；数量太多，容易过拟合。隐含层节点数的确定可参考式(4)：

式中，M代表输入层神经元的数量；L代表输出层神经元的数量；K值范围3到5，ΔA值范围4到10。式(4)仅可计算出大致范围，最佳节点数的确定，最终还要通过试凑法实现。

本文设置的网络训练次数为1,000次，学习率为 0.01，目标精度为 0.05，最小下降梯度为1.00×10-10，最大值为 1.00×10100。本文采用的训练函数是贝叶斯正则化的梯度下降BP算法训练函数Trainbr。选用的传递函数为Logsig-Purelin搭配。

表5 故障编号对应的故障水平及神经网络输出

4 结果分析与讨论

本部分主要针对训练数据、验证数据和测试数据这3组数据的输出结果进行分析。其中对训练数据的分析是为了更好地理解所得到的网络模型，理解已知类型故障数据的输出向量的特征；对验证数据的分析是为了验证模型的正确率；对测试数据的分析是最关键的，是为了区分出未知类型故障。

4.1 故障诊断模型训练数据的分析

针对用于训练的故障数据，用所得模型对训练数据进行模拟，分析其输出结果有助于理解网络模型，理解已知类型故障的特征，便于对未知类型故障进行区分，故这一步十分重要。表6用混淆矩阵表示训练数据的诊断结果。从表中可以看到，编号3故障误诊为编号2的数量最多，这是因为编号3代表的充注量程度与编号2代表的很接近，故障影响参数的输出也比较相似。

表6 训练数据输出的混淆矩阵

训练数据的详细诊断结果如图4所示。结合上表分析可知，对于训练数据，网络的效果比较好，误诊数不多，总的诊断正确率为89.04%。对编号4故障的诊断效果最好，其训练样本总数最多，且正确率也最高。对不同故障的神经网络输出进行分析，可以知道输出向量的最大值代表着故障类型。因此，对于训练数据的每个样本，本文取其输出向量的最大值，进行从小到大排序，然后取位于排序后95%位置的数据，代入式(3)中计算出区分阈值。对于测试数据的各个样本，取其输出向量的最大值与区分阈值比较，就能够确定故障的类型了。

图4 训练数据的样本总数、误诊数与正确率

4.2 故障诊断模型正确率的验证

选取故障1～4的15%用于模型验证。由于训练过程中仅存在4种故障类型，故此处验证的结果也只包含这4种故障。表7用混淆矩阵表示验证数据的诊断结果。

表7 验证数据输出的混淆矩阵

验证数据包含所有的已知故障类型，总的诊断正确率为88.62%。验证数据的详细诊断结果如图5所示。对比图4和图5，可以看到，验证数据的模型诊断结果与训练数据相近似，说明本文训练出来的网络对于二者有着相似的作用，认为模型是有效的，达到了验证的效果。

图5 验证数据的样本总数、误诊数与正确率

4.3 故障诊断模型对未知类型故障的诊断

在对网络模型进行了验证之后，就要诊断未知类型的故障，这一部分是本文的关键点。第2章中提到将故障 1～4的 25%和故障 5混合作为测试数据，这样测试数据中既包括参与训练的已知故障，又包括未参与训练的未知故障。由于此处加入了一种未知类型故障，故对应的故障种类增加到了5种，所得到的混淆矩阵同样产生变化，表8为其结果。从表中可以清楚地看到，实际种类为故障5的类型，被误诊为其他4种类型的数量并不多，实现了诊断未知故障的目的。

表8 测试数据输出的混淆矩阵

测试数据的详细诊断结果如图6所示，总的诊断正确率为88.56%。将其与图4、图5对比，可以看到，对于已知类型故障1～4，模型诊断结果与训练数据、验证数据的相似，区别在于编号1～4的故障都有少量被识别为第二类故障，也就是故障5。对于未知类型故障5，其误诊总数并不多，在可以接受的范围内，其诊断正确率达到99.48%，很好地诊断出了这种未参加网络训练的未知类型故障。