基于AHP法的石河子发电厂周边空气质量评价

张天毅，宁 川，王 健，苗世霞

(1.国网兰州供电公司，甘肃 兰州 730070；2.石河子大学 机械电气工程学院，新疆 石河子 832003;3.石河子大学 兵团空间信息工程技术研究中心，新疆 石河子 832003)

1 引言

近年来我国经济社会飞速发展，不断加快的工业化、城市化进程导致城市、农村大气环境污染问题日益突出[1]。以石河子为例，近些年秋冬季节大气环境污染问题突出，尤其是以PM2.5为主要污染物造成的雾霾问题，影响面积大、波及范围广、持续时间长，对当地大气环境质量造成了较为严重的后果。

环境评价可以揭示环境质量状况及其变化趋势，分析出污染治理的重点对象，为环境规划和环境综合治理方案提供依据[2]。空气质量评价体系具有单一指标不相容性，是一个多项指标共同参与决策的过程[3]，因此，迫切需要建立一个科学、综合且简便易行的综合评价方法对环境质量进行描述。针对环境质量等级评价方法，主要有层次分析法[4]、模糊综合评价法[5]、灰色关联分析法[6]、属性识别分析法[7]、T. L. Saaty提出的层次分析法[8]等。

层次分析方法在环境质量评价方面已经得到了广泛应用，并取得了理想效果。本文以石河子市阳光双语学院与石河子南开发区农田为实验区域，结合环境数据采集设备采集到二氧化碳、一氧化碳、PM2.5浓度数据，选择使用基于模糊原理的AHP法对实验区域进行空气质量评价模型的构建，并将实验结果与其他方法对比，取得了较为理想的结果，为今后在空气质量评价方法的应用研究提供一定的借鉴意义。

2 数据处理方法

2.1 数据预处理方法

2.1.1 格拉布斯准则

平台在采集观测数据时往往存在一些大误差数据，影响整个实验结果分析的正确性，为此，可以采用格拉布斯准则[9]剔除此类数据。粗大误差数据剔除后继续利用准则判断，直至满足准则。样本数据中是否存在大误差数据，可由下式完成判断：

|Si|=|Xi-Xav|>G(n,Pa)·δ标准

(1)

在式(1)中，δ标准：样本数据标准差；G(n，Pa)：格拉布斯常数；Pa：置信度，文中取0.95。

2.1.2 相关系数

若有a、b两组数据，其平均值为分别为a1、b1。定义皮尔逊积矩相关系数[10]R为样本数据协方差和标准差之间的比值，如下式(2)：

(2)

R的值与1越接近，相关性越好，拟合结果越准确。

2.2 AHP法理论

基于层次分析与模糊学相结合的AHP法[11]在空气质量模型构建中效果较好，其具体算法流程如下：

2.2.1 因子集的选取

评价因子集的建立通过选择二氧化碳、一氧化碳、PM2.5，如下式所示：

X={x1(CO2),x2(CO),x3(PM2.5)}

(3)

空气质量标准数据以官网为准。

2.2.2 评价指标集建立

按5个分级基准将空气质量划分为清洁、无污染、轻度污染、中度污染、重度污染，分别用y1、y2、y3、y4、y5表示，每个选定的评价因子yi对应一个标准数据，假定标准数据为si。构建环境质量评价级Y与si关系有：

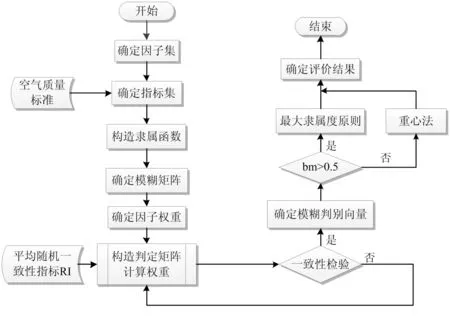
图1 AHP算法流程

(4)

2.2.3 构造隶属函数

选择隶属函数，确定隶属关系uij(参考文献[11])。

2.2.4 确定模糊矩阵

根据隶属函数，可得模糊矩阵如下式(5)：

(5)

2.2.5 各因子权重计算

因子权重计算过程如下：

(1)判别矩阵Q建立。假定系数集A为：

A={A1,A2,A3,A4}

(6)

Ai表示第i中某因子观测值比官网标准值，判别阵与A有以下关系式(7)。

(7)

(2)权重计算。计算A各行元素乘积：

(8)

计算Fi的n次方根：

(9)

归一化向量：

(10)

计算矩阵最大特征根：

(11)

(3)检验一致性。对A采用CR判断其一致性，根据因子数，RI取值为0.5258。

2.2.6 模糊向量计算

评判向量X与F之间有以下关系：

X=F°M

(12)

2.2.7 结果分析

模糊评价向量X={x1，x2，x3，x4，x5}，取xm为x1，x2，x3，x4，x5中最大值，xm>0.5时，xm即为对应等级；xm≤0.5时，按下式计算。

(13)

3 实验方案与数据预处理

3.1 实验方案

采集实验总共选择了两个采集区域，分。第一个是石河子市阳光双语学校，第二个是石河子南开发区热电厂。数据采集过程以30s为一个周期，采集十组数据取其平均值作为样本数据，并选取同时段的官网数据作为对照[12]。数据采集区域如下图2a、图2b所示。

图2a 阳光双语学校

图2b 南区热电厂

3.2 实验数据预处理

3.2.1MG811电势差与浓度函数关系

查阅文献[12]可得，MG811型传感器的灵敏度特性曲线可分为两个区间，数据值如下表1所示。

表1 区间拟合参数

选取指数函数关系对上表数据进行曲线拟合，结果如图3。

由上图结果可得:浓度与电势差之间的函数关系满足下式(14)、(15)：

区间1：

(14)

区间2：

(15)

根据上式关系求得区间1、2上的决定系数分别为R1=0.996、R2=0.997，标准差分别为RMSE1=3.699、标准差RMSE2=0.771，满足拟合条件，因此可根据式(14)、(15)函数关系将电势差转换为浓度值(注：二氧化碳标准数据单位为%，本文中单位为ppm，因此需要转换单位)。转换关系如下式(17)：

|Si|=|Xi-Xav|>G(n,Pa)·δs

(16)

C=P/10000

(17)

3.2.2DSM501低脉冲率与粒子数函数关系

采集到的样本数据不可避免会存在粗大误差值，因此要对其进行剔除。剔除粗差后得到的样本数据如下表2。

a 区间1拟合结果

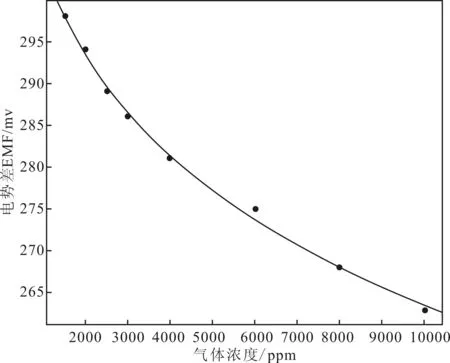
b 区间2拟合结果图3 MG811电势差与浓度关系

通过最小二乘法对上表数据中的低脉冲率和标准浓度值进行拟合，得到如下图4所示曲线。

由上图可得，低脉冲率和标准浓度数据之间存在一元线性关系。为保证拟合关系的正确性，利用式(2)关系计算相关系数R，结果见下表3。

表2 样本数据

图4 DSM501A低脉冲率和标准浓度值拟合表3 相关系数计算结果

对象SD观测值(单位:“1”)SD标准值(单位:μg/m3)协方差(单位:μg/m3)RPM2.52.165239.096510.450.986

根据表(3)结果，相关系数R=0.986，比较接近1，说明两组数据相关性较好，且满足一次线性函数关系，由此得如下式(18)：

y=0.0089×x+0.059

(18)

3.2.3MQ-7电势差与浓度函数关系

将MQ-7气体传感器采集的多组实验数据剔除粗大误差，得到表4所示数据。

通过最小二乘法对上表数据中的电势差和标准浓度拟合，得到如下图5所示曲线。

根据图5所示结果，得到函数关系如下式(19)：

y=0.00008×x2-0.172×x+1.333

(19)

根据拟合结果得到方差0.129，决定系数0.976，标准差0.078，能准确地反映测量值与官网标准值之间的函数关系。

4 AHP环境质量等级评价模型评价

4.1 环境等级评价模型验证

空气质量等级评价模型的准确性需要进行验证。本文随机选取了样本组数据中的3号样本数据最模型可靠性进行验证，验证结果如下表所示。

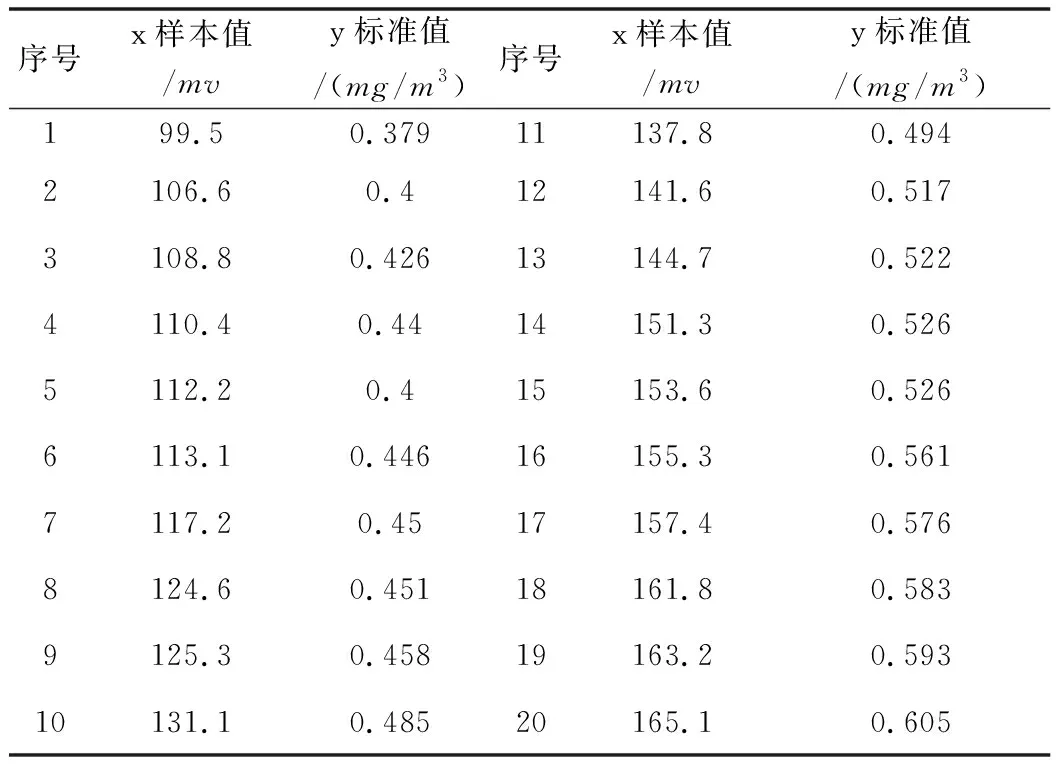
表4 样本数据与官网数据对照

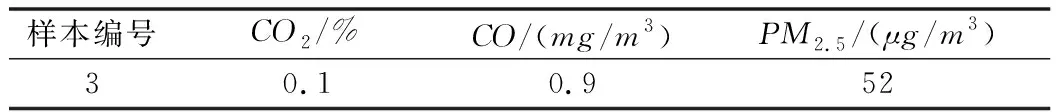
表5 示例数据

根据公式(6)—(11)计算可得：评价向量X=[0.340.66 0 0 0]T，权重E=[0.52 0.12 0.36]T。参考最大隶属度原则，取xm=0.66，则空气质量等级为无污染，结果可靠。

图5 MQ-7电势差和标准浓度值拟合曲线

4.2 AHP评价模型验证结果分析

绘制实验采集的30组数据评价结果统计图，如下所示。

图6 样本数据评价结果统计

针对采集的30组实验数据，分别将用AHP评价法建立的环境等级评价结果和官网公布的空气污染等级进行对比验证。根据单因子设制原则，本文将清洁、无污染等级视为合格，用“0”表示；轻度污染、中度污染、重度污染视为不合格，用“1”表示[12]。根据上图分析，在30组样本数据中，有28组数据的结果与官网公布空气质量等级一致，只有“11”、“23”号不一致，准确率达到93.33%，由此证明了该方法可用性和准确性。

5 结语

本文针对采集到的石河子市及发电厂周边二氧化碳浓度、一氧化碳浓度、PM2.5浓度值数据，采用了AHP法建立了空气质量评级模型，对试验区域的空气质量等级进行了评价，并与单因子分析法对比验证其可靠性，效果较为理想，具有一定参考意义。但针对本文的研究方案在环境等级评价方面仍具有局限性：①实验过程只采集了二氧化碳、一氧化碳、PM2.5这三种污染物作为评价因子，评价因子种类较少，不具备多样性；②实验验证只是与单因子评价法进行了对比，并没有与AQI指数实现对比验证；③鉴于AHP法在评价过程中确立的指标体系需要有专家系统支持，给出的指标是否合理决定了评价模型的准确性。

针对以上不足，今后仍需在评价因子选取多样性、多重评价模型验证对比、AHP法指标体系的优化算法设计等方向继续研究。