Effects of airfoil scaling on the predicted aerodynamic performance and forcing of turbine

JIANG Jinpeng, SHI Jingcheng, SU Lichao, GONG Fan, WANG Jue

(1. Science and Technology on Space Physics Laboratory, China Academy of Launch Vehicle Technology, Beijing 100076, China;2.China Academy of Launch Vehicle Technology,Beijing 100076, China)

Abstract：Effects of vane/blade airfoil scaling on the prediction of aerodynamic performance and unsteady forcing have been investigated for the turbine. A single-stage axial-flow turbine with 18 vanes and 32 blades was adopted. 3D steady and unsteady simulations were conducted for configurations with different scaling factors, and the full-scale case was used as the baseline simulation. The results show that the vane/blade airfoil scaling has little influence on the steady and time-averaged pressure on the blade and performance of turbine. The predicted deviation is below 2% even if the scaling deviation exceeds 10%. The fast Fourier transform (FFT) is used to transform the unsteady pressure and forcing predicted in the time domain to obtain the characteristics in the frequency domain. The vane/blade airfoil scaling has little difference on the frequency characteristics of unsteady pressure and aerodynamic forces, while amplitude is greatly affected. The results show that the predicted amplitude deviation is not directly related to the scaling deviation, but the case with small scaling deviation (3.125% in this study) indeed shows relatively stable and minor error.

Keywords：airfoil scaling; numerical simulation; aerodynamic performance; aerodynamic forcing

0 Introduction

The flow in turbomachines is highly unsteady and turbulent because of the aerodynamic interaction between the adjacent rows due to effect of wakes and potential flow field. The unsteady flow connects with aerodynamic performance and structural integrity of the turbine. Many attentions have been paid to the understanding of unsteady flows in turbomachines, which is necessary for advanced design and analysis.

As CFD techniques developing and reaching a high degree of sophistication, it is becoming a powerful tool for the analysis of unsteady flows, and numerical simulation has been widely conducted to study the unsteady flows in turbomachines. The influence of clocking on unsteady forces of turbine blade[1]and effects of axial gap on unsteady flow[2-4]were investigated using numerical simulations. Numerical simulation of turbine flow field was also useful in turbine design, which was adopted in the design optimization for turbine cascades[5-7]. Aerodynamic analysis and optimization of a compressor with casing grooves was conducted to improve operating stability using numerical simulation[8]. Simulations for the turbomachine stage over the entire circumference (360 deg) can account for both global and local unsteady effects. And the 360 deg modeling allows for any arbitrary blade count ratio of the adjacent rows. However, these simulations cost too excessive in computation and time, and they are not always possible to be conducted even with large massively parallel computer systems. Therefore, simulations for turbomachine flows are usually performed with reduced circumferential period models assuming periodic flows. When the blade counts in adjacent rows can be divided by some common factor, simulations can be conducted with a reduced circumferential period that is common to all rows in the configuration exactly[3, 9]. The reduced circumferential period is usually kept as small as possible to minimize the computational costs. Unfortunately, there is not always a common factor among the blade counts in adjacent rows. An approach is to modify the blade counts and scale the blade rows as little as possible, such that spatial periodicity is achieved and reduction in the circumferential period is allowed. This approach is widely adopted when conducting numerical simulation for flows in turbomachines.

Numerical simulations of the unsteady flow in an axial compressor were performed to investigate the mechanisms involved in driving rotor wake oscillation[10]. Unsteady three-dimensional simulations were conducted to investigate the influences of varying specific heats on the performance of a supersonic turbine[11]. Three-dimensional unsteady simulations were performed to study the unsteady flow phenomena at off-design operating conditions[12]. The simulations showed reasonable agreement over a wide range of flow conditions. Turbine blade surface pressure distributions have been investigated through experiments and numerical simulations[13]. The time-averaged and unsteady simulation results showed good agreement with the experimental data at the design operating conditions. Two-dimensional simulations were conducted to investigate unsteady aerodynamic force on blades in a partial admission supersonic turbine stage[14]. The scaling technique was adopted by investigations mentioned above, however, not accounting for to what extent the scaling influencing the flow.

Aerodynamic performance and unsteady characteristics of turbomachines are concerned about by researchers. To investigate the effect of airfoil scaling on the predicted aerodynamic performance and unsteady characteristics, five cases with different scaling factors for a one stage turbine with 18 vanes/32 blades were employed, and steady and unsteady simulations were conducted. The stator vane and rotor blade were scaled alone. The vane/blade airfoil scaling has little influence on the turbine performance including power and efficiency in a large range of scaling factor. Frequency characteristics of unsteady pressure and aerodynamic forces are rarely affected by vane/blade airfoil scaling. Amplitudes of harmonics are greatly affected by scaling. The case with small scaling deviation (3.125% in this study) shows relatively stable and minor errors of harmonic amplitudes.

1 Numerical models

The model investigated in this work is a one-stage axial turbine developing for a new high-thrust rocket engine. 3-D steady and unsteady RANS equations were solved by the commercial code ANSYS-CFX 14.5. The computational grids were generated by the IGG/Autogrid software package. The total pressure and total temperature were specified at the inlet, while the static pressure was imposed at the outlet. The rotational speed of the rotor was 16 000 rpm. Frozen rotor boundary was adopted between the stator and rotor in steady solver, while transient rotor stator interface was used in unsteady solver, and the steady simulation results were used as initial values of unsteady simulations. Rotational periodic boundary conditions were employed when reduced circumferential period was used. No-slip and adiabatic conditions were enforced along all the solid surfaces. The shear stress transport (SST) turbulence model was employed, since it can produce relatively accurate simulations for flow separation under adverse pressure gradients. The SST model blends thek-ωmodel in the near-wall region and thek-εmodel in the bulk domain. 50 time steps were used to rotate one blade past one vane passage. The numerical method and computational codes have been validated by Kim et al.[8]and Sakai et al[15]. In Kim’s study, results show some uniform underestimations of the total pressure ratio and adiabatic efficiency, but are in good qualitative agreement with the experimental data. In Sakai’s study, the computational pressure distribution at nozzle outlet is in good agreement with experimental pressure distribution. The numerical method is believed to be effective in flow simulation of turbomachines.

1.1 Grid-independency

The mesh for a single stator passage and a single rotor passage are shown in
Fig. 1. As can be seen, structured grid systems were created in the computational domain with O-type grids near the blade surface and H-type grids in the other regions. Since the full annual simulations require very large computational costs and long time, grid-dependency test was performed by simulating the steady flow of the reduced model consisting of one stator passage and two rotor passages with various numbers of grids.
Fig. 2 shows the comparison of steady flow total to total efficiency. The total-to-total efficiency of the turbine is defined as:

(1)

Where theTt0，pt0are total temperature and total pressure at the inlet;Tt2，pt2are total temperature and total pressure at the outlet, andγis specific heat ratio. It can be seen from
Fig. 2 that efficiency in the fourth case is almost the same with the fifth, and the difference between the third and the fifth cases is less than 0.2%. Mesh of the third case was selected for the following simulations, taking account of the computational costs and accuracy.

Fig.1 Simulation mesh

Fig.2 Grid independency check in terms of the total-to-total efficiency

1.2 Scaling configurations

Five groups of simulations have been conducted with different passage counts per row. The simulation without blade scaling was performed in one case. Two simulations were conducted with stator vane scaled and the other two simulations were performed with rotor blade scaled. The vanes were scaled by a factor of 18/16 and 18/20 respectively while blades were the same as the original model in the vane scaled cases. The blades were scaled by the factor of 32/33 and 32/36 respectively while vanes were not scaled in the blade scaled cases. The simulation configurations are presented in Tab.1. The scaling factor is defined as the number ratio between original blade and the scaled blade, expressed as following:

(2)

To describe the relative scaled deviation, the scaling deviation is defined as following:

(3)

To keep the pitch to chord ratio constant, the varied vanes/blades were scaled by the scaling factors. A comparison of the blade airfoils is shown in
Fig. 3. When the stator vane was scaled, the vane airfoils were aligned at the trailing edge. When the rotor blade was scaled, the blade airfoils were aligned at the leading edge. The axial gap between the stator and rotor was kept unchanged.

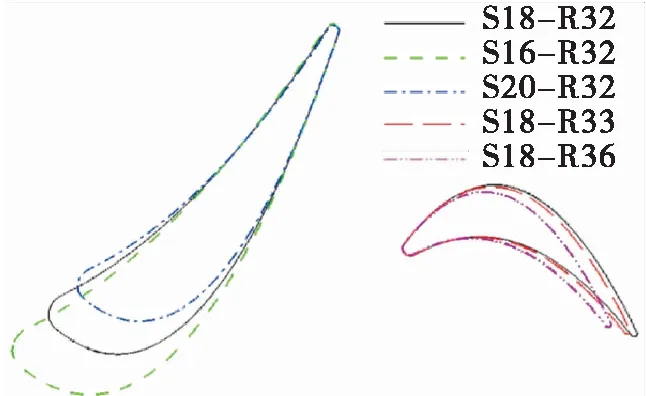
Fig.3 Stator and rotor geometry for different scaling cases

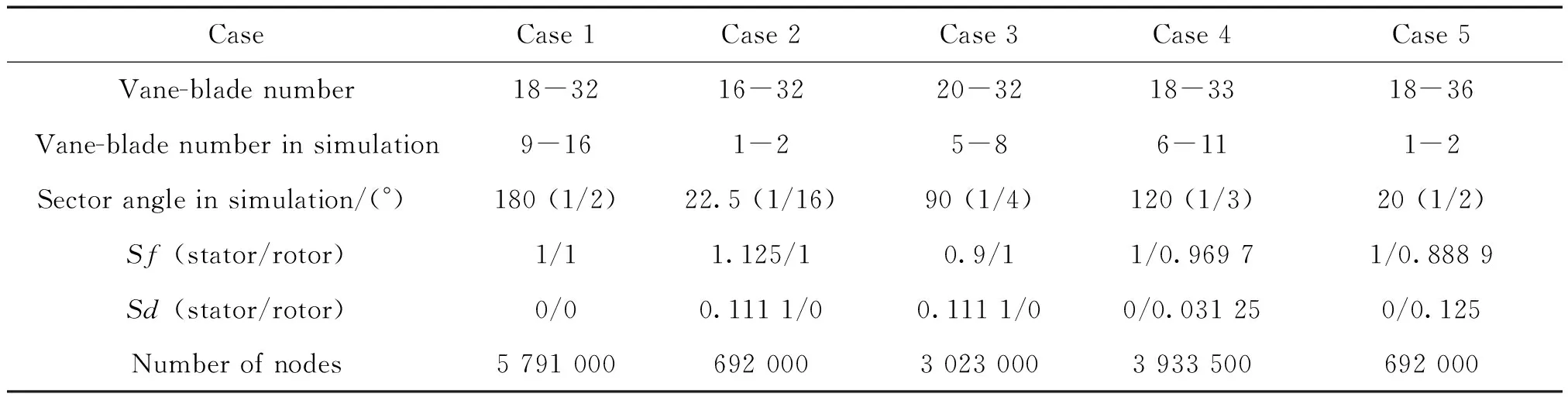
CaseCase 1Case 2Case 3Case 4Case 5Vane-blade number18-3216-3220-3218-3318-36Vane-blade number in simulation9-161-25-86-111-2Sector angle in simulation/(°) 180 (1/2)22.5 (1/16)90 (1/4)120 (1/3)20 (1/2)Sf (stator/rotor)1/11.125/10.9/11/0.969 71/0.888 9Sd (stator/rotor)0/00.111 1/00.111 1/00/0.031 250/0.125Number of nodes5 791 000692 0003 023 0003 933 500692 000

2 Results and discussion

Steady, unsteady and unsteady time-averaged simulation results are analyzed in this section. The case S18-R32 with blade unscaled is used as the baseline simulation.

2.1 Steady results

Turbine efficiency is defined as ratio of the turbine specific work to the adiabatic work, expressed as following:

(4)

(5)

(6)

is the mass flow rate；Ris the gas constant andp2is the static pressure at the turbine outlet.

Turbine specific work and efficiency in different cases are shown in Tab.2. Results in case S18-R33 has the least deviation from the unscaled case, which is only 0.075%. The other scaled cases give larger deviations. The maximum deviation in case S16-R32 reaches 2%.

Tab.2 Simulation results for different cases

Total pressure along spanwise at the exit of stator vane (5 mm downstream of the trailing edge) is shown in
Fig. 4. Since there are no upstream blade rows disturb the flow, the total pressure profile at the exit of stator vane is almost flat along the span. Total pressure decreases at 5% span near the hub and at 95% span near the tip influenced by end walls, which are boundary layers. Total pressure profiles in scaled cases have the same shape with the unscaled case. Pressure profile in S16-R32 is in excellent agreement with the unscaled case, while the total pressure in S20-R32 has obvious difference. This may indicate that the flow is more sensitive to the blade size decreasing, compared with the size increasing. Though having different scaling factors, the S18-R33 and S18-R36 cases have the nearly same total pressure profiles which are close to the unscaled case. This occurred because the downstream blade scaling has little influence on the upstream flow in the steady simulation. Though the case S20-R32 has the largest deviation from the unscaled case, the difference between them is just within 0.8% in main flow area.

Fig.4 Total pressure comparison,5 mm behind the trailing edge of stator

Total pressure along spanwise at the exit of rotor blade (5 mm downstream of the trailing edge) is shown in
Fig. 5. Influenced by the upstream rotor rows, total pressure profiles are more complex than those at the exit of stator vane. The boundary layers near both end walls are thinner compared with those at the exit of stator vane. Simulations in most scaled cases have similar trends with the unscaled one except the scaled case S18-R36. The case S18-R36 has several positions where total pressure loss occurred. The flow at downstream of the rotor blade was obviously affected by the decreasing blade size. Total pressure profile in case S18-R33 has the closest trend to the unscaled case, while the total pressure is slightly higher than the unscaled case. The case S16-R32 has greater total pressure loss caused by hub passage vortex (shown in
Fig. 6) than the unscaled case around 20% span, and it has higher total pressure peak around 2% span. The simulation in case S20-R32 captured similar trend with the unscaled case, while total pressure is lower. The location that total loss peak occurred (25% span) is slightly differs from the unscaled case (20% span). In general, relatively great difference was found between the case S18-R36 and the unscaled case as expected because it has the largest scaling deviation. Though having the same scaling deviation, the case S20-R32 has larger difference than the case S16-R32. It shows similar characteristic with the total pressure at the exit of vane. The predicted pressure difference between the scaled case S20-R32 and unscaled case is below 1.2%.

Fig.5 Total pressure comparison, 5 mm behind the trailing edge of rotor

Influenced by the upstream vanes, pressure on different blades differs. The pressure envelopes at midspan are shown in
Fig.7. Pressure profiles on the pressure sides are in good agreement. Pressure profiles on the suction side within 20% chord differ a lot, while good agreement is reached at the other span. Within 20% chord, the S18-R33 case gives the best agreement, while the S18-R36 has the most deviation from the unscaled case.

Fig.6 Rotor hub passage vortex (case S16-R32)

Fig.7 Comparison of pressure envelopes at blade midspan

2.2 Time-averaged results

Time-averaged total pressure along spanwise at the exit of stator vane (5 mm downstream of the trailing edge) is shown in
Fig. 8. The total pressure profiles show similar characteristics as those in steady simulations. The total pressure profile in S16-R32 is in excellent agreement with the unscaled case, while the total pressure in S20-R32 obviously deviates from the unscaled case. The maximum difference between the case S20-R32 and unscaled case is 1%. The S18-R33 and S18-R36 cases have the nearly same total pressure profiles which are close to the unscaled case.

Fig.8 Time-averaged total pressure comparison, 5 mm behind the trailing edge of stator

Time-averaged total pressure and total temperature along spanwise at the exit of rotor blade (5 mm downstream of the trailing edge) are shown in
Fig. 9 and
Fig. 10. All cases have similar trends with the unscaled one. There are all strong total pressure loss around 30% span induced by rotor hub passage vortex. The greatest difference occurs between the case S20-R32 and the unscaled case, and the maximum difference in main flow area is under 1%. Time-averaged total pressure profile in case S16-R32 is in good agreement with the unscaled case. It reveals that though having the same scaling deviation, the case S20-R32 has much larger deviation than the case S16-R32. Total pressure profiles in case S18-R33 and S18-R36 are similar. They are both close to the unscaled case and have slightly higher total pressure.

Fig.9 Time-averaged total pressure comparison, 5 mm behind the trailing edge of rotor

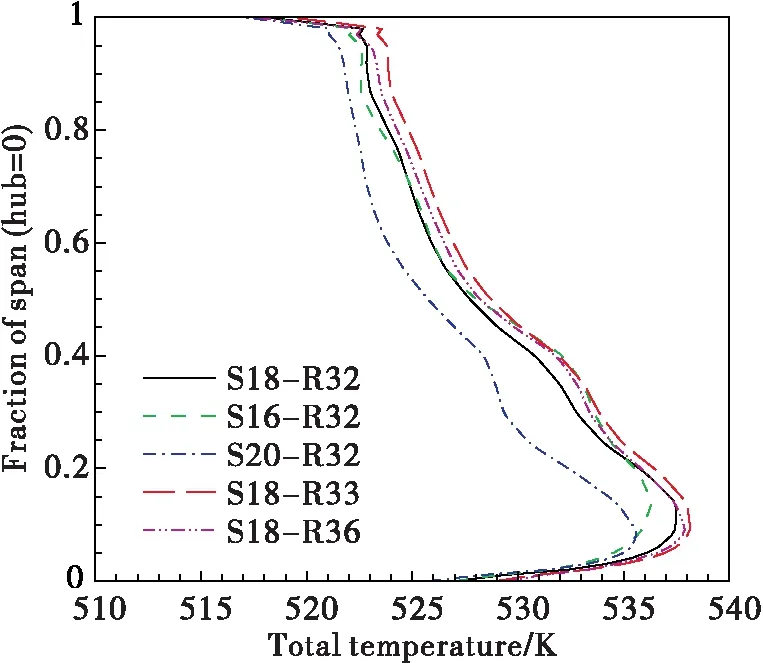
Fig.10 Time-averaged total temperature comparison, 5 mm behind the trailing edge of rotor

The time-averaged pressure profiles at midspan are shown in
Fig. 11. Pressure profiles in scaled case are mostly in good agreement with that in unscaled case. The S20-R32 case has a slightly obvious deviation from the unscaled case, and the maximum deviation on the suction side around 3% chord is below 2%.

Fig.11 Time-averaged pressure comparison at blade midspan

2.3 Unsteady results

The unsteady pressure is critical in determining the peak stress and whether resonance can be induced. The unsteady pressure signals predicted in the time domain are transformed using fast Fourier transforms (FFT) to obtain characteristics in the frequency domain. Results show that the harmonics are multipliers of the vane passing frequency (VPF). The frequencies in different cases are normalized by their own VPF.

Fig. 12 shows the FFT results of three points at different chordwise at midspan on the pressure side in different cases. It reveals that the first harmonics are dominant in all cases and positions. The scaled cases have similar frequency characteristics with the unscaled case. The amplitudes in different cases differ a lot. The amplitudes of 1stharmonic of the case S16-R32 are close to the unscaled case near the leading edge and trailing edge, while the deviation is much larger at mid-chord. The amplitudes of 1stharmonic of the case S20-R32 are much smaller than the unscaled case. This may result from the increasing vane number, which makes the flow field at rotor inlet more uniform. The case S18-R36 has large deviation from the unscaled case near the leading edge. The case S18-R33 generally has stable closer amplitudes of 1stharmonic at different positions. As for amplitudes of 2ndharmonic, the case S18-R33 gives close results with the unscaled case. Results indicate that vane/blade scaling has a little influence on frequency characteristics, however, the local unsteady pressure amplitudes are significantly affected.

Fig.12 Pressure harmonics of points

Aerodynamic forces on the rotor blade are calculated as following:

(7)

(8)

Fig. 13 shows the FFT analysis results of unsteady aerodynamic forces on the rotor blade. As can be seen, the aerodynamic force harmonics are multipliers of the vane passing frequency, and the amplitude of the 1stharmonic is much great than the other harmonics, especially the tangential forces. The case S18-R36 shows good agreement with the 1stamplitude, though it has a relatively large scaling deviation. The case S20-R32 still has the greatest difference from the unscaled case.

Fig.13 Harmonics of aerodynamic forces on the rotor blade

Fig. 14 shows deviations of 1stharmonic amplitude between the scaled cases and the unscaled case. As we can see, deviations vary a lot in different cases and for different variables. The case S20-R32 gives predicted deviations more than 50% for all variables. The case S16-R32 has small deviations for pressure near the leading and trailing edge, while has deviations more than 25% for the other three variables. The case S18-R33 has predicted deviations all below 20%. The case S18-R36 has predicted deviations below 11% except for the pressure near the leading edge. Amplitude deviations seem not to be directly related to the scaling deviation, however, the case S18-R33 with small scaling deviation indeed shows relatively stable and minor deviation.

Fig.14 Comparison of 1st VPF harmonic amplitude

3 Conclusion

3D steady and unsteady flow simulations of a one stage axial-flow turbine have been conducted for configurations with different scaling factors, to investigate effects of airfoil scaling on the predicted aerodynamic performance. A scaling deviation is defined to reflect the amount of scaling. The unscaled case was used as the baseline simulation. Results show that:

1) Generally, airfoil scaling has little effect on steady and unsteady time-averaged simulation results. The predicted errors of turbine specific work, efficiency and pressure are below 2% even when the scaling deviation is over 10%. This indicates that scaling can be an effective method in steady and unsteady time-averaged performance prediction, which could greatly reduce computational costs.

2) The harmonics of unsteady pressure and aerodynamic forces are multipliers of the vane passing frequency (VPF) and the first harmonics are dominant in all cases. Frequency characteristics of unsteady pressure and aerodynamic forces are rarely affected by vane/blade airfoil scaling. Amplitudes of harmonics are greatly affected by scaling.

3) Predicted amplitude deviations seem not to be directly related to the scaling deviation, however, the case with small scaling deviation indeed shows relatively stable and minor error. This indicates that scaling technique should be employed with caution, when investigating the unsteady amplitude characteristics. The scaled model is better to be close to the original model as possible.