根轨迹法在数字控制系统的应用研究

韩 巍



根轨迹法在数字控制系统的应用研究

韩 巍

（武汉船用电力推进装置研究所，武汉 430064）

本文以直流伺服电机为例，介绍了根轨迹在有传递函数和状态空间两种状况下在数字控制系统的具体应用。应用于传递函数时，由于校正器零极点对输出性能影响很大，因此需要不断对系统的根轨迹进行改进，这种方法依赖经验，但是计算简单，易于工程实践。应用于状态空间时，根据控制系统的性能指标确定闭环系统的主导极点，调节器参数与闭环系统的性能指标建立了量化关系，设计过程概念清晰，简洁明了，但是计算量比较大。

根轨迹 数字控制 传递函数 状态空间

0 引言

根轨迹法自从1948年被W.R.Evans提出以后，由于其用作图的方法表示特征方程的根与系统性能之间的关系，不直接求解特征方程，简单易行，在控制系统的分析与设计中得到广泛的应用。根轨迹法具有直观的特点，利用系统的根轨迹可以分析结构和参数已知的闭环系统的稳定性和瞬态响应特性，还可分析参数变化对系统性能的影响。在设计线性控制系统时，可以根据对系统性能指标的要求确定可调整参数以及系统开环零极点的位置，因此根轨迹法可以用于系统的分析与综合。另一方面，由于数字控制相对于模拟控制有许多优越之处，特别是近几年随着处理器等微电子技术突飞猛进的发展，数字控制的硬件平台日益更新更加快数字控制的推广应用，使之受到广泛关注。由于数字控制存在采样、保持等环节，其控制设计和模拟控制有很大不同，因而，研究根轨迹法在数字控制系统的应用很有必要。本文将以直流伺服电机为例，分别介绍根轨迹在传递函数和状态方程这两种描述方法下的具体应用，并比较其优缺点。

1 直流伺服电机控制

1.1 直流伺服电机控制模型

直流伺服电机电枢电压由反电动势和内阻压降两部分组成。其中，内阻压降等于电枢电阻乘以电枢电流，由于电枢电阻为常数，内阻电压与电枢电流成正比；电机转速和反电动势成正比，直流伺服电机转速控制可以等效为反电动势电压的控制。反电动势无法直接控制，需要由电枢电压间接控制，此时电枢电流可以理解为扰动信号。

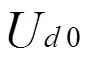
本文研究对象直流伺服电机=0.2W，C=10/41，T=14/41，则图1可以转化为图2的形式。

图1 额定励磁下直流伺服电机的动态结构图

图2 额定励磁下直流电动机的函数图

1.2 传递函数下的控制模型

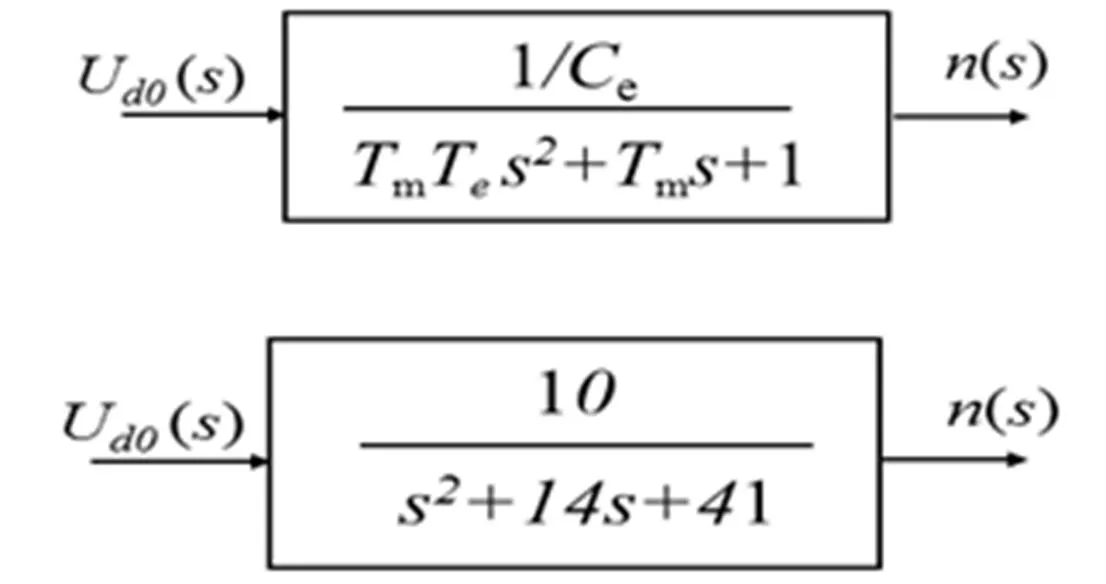
图3 Ial = 0时动态结构图的简化形式与传递函数

1.3 状态空间下的控制模型

式中，

在数字控制下，常常采用零阶保持器（ZOH）。采用周期采样的离散方式，采样周期设为T时，经过零阶保持器后，逆变器连续时间状态方程式（1）离散化后，可得：

2 根轨迹法在传递函数的应用

数字控制器有两种设计方法:模拟化方法和直接数字法。在采样周期足够小的情况下，把基于连续系统设计的模拟控制器离散化来得到数字控制器，为模拟化方法。但是，这种数字控制器设计方法只是一种近似处理，不能实现只有数字控制特有的控制策略。直接数字法就是对加采样保持器的被控对象离散化模型进行数字控制器设计。直接数字法在保持系统稳定的同时可得到更宽的控制带宽，这个优点在多环系统或采样周期较大时变得更为显著，所以数字控制器最好采取直接数字化方法设计，本文就采取这种方法。

2.1 被控模型的离散

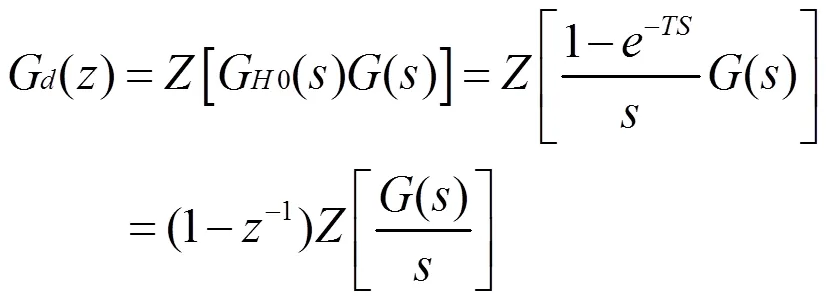
针对本研究对象直流伺服电机，可得：

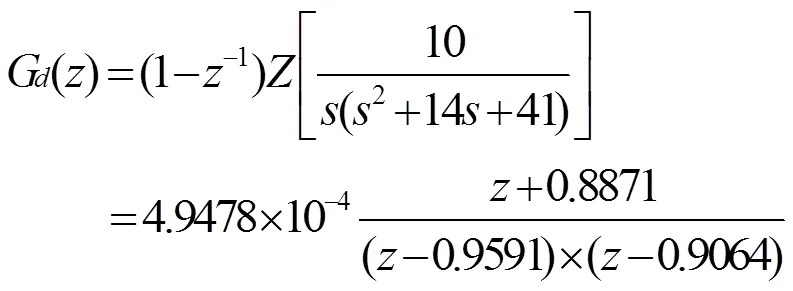
2.2 离散根轨迹设计

离散根轨迹的设计分为以下几个步骤：

a根据性能要求，确定闭环极点的允许范围；

b获得控制对象离散模型；

c根据纯比例控制的根轨迹，选择校正器；

d设计()，并反复循环修改。

本文研究对象超调、稳定时间的要求为，T£0.015 s，£2，=0.01s ；运用matlab画出仅为比例控制的根轨迹如图4所示。

可以看出，纯比例控制时，系统很容易不稳定，况且无论K取何值，闭环极点都不可能进入期望的区域，本文以超前校正为例讨论根轨迹在传递函数校正的应用，当考虑适当抵消=0.9591时的极点，则超前校正器可以形如(-0.9594)/(-))的形式[2]。图5是pole逐步向（-1，0）靠近，分别取值{0.6146，0.1146，-0.1146，-0.4146，-0.8146}时的根轨迹图。

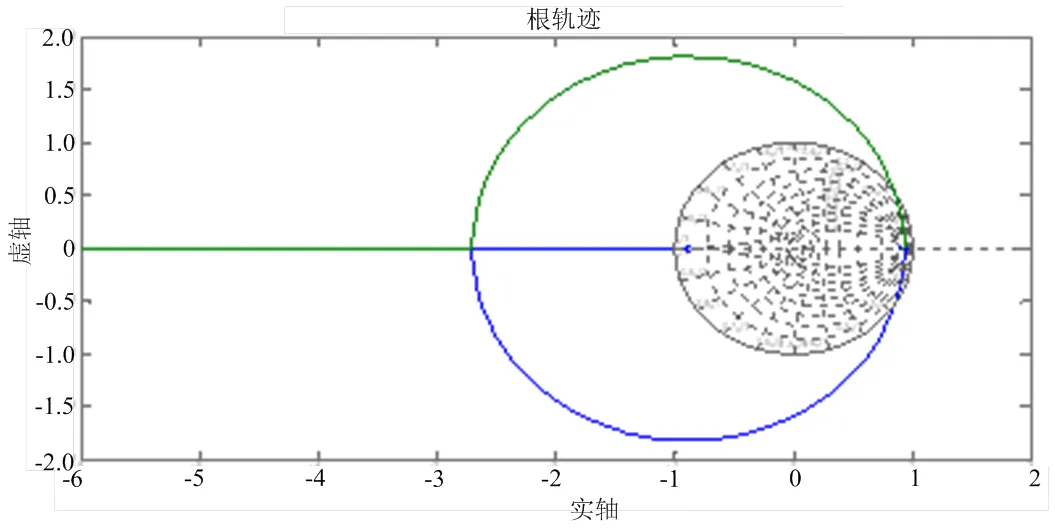
图4 纯比例调节时的根轨迹图

图5 pole变化时的根轨迹图

图6 控制系统方框图

根据性能指标要求，选取适当的，在不同极点处的响应如图6所示。从图6可以看出，值不同时，有不同的响应，在=0.1146时性能最好，此时T= 0.016 s，=1.9，满足指标要求。由于s域内的超调、调节时间都可以转化为z域的极点要求，因而可以看出，并不是越小越好，而是有一定的限制范围，超出范围，会引起超调增加，响应变慢等问题。

图7 pole变化时的响应

以上研究了根轨迹法在传递函数的应用，通过直流伺服电机转速控制的例子可以发现，应用于传递函数时，根轨迹法简单、有效，且易于实现，但是需要凭借经验进行多次的“试凑”。

图8 极点变化时响应的局部放大图

3 根轨迹法在状态空间中的应用

由于PI、PD、PID控制自由度小于闭环极点数，不能对其进行任意配制，也就是不能很好地改善系统的动、静态性能；而且在实际情况中不可避免的存在扰动作用，致使系统稳态时不能理想地跟踪参考输入而产生误差，因而在实际情况中，对状态方程下可以采取偏差积分的方式[3]。也称为状态增广系统数字控制。

在此基础上，则可以引入偏差量的积分

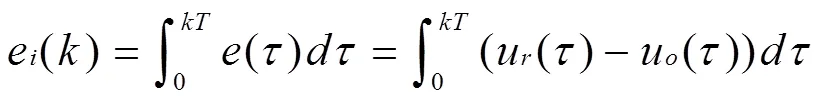
由此，可获得直流伺服电机状态空间方程为：

输出状态方程为：

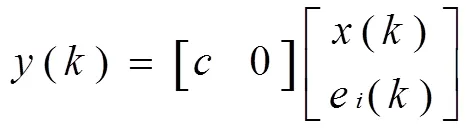
在满足(8)的条件时，此系统完全能控，因而就可以用状态反馈实现闭环极点的任意配制，就可以保障系统的稳定性、动态性能以及减小稳态误差。

¹π/(k=1,2……) (8)

由于可以用状态反馈实现闭环极点的任意配制，首先，假设反馈增益矩阵为，则直流伺服电机偏差积分状态反馈控制系统方框为图9。

将反馈增益矩阵带入(6)式，可得：

闭环系统特征方程为：

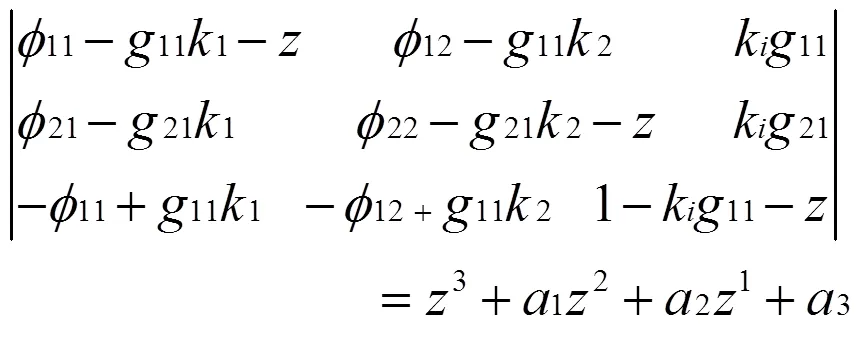
如果希望的闭环极点确定的特征方程为：

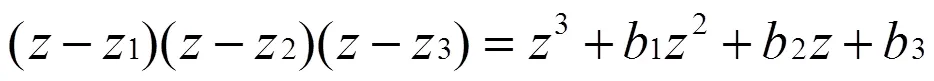
结合(10)和(11)，可以求得反馈增益矩阵。在同样的要求下，可以设置如下参数：=0.8，=5000，=10，采样周期=50ms，计算求得1=3.0660*10^6，2=0.0003*10^6，k=0.4324*10^6。图9和图10显示了直流伺服电机对指令跟踪，给定为单位阶跃信号，在=0.08 s、=0.12 s时候突加、突减负载。从图10可以看出，T=0.01 s，=2.1，仿真波形表示此控制效果很好，满足性能要求。更重要的是，此种设计方法对负载电流也有很好的抑制效果。

图9 直流伺服电机积分状态反馈控制系统方框图

图10 直流伺服电机动态指令跟踪

以上研究了根轨迹在状态方程中的应用，可以发现，在保持系统完全能控的前提下，可以通过反馈增益矩阵的合理选择将极点配置在满足性能指标的位置上，建立了量化关系，设计过程概念清晰，简洁明了，控制性能比前面需要依靠经验的效果好。但是，此种方法计算比较复杂，且在状态变量不能直接测量的情况下需要构造状态观测器，对处理器等电力电子器件的要求比较高。

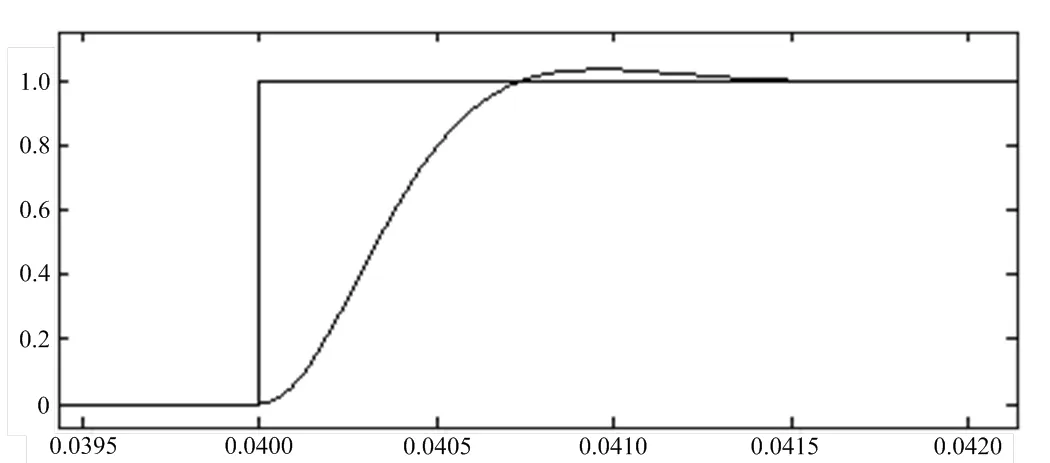
图11 直流伺服电机动态指令跟踪局部放大图

4 总结

本文介绍了根轨迹在传递函数和状态空间这两种描述方法下的具体应用。在应用于传递函数时，需要不断对系统的根轨迹进行改进，超前、滞后等校正器的零极点特别是极点对数字控制输出性能的影响很大，这种方法比较依赖经验，但是此种方法且易于工程实践。在应用于状态空间时，通过增益反馈矩阵可以与性能指标建立量化关系，对负载扰动有很好的抑制作用，设计过程概念清晰，简洁明了，控制性能也比较好；缺点就是计算比较复杂，且有可能需要构造状态观测器，对器件的要求比较高。实际工程中，要综合各方面因素综合考虑确定数字控制方案。

[1] 陈伯时. 电力拖动自动控制系统(第二版. 北京: 机械工业出版社, 1992.

[2] 杨国安. 数字控制系统-分析设计及其实现[M]. 陕西: 西安交通大学出版社, 2008.

[3] 彭力. 基于状态空间理论的PWM你变电源控制技术研究. [D]. 武汉: 华中科技大学图书馆, 2004.

Research on Application of Root Locus Method in Digital Control System

Han Wei

(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)

.

TP13

A

1003-4862（2018）12-0040-04

2018-09-12

韩巍(1977-)，男，本科。研究方向：电机控制。E-mail: 13667228872@163.com