计及风速与线路故障率周期时变特性的风电并网系统可靠性评估

2019-01-17，，

四川电力技术 2018年5期

，，

(1.贵阳职业技术学院，贵州贵阳 550081；2．国网甘肃省电力公司经济技术研究院，甘肃兰州 730050；3. 重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044)

0 引言

随着电力系统的不断发展，其运行可靠性受气象因素的影响也越来越大。在发电侧，随着全球范围内的能源危机问题日益严峻，新能源发电技术得到了迅速发展。风力发电以其清洁、可再生、建设周期短、技术较为成熟等特点在新能源发电中占据了重要地位。由于风电具有明显的随机性、间歇性特点，大规模的风电接入电网势必会影响电网的运行可靠性；在输电侧，随着电压等级不断提高，架空输电线路的跨度也越来越大，且其长期暴露在大气环境中，极易受雷电、大风、沙尘、冰雪等气象灾害的影响导致故障停运，从而影响电网的运行可靠性。

气象领域的研究指出：气候系统的演变过程具有自记忆特性，在不同的时间标度上有相似的统计特性，即大气环境具有时间周期性[1]。因此，在气象因素影响下的电网可靠性也应是随时间变化的，评估电网的时变可靠性对系统规划、中长期调度和月发电计划制定等具有重要意义。

在研究气象因素导致风力发电随机性对电网可靠性的影响时，因为风电机组出力与风速直接相关，所以目前许多文献对风速预测模型进行了研究。现有的风速模型主要有：机器学习模型、时间序列模型和概率分布模型[2]。文献[3-6]采用了各种机器学习方法及智能算法对风速进行短期预测。机器学习方法能考虑多种变量对风速的影响，预测精度较高，但模型复杂，计算量大。风速的时间序列模型通常适用于风速的中短期预测，文献[7-9]在自回归动平均模型(autoregressive integrated moving average model,ARIMA)的基础上进行了改进，提高了风速预测精度，风速时间序列模型的阶数对预测精度影响较大，低阶模型建模比较容易但误差较大，高阶模型参数估计困难。风速的概率分布模型反映的是风速长期的统计规律，通常适用于长期风速预测。常用的风速概率分布模型主要有瑞利分布、威布尔分布、对数正态分布等，其中威布尔分布使用最为广泛[10]。文献[11-12]用威布尔分布对实际风速数据进行模拟，取得了较好的效果。概率分布模型较为简单，使用方便，但是精度不高，且不能反映风速的时间变化特征。在风电接入对电网可靠性的影响方面，文献[13-16]从不同角度对风电出力随机性下的电网运行可靠性进行了评估。

在研究气象因素导致线路故障对电网可靠性的影响时，现有文献的研究重点主要关注气象因素对线路可靠性模型的影响。文献[17]对一些气候因素，如每年的极大风速和冰层厚度等对输电线路可靠性的影响进行了分析，研究结果显示气候变化会显著地影响输电线路的可靠性。文献[18]对极端气候事件导致的连锁停运故障进行研究，用极端气候随机模型和连锁故障停运模拟相结合的方法对电网可靠性进行评估。文献[19]分析了气候变化对电力系统元件可靠性的影响，提出了极端天气下提高电力系统弹性的防御策略。文献[20-22]提出一种月时间尺度下的输电线路时变故障率模型来反映气象灾害影响下线路故障与时间相关的规律，并用IEEE-RTS79系统作为算例计算了系统时变的可靠性指标。

综上所述，气象因素对风力发电和输电线路运行均有较大影响，但目前同时考虑气象因素对这二者影响条件下的风电并网系统可靠性评估还很缺乏。针对这一不足，综合考虑了风电出力和输电线路故障率周期时变特性对电网的影响，建立了风速和输电线路故障率的周期时变模型。在上述模型的基础上，用蒙特卡洛模拟法对风电并网系统的时变可靠性进行评估，最后用算例进行了验证。

1 基于风速周期时变特性的风电场出力模型

从中国气象数据网的中国地面气候资料日值数据集[23]中选取了甘肃民勤气象站2011—2015年的风速数据，对不同时间尺度下的风速变化特征进行了分析。根据整理的风速数据，绘制出2011—2015年日平均风速的时序图，如图1所示。

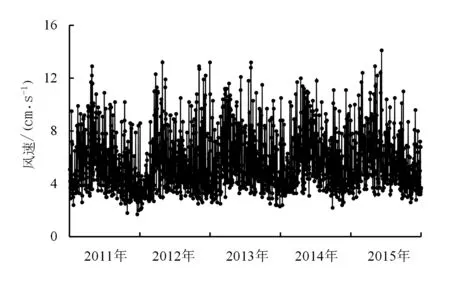
图1 民勤气象站2011—2015年日平均风速

将时间按年进行划分后可以看出，每一年风速的变化规律是相似的，即风速以年为时间尺度时表现出周期性。因此，可用累年均值分析风速在一年内的变化规律。以天为单位将累年日平均风速按时间顺序进行排列，将累年月平均风速用光滑曲线连接起来表示其变化趋势，二者绘制在一幅图上，如图2所示。

图2 2011—2015年累年日平均风速及月变化趋势

可见，风速以年为时间尺度时主要表现出周期特征，以月为时间尺度时表现出全年随时间的主要变化趋势，以日为时间尺度时在月变化趋势附近表现出波动特征。这里将风速的这种多时间尺度变化规律概括为风速的周期时变特性。

1.1 风速的周期时变特性建模

由上述分析可知，同一地区每一年风速的变化规律是相似的。因此，其周期特征可以通过累年均值来反映。以累年月平均数据为样本，用拟合函数f(t)表示其变化趋势；用累年日平均风速和拟合函数值作差得到波动量，用服从某一概率分布的随机变量ε(v)模拟其波动特征。最后将拟合函数与随机变量相叠加得到风速的周期时变模型F(t)。

采用曲线拟合法根据具体的风速样本建立不同地区的风速周期时变模型。用拟合优度确定拟合函数形式及概率分布类型，用最小二乘法确定模型中的待定参数值。曲线拟合法是在建模过程中一种常用的数据处理方法。其思路是，用某种方法寻找一条光滑曲线使其尽量逼近样本数据。比较常用的曲线拟合方法是最小二乘法。

最小二乘法曲线拟合的原理是：对于一组已知的数据集合{(xi，yi)}(i=0，1，2，…，n)，构建一个函数g(a，x)，其中a为待定的参数向量，通过使误差平方和SE最小来确定函数g(a，x)中的未知参数，计算误差平方和的公式如式(1)。

SE=∑(g(a,xi)-yi)2

(1)

式中函数g(a，x)称为拟合函数或最小二乘解。使用Matlab软件中的曲线拟合工具箱来实现曲线拟合，计算拟合优度和确定拟合模型中的参数值。

下面以民勤气象站2011—2015年的风速样本为基础，详细介绍风速周期时变模型的建立过程。

1.1.1 风速月变化趋势拟合

首先对风速的月变化趋势进行曲线拟合，以累年月平均风速作为纵坐标，以每月天数的中位数作为横坐标，得到图3中的散点。使用Matlab曲线拟合工具箱中的傅里叶函数和高斯函数进行拟合，拟合优度中R2为可决系数，越接近于1拟合效果越好；RMSE为均方根误差，越接近于0拟合效果越好。拟合优度如表1所示。

表1 风速月变化趋势拟合函数拟合优度

从表1可以看出，二阶傅里叶函数与三阶傅里叶函数的拟合优度接近，但三阶傅里叶函数表达式更为复杂，待定参数更多，因此为了降低复杂度，这里选择二阶傅里叶函数作为拟合函数，其函数表达式为

f(t)=a0+a1cos(ωt)+b1sin(ωt)+

a2cos(2ωt)+b2sin(2ωt)

(2)

用最小二乘法可计算出拟合函数中的待定参数值，如表2所示。

表2 风速月变化趋势拟合函数中待定参数的拟合值

确定参数值后可绘制出拟合曲线，将其与累年月平均风速比较，如图3所示，从图中可以看出采用二阶傅里叶拟合函数能较好地反映风速的月变化趋势。

图3 风速月平均风速及拟合曲线

1.1.2 风速波动分量拟合

风速的波动分量是累年日平均风速与拟合函数值的差值，表达式为

Δv(t)=v0(t)-f(t)

(3)

式中：Δv(t)是第t天风速的波动分量；v0(t)是风速在第t天的累年日均值；f(t)是第t天的拟合函数值。

根据上述的风速样本及拟合函数值计算出的Δv(t)在零值附近来回波动，具有随机性，可看作是服从某一概率分布的随机变量ε(v)，与时间无关。绘制Δv(t)的频率直方图，此直方图的矩形顶边接近一光滑曲线，该曲线就是随机变量ε(v)服从的概率密度函数曲线。同样地，运用曲线拟合的方法可确定风速波动分量的概率分布模型及其参数。随机变量ε(v)有正有负，因此应选取横坐标能取到负值的概率密度函数。下面分别选取了正态分布、三参数伽马分布及三参数威布尔分布对其进行拟合，拟合优度如表3所示。

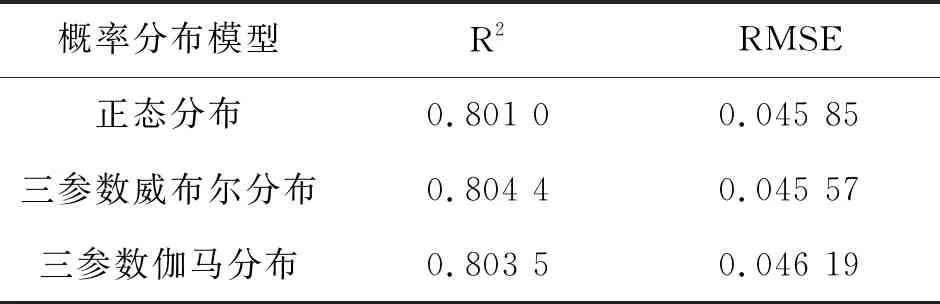
表3 风速波动分量概率分布拟合优度

拟合优度的结果显示三参数威布尔的拟合效果较好，因此选择三参数威布尔分布作为风速波动分量的概率分布模型，其概率密度函数为

(4)

式中：α为尺度参数；β为形状参数；γ为位置参数。用最小二乘法确定参数值，如表4所示。

表4 风速波动分量概率分布拟合中待定参数的拟合值

确定参数值后可求解出对应的三参数威布尔分布概率密度函数，风速波动分量的频率直方图及概率密度函数拟合曲线如图4所示。可以看出三参数威布尔分布较好地体现了风速波动分量的概率分布特征。

1.1.3 风速的周期时变模型

所举例中风速的月变化趋势用二阶傅里叶拟合函数f(t)来表示，波动分量用服从三参数威布尔分布的随机变量ε(v)来表示，风速的周期时变模型为二者的叠加，表达式为

图4 风速波动分量频率直方图及概率密度拟合曲线

(5)

式中，F(t)为风速周期时变模型在第t天的模拟值。

实际风速值与模型模拟值的比较如图5所示，可以看出二者能较好地吻合。

图5 累年日平均风速与模型模拟值

1.2 计及风速周期时变特性的风电场出力模型

气象站的标准观测高度距地面10 m，因此在计算风机出力时需将风速换算到风机轮毂高度。根据GB/T 18710-2002《风电场风能资源评估方法》[24]，对不同高度的风速进行换算，公式为

(6)

式中：a为风切变指数；v2为高度z2的风速；v1为高度z1的风速。风切变指数可用式(7)计算：

(7)

式中，v1、v2分别为高度z1、z2下风速的实测值。若没有不同高度的实测风速数据，风切变指数a可取0.143作为近似值。

通过风机出力与风速之间的函数关系[25]，可得到风电场的出力模型，其函数表达式如下：

(8)

式中：Pt为第t天的风电场出力，Pr为风电场装机容量，MW；Vt为第t天的风速；Vci、Vr、Vco分别表示风机的切入风速、额定风速和切除风速，m/s；中间变量A、B和C可由以下公式表达：

(9)

(10)

(11)

将由风速的周期时变模型F(t)模拟生成的时变风速作为变量Vt代入式(8)中，可得风电场出力的周期时变模型Pt。

2 输电线路故障率的周期时变模型

随着电压等级不断提高，架空输电线路的跨度也越来越大，且其长期暴露在大气环境中，极易受雷电、大风、沙尘、冰雪等气象灾害的影响。文献[26-27]指出气象灾害是造成架空输电线路故障停运的主要原因。目前电力系统可靠性评估中线路故障率常采用多年统计得到的年均值进行计算，而实际上由于气象灾害具有明显的时空分布特征，因此受其影响，输电线路的故障率也是随时间、空间变化的。下面借鉴文献[20]的研究思路和研究方法，建立了输电线路周期时变模型。

2.1 历史同期故障率统计

与风速类似，从年时间尺度来看气象灾害也具有周期性，例如中国每年的1—2月易发生冰雪灾害，每年的7—8月雷电灾害频发，由气象导致的线路故障频率也随之变化。因此，基于多年的气象灾害导致线路故障的记录，按月进行统计，可计算得到线路各月的历史同期故障率。

单条输电线路历史同期月故障率可以表示为

(12)

式中：λk(m)表示线路k在历史同期的第m月的故障率，次/(100 km月)；nkym为线路k在第y年的m月的故障次数；Tm表示第m月的时间；Y为统计的总年数；Lk表示线路k的长度，km。

式(12)可推广到计算相似气象条件下某一地区多条线路的历史同期各月故障率，公式为

(13)

式中，λ(m)表示同一电压等级线路在历史同期的第m月的故障率，次/(100 km月)。

根据甘肃电网2014—2016年330 kV输电线路故障记录进行统计，用式(12)、式(13)计算出甘肃地区输电线路的历史同期各月故障率，并与年均值故障率进行比较，如图6所示。

图6 甘肃地区线路历史同期各月故障率与年均值故障率

2.2 输电线路周期时变故障率模拟

基于上面得到的历史同期故障率，可进一步用曲线拟合的方法模拟其变化规律，用拟合函数H(t)来建立输电线路故障率的周期时变模型。

以图6中甘肃地区线路的历史同期各月故障率为样本，用不同阶数的傅里叶函数和高斯函数对其进行曲线拟合，其拟合优度如表5所示。

表5 甘肃地区线路历史同期各月故障率拟合优度

从表5中可以看出，用三阶傅里叶函数对两地区的故障率进行拟合均能取得较好的拟合效果，因此选用三阶傅里叶函数作为拟合函数，其函数表达式为

f(t)=a0+a1cos(ωt)+b1sin(ωt)+a2cos(2ωt)+

b2sin(2ωt)+a3cos(3ωt)+b3sin(3ωt)

(14)

用最小二乘法计算出拟合函数中的待定参数，如表6所示。

确定参数值后可绘制出对应的拟合曲线，历史同期故障率及拟合曲线如图7所示。

表6 线路故障率拟合函数中待定参数的拟合值

图7 甘肃地区线路历史同期各月故障率及拟合曲线

从图7中可以看出拟合曲线与历史同期故障率是基本吻合的，且根据表5可知三阶傅里叶函数的拟合精度较高，说明该拟合函数能较好地反映故障率的时变特征。

3 风电并网系统可靠性评估方法

将前面建立的风速和输电线路故障率的周期时变模型运用到传统的电力系统可靠性评估中，得到了综合考虑气象因素对风电出力及输电线路故障率影响下的风电并网系统时变可靠性评估方法。

3.1 评估指标

根据所建立的风速周期时变模型，可在发电侧模拟风电场出力的随机性、季节性等特征；根据所建立的输电线路故障率的周期时变模型，可在输电侧模拟气象灾害影响下的线路故障率的时变特征。将二者结合起来，运用蒙特卡洛模拟法，可计算风电并网系统的时变可靠性，将系统各月的失负荷概率(loss of load probability,LOLP)和电力不足期望(expected domand not supplied,EDNS)作为可靠性指标对风电并网系统的时变可靠性进行评估。

3.2 评估流程

基于风速和输电线路故障率周期时变模型的风电并网系统时变可靠性评估的流程如图8所示。

用蒙特卡洛模拟法对风速周期时变模型进行抽样时，由于模型中有一部分是随机变量ε(v)，因此每次抽样首先需要生成服从拟合得到的概率分布的随机数，再与f(t)叠加得到第i次抽样的风速模拟值Fi(t)。然后根据考察的时间区间产生[t1,t2]之间均匀分布的随机正整数ti，其中t1、t2分别为抽取时间区间的上、下限。例如在计算系统一月份的可靠性指标时ti∈[1,31]，抽取的风速表达式为

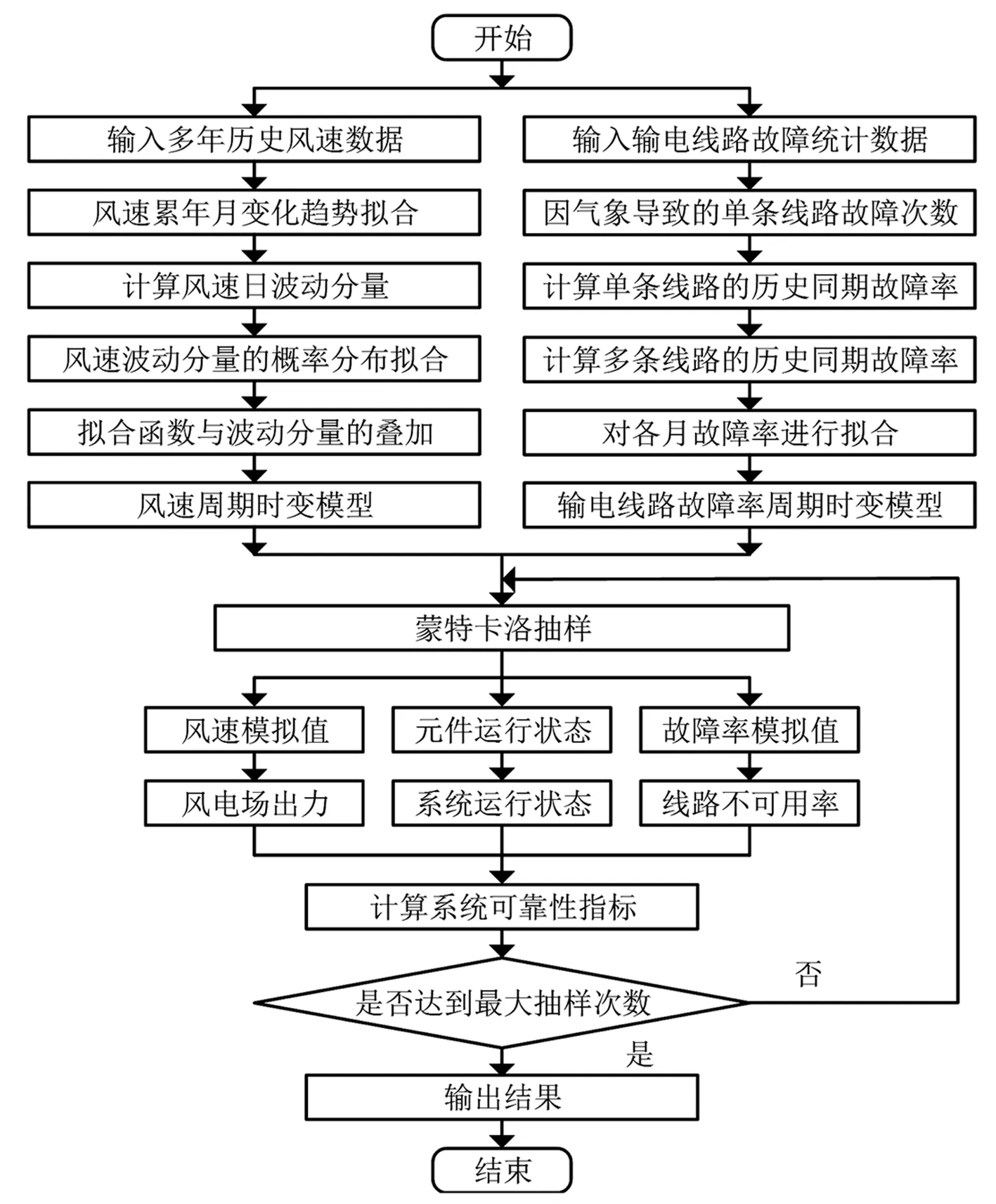
图8 基于风速和线路故障率周期时变模型的风电并网系统可靠性评估流程

vi=Fi(ti),ti∈t1,t2

(15)

式中：vi为第i次抽取的风速值；Fi(ti)为第i次抽样的风速周期时变模型生成的第ti天的风速模拟值。进一步由式(8)可计算出风电场的出力。各月ti所对应的抽样时间区间如表7所示。

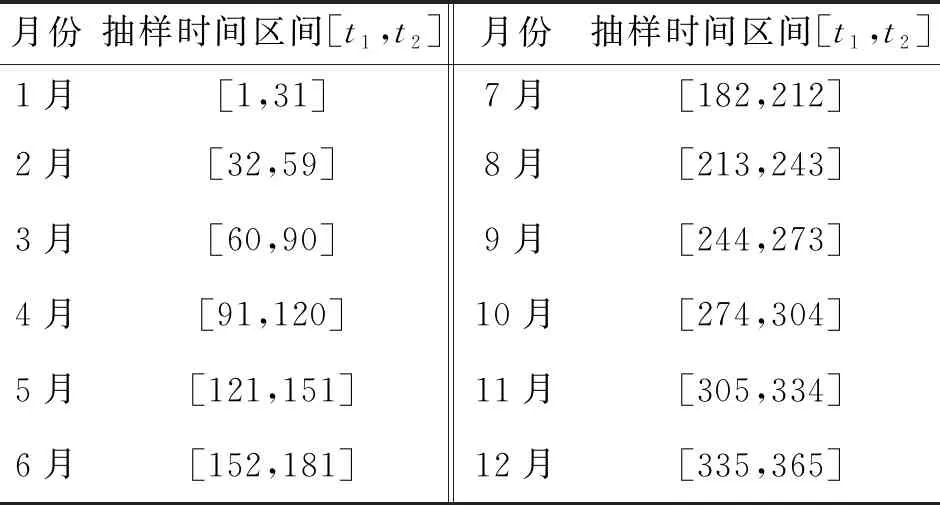
表7 各月ti对应的抽样区间

输电线路采用两状态模型，即正常运行状态和故障停运状态，其不可用率的表达式为

(16)

式中：U为线路的不可用率；λ为故障率；μ修复率。在所提出的风电并网系统可靠性评估中，关注的是月时间尺度的可靠性指标，因此λ采用所提出的输电线路故障率周期时变模型，而μ基本上与时间无关，因此可取多年统计值进行计算。

用蒙特卡洛模拟法对系统中各元件的运行状态进行抽样时，用产生随机数的方法来模拟各个元件的状态，通常是产生[0,1]之间均匀分布的随机数Rj，每个元件的状态由式(17)确定：

(17)

式中：0表示正常工作状态；1表示故障停运状态；Uj是第j个元件的不可用率。

按上述方法多次对某月的风电场出力、线路故障率和系统中各元件状态进行抽取，可模拟系统各种运行状态，进而计算得到系统在该月的失负荷概率(LOLP)和各月的电力不足期望(EDNS)。

4 算例分析

按照前述方法建立了甘肃瓜州、马鬃山、玉门、民勤、环县等5个风电集中地区的风速周期时变模型和甘肃地区的输电线路故障率周期时变模型。根据图8所示的可靠性评估流程，用Matlab软件进行编程，以改造的IEEE-RTS79系统为算例，对其时变可靠性进行了评估。

原IEEE-RTS79系统中不含风电机组，现分别将节点22、15、13、1和7处的1台50 MW、12 MW、197 MW、20 MW和100 MW的发电机组替换为等装机容量的风电场，系统的结构及各元件参数见文献[28]，算例中的负荷采用系统各月的峰值负荷，如图9所示。

图9 IEEE-RTS79系统各月峰值负荷

算例对Case 1和Case 2两种情形下系统各月的失负荷概率和电力不足期望指标进行了计算。两种情形下所采用的风速模型和线路故障率模型如表8所示。

表8 Case 1和Case 2的计算条件说明

计算所得结果如图10和图11所示。

图10 Case 1和Case 2情形下系统各月的LOLP

图11 Case 1和Case 2情形下系统各月的EDNS

系统可靠性指标中失负荷概率LOLP和电力不足期望EDNS越大，说明系统可靠性越低；反之，系统可靠性越高。目前风电并网系统可靠性评估多采用Case 1的计算条件，即风速模型采用威布尔分布，线路故障率模型采用年均值故障率。但威布尔分布本质上是一种概率分布模型，不具备时间属性，并且年均值故障率也无法反映其各月的差异，因此采用上述条件计算得到的系统各月可靠性指标并不能真实反映系统可靠性随时间的变化情况。从图10和图11中可以看出，Case 1所得结果比Case 2偏低，即采用传统方法评估风电并网系统各月可靠性时，可能会造成对可靠性的低估。这是因为，相比于Case 1，Case 2的计算条件充分考虑了气象因素导致的风电出力和线路故障率周期时变特性对电网的影响，更加接近实际。

利用所提方法能真实反映系统可靠性随时间的变化情况，使系统运行人员提前对系统各月的可靠性水平有所把握，事先制定好相应的降风险措施。例如，在运行方面，加强气象灾害多发时段相关线路的巡检工作；检修方面，事先制定好高风险时段的应急措施并准备好事故抢险物资；调度方面，在制定月发电计划时，可在系统可靠性较低月份限制部分风电场的出力，以减小风电出力随机性对电网的影响，同时加大部分火电机组的出力以保证供电。