Simulation of vehicle braking behavior on wet asphalt pavement based on tire hydroplaning and frictional energy dissipation

Liu Xiuyu Cao Qingqing Chen Jiaying Huang Xiaoming

(School of Transportation, Southeast University, Nanjing 210096, China)

Abstract：To investigate the influence of wet conditions on vehicle braking behavior, a numerical-analytical method was proposed for the simulation of tire hydroplaning and frictional energy dissipation. First, a finite element model of tire hydroplaning was established using the coupled Eulerian-Lagrangian method, including a pneumatic tire model and a textured asphalt pavement model. Then, the frictional force on the tire-pavement interface at different speeds was calculated by the model. Based on vehicle braking mechanism and frictional energy dissipation, a calculation method for braking distance was proposed based on a three-stage braking process. The proposed method was verified by comparing the calculated hydroplaning speed and braking distance with field test results. Then, vehicle braking distances and wet friction coefficients were calculated under different conditions. The results show that thinner water film, a more complex tread pattern and higher tire inflation pressure all contribute to the vehicle braking performance; moreover, the pavement texture has obvious influence on vehicle braking behavior, especially at a high speed. The proposed method shows great effectiveness in predicting vehicle braking behavior on wet asphalt pavements.

Key words：tire hydroplaning; vehicle braking distance; coupled Eulerian-Lagrangian method; water film; tire inflation pressure; tread pattern; pavement texture

Low skid resistance of wet pavement has been recognized as a key contribution to highway accidents. When a tire rolls on asphalt pavement covered with a water film, water acts as a lubricant on the tire-pavement interface and provides a hazardous hydrodynamic force. Due to the deterioration of tire-pavement adhesion, the braking and cornering capability of the vehicle declines dramatically. When the vehicle speed increases to a critical value, the hydrodynamic force can uplift the tire and cause some unpredictable situations. This phenomenon is called hydroplaning and the critical value is hydroplaning speed.

The increasing demand for driving safety poses challenges to highway authorities and it is required to evaluate pavement conditions precisely under rainy conditions. Numerous field tests, theoretical calculations and numerical simulations were carried out in this field. A classical empirical formula that describes the relationship between the hydroplaning speed and the tire inflation pressure was obtained through field tests on smooth tire hydroplaning by NASA[1]. After that, by a series of field tests, Horne et al.[2-3]modified and improved the formula considering tire type, water film thickness and pavement texture. However, experimental research has a limited scope of reusability due to high risk and high cost. To overcome this drawback, an elastohydrodynamic lubrication theory was introduced to calculate the hydroplaning speed[4], which was effective in determining the hydrodynamic force on the tire, but it only considered a two-dimensional tire footprint region and ignored the dynamic vibration on the tire-pavement interface. Furthermore, Fwa et al.[5-7]proposed a numerical method to simulate the three-dimensional tire hydroplaning, and they established a skid resistance model for grooved pavements. Although the asphalt pavement was simulated simply by an analytical surface, they succeeded in relating tire hydroplaning speed to climate conditions and tire characteristics.

However,hydroplaning speed is not a good indicator of transportation safety since it is not closely related to real driving conditions on rainy days. In fact, drivers are usually cautious, and the vehicle speed can hardly reach tire hydroplaning speed. In this situation, traffic accidents occur mainly due to the decrease in the vehicle braking distance. Thus, vehicle braking distance, rather than hydroplaning speed, is an important indicator of vehicle driving safety on wet asphalt pavement. As a result, it is of high significance to predict vehicle braking distance on rainy days without a need for a field test.

In this paper, a hydroplaning model incorporating textured asphalt pavement and pneumatic tire was constructed in ABAQUS. Based on the numerical-analytical analysis of the vehicle braking process, asphalt pavement skid resistance on wet conditions was evaluated using the vehicle braking distance and wet friction coefficient. Evaluation was performed on the influence of tire tread pattern, tire inflation pressure, water film thickness and pavement texture.

1 Finite Element Modeling of Tire-Pavement Hydroplaning

1.1 Modeling of tire, pavement and water film

Tire hydroplaning occurs when tires roll on the wet asphalt pavement at high speed. Dynamic hydroplaning and viscous hydroplaning contribute together to the reduction of pavement skid resistance. Dynamic hydroplaning dominates the hydroplaning process when the water film thickness is less than 0.25 mm, and viscous hydroplaning is notable when the water film is thick enough to provide a strong lifting force. In these two phenomena, tire type, pavement texture and water viscosity are the primary factors influencing tire hydroplaning[8-10]. To ensure the accuracy of the proposed method, all these factors should be considered when establishing a tire hydroplaning FE model.

Fig.1 shows the 2D geometric cross-section of a 175-70-R15 pneumatic tire. After the tire cross section was drawn and meshed, material property was assigned to corresponding sections. Then, the 2D cross section was rotated and attached to a pattern component to form a partial 3D tire model. Finally, the full-scale patterned tire was obtained by rotating the partial 3D tire model. Drainage channel on tire-pavement interface is significant in improving tire hydroplaning performance. Thus, the tire tread pattern combining transverse grooves and longitudinal grooves were added to the tire surface in this model.

Fig.1 Generation of a three-dimensional tire model (unit: mm)

In the proposed FE model, a tire was simulated as a composite structure containing rubber and reinforcement. The hyperelastic mechanical behavior of rubber was described by the YEOH model. Reinforcement of belts, ply, inner linear and bead were simulated as embedded rebar elements with specific angles, gaps and section areas. Detailed modelling information can be found in previous research[9].

One highlight of this research is the construction of an asphalt pavement model with an authentic macro texture. In previous research[11], similar work was conducted by computed tomography (CT) scanning technology and reverse reconstruction technology, which requires tedious meshing work and consumes huge computational resources. As an improvement, a three-dimensional optical scanner was used in this research to acquire the morphology of the prepared slab specimens. In the reconstruction process, two cameras in the scanner worked together to obtain the coordinate data of the specimen surface. After the surface containing these points was visualized and meshed, a textured asphalt pavement model was established through smoothing, extending and mirroring. The procedures of the scanning and the setup are shown in Fig.2. In this proposed modelling method, the measurement accuracy of 5 μm was effective in reflecting actual asphalt pavement texture. The mean profile depth (MPD) values of the five slab specimens used in the research were 0.33, 0.45, 0.65, 0.74 and 0.85 mm.

(a)

(b)

(c)

Fig.2Generation of a textured pavement model.
(a) 3D optical scanning; (b) Scanned surface information; (c) Textured pavement model

Considering the influence of the tread pattern and pavement texture on hydroplaning, the mesh size of the water film model was limited to fill the space in the tread pattern and pavement texture. Thus, an air-water composite model with a water inlet and outlet was required to avoid the tedious modelling process and to reduce computing time. With a size of 320 mm×390 mm×80 mm, the model allows water spraying to the maximum height of 80 mm. Instead of the tire rolling on a full-scale pavement model covered with water film, water flowed and rushed the tire model at a high speed. The Mie-Grüneisen equation[12]is used to describe the state of the water film under the influence of the tire, which is given as

wherepis the water pressure;Γ0is the material constant;η=1-ρ0/ρ;ρ0is the water initial density;ρis the water density under impact;Emis the specific internal energy of water.

The material parameters[11]in the Mie-Grüneisen equation can be determined based on the experimental data of water. In this paper,ρ0=998.203 kg/m3,c0=1 480 m/s,s=1.92, andΓ0=1.2. Meanwhile, the linear viscous shear behavior for water was described as Newtonian fluid. The kinematic viscosity and temperature are set to be 1.006×10-6m2/s and 20 ℃, respectively.

1.2 Model assembly and implement

The tire model and water film model are composed of Euler elements and Lagrange elements, respectively. The coupled Eulerian-Lagrangian (CEL) method[13]was used to solve the fluid-structure interaction problem when the tire rolled on the wet asphalt pavement at a high speed. In this method, Lagrange meshes of tire were overlapped by empty meshes in Eulerian elements, indicating that the tire was immerged in part of the empty meshes. This process facilitated the loading of the surface fluid pressure on the tire contact area by tracking the motion of free fluid surface in the calculation process. At the same time, the volume fraction and speed boundary condition were updated according to the renewal of the tire node displacements and speeds on the interaction surface using the volume of fluid (VOF) method[14].

After the tire-asphalt pavement hydroplaning FE model was established, an implicit and explicit analysis was conducted to achieve hydroplaning simulation. In the implicit analysis, uniformly-distributed load was applied on the inner surface of the tire model as the initial tire inflation pressure. Then, a quarter of the vehicle weight was loaded in the vertical direction to represent vehicle load. In the explicit analysis, the angular velocityωwas specified for the tire model. The equivalent linear speedvwas specified for the asphalt pavement model and the water flow through the inlet. The simulation conditions are shown in Fig.3.

Fig.3 Hydroplaning model of tire-asphalt pavement

1.3 Acquisition of tire-asphalt pavement interactive force

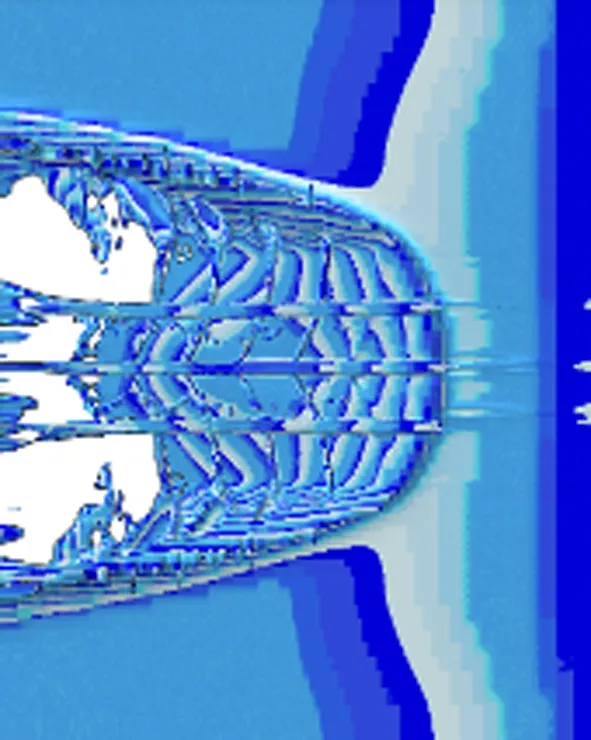
The simulation based on the proposed tire hydroplaning model was carried out with the vehicle speed increasing from 0 km/h until the tire was fully lifted by the water flow. The water film thickness and slip ratio are set to be 10 mm and 15%, respectively. Other model parameters are shown in Tab.1. In this process, water film trace on the tire-pavement interface is recorded, and the result is displayed in Fig.4. With the increase of vehicle speedV, the tire-pavement contact area decreases, and the water covered area increases. Meanwhile, the influence sphere of tire on the water surface is reduced.

Tab.1 Model parameters for tire hydroplaning analysis

At the same time, the vertical force provided by the pavement and water in tire hydroplaning was recorded. The result is presented in Fig.5. In the partial hydroplaning process, the tire-pavement contact force increased and water lifting force decreased. When the vehicle speed reached 79.2 km/h, the water lifting force achieved its maximum value and the tire-pavement contact force reduced to 0 N. At this moment, the pavement provided no holding power, which consequently caused the tire hydroplaning phenomenon. The consistency between the water film trace and tire-pavement-water interaction force at different vehicle speeds is confirmed by the results in Fig.4 and Fig.5.

(a) (b) (c)

(d) (e) (f)

Fig.4Recorded water film trace at tire-pavement interface.
(a)V=20 km/h; (b)V=30 km/h; (c)V=40 km/h; (d)V=60 km/h; (e)V=70 km/h; (f)V=80 km/h

Fig.5 Tire-pavement-water interaction vertical force

Then, tire hydroplaning was simulated with the vehicle speed increasing from 0 km/h until tire hydroplaning occured with the water film of 0.5, 2, 5 and 10 mm, respectively. In this process, the water lifting force and longitudinal force on the tire were measured. When water lifting forces reached their maximum values, the critical hydroplaning speeds for the proposed model under different water film thicknesses were 126.6, 103.2, 89.2 and 79.6 km/h, respectively. The longitudinal force on tire contains pavement friction force and water drag force, both contributing to the tire frictional energy dissipation. The recorded data of the tire-pavement interaction force in the hydroplaning process was used in the following analysis.

2 Vehicle Braking Distance Calculation with ABS Locked

2.1 Braking mechanism of ABS locked vehicle

When a vehicle brakes on the asphalt pavement, tire moves gradually from a free rolling status to a locked status. The vehicle speedV, tire angular velocityω, and tire rolling radiusrare used to specify the motion condition of the tire(see Fig.6(a)). The slip ratioSis used to evaluate the slipping proportion in tire braking process[15],

Fig.6(b) shows the variation of the friction coefficient on tire-pavement interface. The friction coefficient started to increase when slip proportion increased from a free rolling status. After the coefficient achieved its maximum value at a slip ratio of about 17%, the coefficient started to decrease. Thus, the slip ratio must be controlled within the range of 15% to 20% to obtain a maximum tire-pavement friction force. This range of slip ratio control is used by the anti-locked braking system (ABS) to achieve the shortest braking distance.

(a)

(b)Fig.6 Tire slip ratio during vehicle braking. (a) Force and moving conditions of the tire; (b) Longitudinal frictional responses with slip ratio

In Fig.6(a), the relationship between friction forceFand braking torqueTis given as

whereMandItare the total vehicle mass and the moment of inertia of a tire, respectively.

When the slip ratio is defined, the braking torque can be determined by the prescribed friction force as

Based on the dynamic equilibrium of a patterned tire, the variation of the braking torque with vehicle speed can be derived from the calculated tire friction force. Then, the ABS braking process was simplified into three stages[16]: 1) In a short time(0.25 s) after the driver pushes the brake pedal, the disc pressure increases linearly to slow down the tire angular velocity. 2)Then, the disc pressure is regulated smoothly to keep the tire slip ratio at a preset value(17%). 3) When the vehicle speed is smaller than a certain speed(20 km/h), ABS is removed and the tire is maintained in a fully locked condition.

2.2 Energy dissipation and calculation of braking distance

When a vehicle runs on the wet asphalt pavement, the existing energy of the vehicle is composed of translation energyEvand rotation energyEwas

Ev=MV2/2,Ew=2Iw2

When the vehicle starts to brake, the existing vehicle energy decreases due to the reduction in vehicle speed and tire angular velocity. The dissipation of vehicle energy plays the role of overcoming the frictional force and braking torque. The energy dissipation in the vehicle braking process is given as

whereEtireis the tire frictional energy dissipation;Ediscis the disc frictional energy loss;t0is the total braking time;rdis the radius of disc pad;μdis the friction coefficient between disc liner and disc pad; andAcis the section area of the wheel cylinder.

To illustrate the frictional energy loss in the vehicle braking process, Fig.7 shows the distribution of the frictional energy rate on the tire-pavement interface when vehicle brakes at the speed of 30 and 70 km/h. The distribution was obtained by the proposed tire-pavement interaction model. It is revealed that the frictional energy dissipation varies with different tire nodes and different braking speeds.

In the process of calculating braking distance and braking time, the linearly increasing stage of the slip ratio and disc pressure is first considered. The vehicle speed

(a)

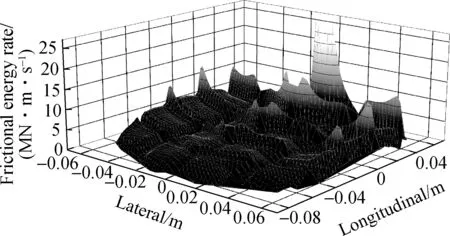
(b)Fig.7 Distributions of frictional energy rate. (a) At V=30 km/h; (b) At V=70 km/m

and travelling distance at timet=0.25 s can be calculated as

In the second stage,highly nonlinear variation of vehicle speed during braking is considered. The decline of vehicle speed fromVt=0.25toV=20 km/h is divided into numerous small braking speed intervals,Δvi=[vi-1,vi](i=1,2,…,n). Fixing the slip ratio at 17%, the time it takes to slow the vehicle speed fromvi-1toviis calculated as

Then, the braking timeT′and braking distanceD′ with the fixed slip ratio can be calculated as

In the third stage, braking timeT″and braking distanceD″ are calculated when the vehicle speed decreased fromV=20 km/h to 0, with the slip ratio fixed at 100% by the same method.

Finally, combining the results in the first two stages, the total braking time and braking distance are calculated as

T=0.25+T′+T″

D=Dt=0.25+D′+D″

When a vehicle brakes on dry road or wet road with the initial speed of 100 km/h, the vehicle speed decreases and braking distance increases with braking time. Fig.8 shows the total braking time and braking distance on a dry road of 3.4 s and 49 m, respectively. On a wet road, the

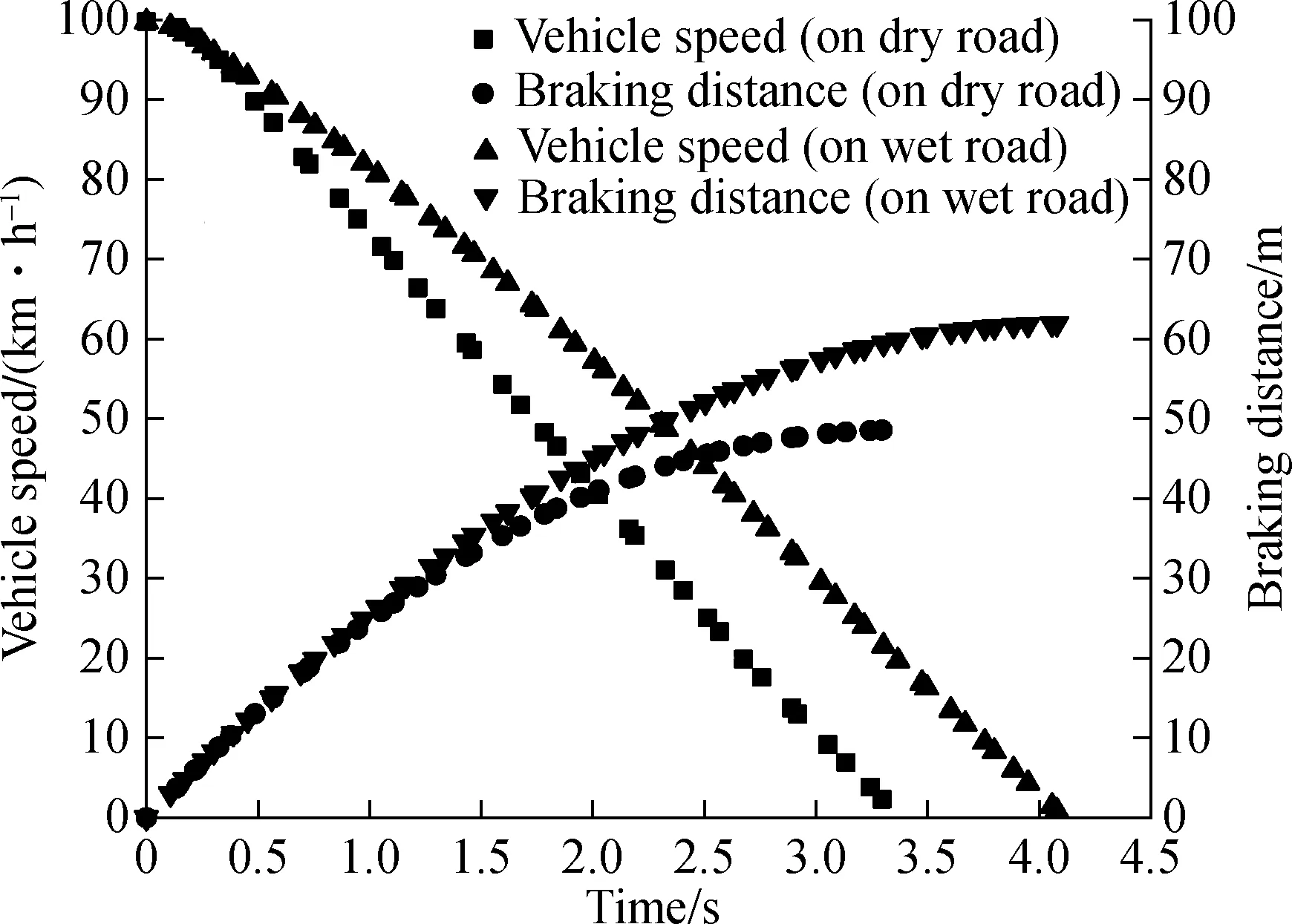
Fig.8 Vehicle speed and braking distance

total braking time and braking distance increase to 4.1 s and 62 m. Different variation tendencies of vehicle speed are observed corresponding to the three braking stages.

3 Verification of the Proposed Method

Based on the preset parameters in Tab.1, numerical simulation and calculation of the braking distance are carried out. The calculated vehicle braking distance is compared with field test data in Denmark[17](see Tab.2). In the experiment, the cars with ABS drove on dry and wet roads at the vehicle speed of 80, 110 and 130 km/h, respectively. Before that, a water truck was used to create a wet road surface with the water film thickness between 1.3 mm and 1.6 mm. The predicted vehicle braking distance data fitted well with the test results. On the asphalt pavement with the water film thickness, the predicted data were slightly higher than that of the test results. This can be explained by the existence of the cross slope and the loss of water film. In this circumstance, the controlled water film was smaller than the predicted value.

Tab.2 Comparison of calculated and measured braking distance

4 Vehicle Braking Behavior

Vehicle braking behavior is influenced by several factors related to vehicle and pavement conditions. In this section, the vehicle braking distance and wet friction coefficient are calculated and analyzed. The influence of water film thickness, tire tread pattern, tire inflation pressure and pavement texture are discussed.

4.1 Vehicle braking distance under different conditions

Water film thickness on the asphalt pavement is influenced by rainfall intensity, road slope, slope length and surface roughness. As shown in Fig.9(a), the vehicle braking distance on the asphalt pavement for the water film thickness of 0.5, 2, 5 and 10 mm is calculated. In this process, the tire model is established with the combined pattern and an inflation pressure of 240 kPa. The results indicate that the influence of water film thickness increases with the increase of initial vehicle speed. For the four-different water film thicknesses, the vehicle braking distance at 80 km/h is 37.1, 40.6, 44.1 and 50.2 m, respectively.

Three different patterns are considered when calculating the vehicle braking distance, as shown in Fig.9(b). The longitudinal pattern is simply composed of four longitudinal grooves. The combined pattern contained two longitudinal grooves and substantial lateral grooves. Compared with the former two patterns, the complex pattern consists of much more complex grooves. The observed fact that the vehicle equipped with the tire of the complex pattern stopped at the shortest distance proves the superiority of the tire tread pattern of this kind.

Tire inflation pressure is simulated by applying a uniformly-distributed load on the inner surface of the tire model. Considering the variation of tire inflation pressure in practice, the pressure is set to be from 120 to 360 kPa with an interval of 60 kPa. As is shown in Fig.9 (c), the variation of the vehicle braking distance reveals that higher tire inflation pressure can improve vehicle braking performance.

4.2 Wet friction coefficient influenced by pavement texture

In this section,the wet friction coefficient was used to evaluate the vehicle braking performance. The coupling effect of the MPD value and vehicle speed was investigated. In the simulation, the wet friction coefficient is calculated as

whereμis the wet friction coefficient;Fpis the pavement friction force;Fwis the water drag force; andFlis the vehicle load.

(a)

(b)

(c)Fig.9 Vehicle braking distance under different conditions. (a) Different water film thickness; (b) Different tire tread pattern types; (c) Different tire inflation pressures

The calculation results are shown in Fig.10. For the fixed water film thickness, tire inflation and vehicle load, the wet friction coefficient increases with the increase in the MPD value. When the vehicle speed is 20 km/h, the wet friction coefficient increases from 0.64 (MPD 0.33 mm) to 0.76 (MPD 0.85 mm). Meanwhile, when the MPD increases from 0.33 to 0.85 mm, the wet friction coefficient increases by 18.9%, 46.9%, 133.3% and 511.1%, respectively, corresponding to the vehicle speed

Fig.10 Wet friction coefficient influenced by pavement texture

of 20, 40, 60 and 80 km/h, respectively. It can be concluded that the influence of pavement texture becomes more obvious when the vehicle speed increases.

5 Conclusions

1) The consistency between water film trace and tire-pavement-water interaction force at different vehicle speeds is confirmed. Compared with the measured data in Denmark, the proposed method is verified to be accurate in predicting vehicle braking distance on a wet pavement.

2) Vehicle braking distance is greatly influenced by water film thickness. When the water film grows thicker, the pavement frictional force on tire decreases and the water drag force increases. For a water film thickness of 0.5, 2, 5 and 10 mm, the braking distances at 80 km/h are 37.1, 40.6, 44.1 and 50.2 m, respectively.

3) The tire tread pattern provides drainage channels for the water film and improves vehicle braking performance.The vehicle braking distance with different tire patterns, including the longitudinal pattern, combined pattern and complex pattern, were calculated and compared. It is concluded that the complex pattern is superior to the longitudinal pattern and the combined pattern in enhancing braking performance on wet asphalt pavement.

4) The tire inflation pressure formulates a positive influence on improving skid resistance of the wet asphalt pavement. When tire inflation pressure increases from 120 to 360 kPa, the vehicle braking distance decreases from 62.1 to 46.0 m.

5) The wet friction coefficient increases with the increase in the MPD. This tendency becomes more obvious when the vehicle speed increases. When MPD increases from 0.33 to 0.85 mm, the wet friction coefficient increases by 18.9%, 46.9%, 133.3% and 511.1%, respectively, corresponding to the vehicle speeds of 20, 40, 60 and 80 km/h.