变压器无功补偿的经济运行测算与分析
2019-01-17朱毅
朱 毅
(福建水利电力职业技术学院 机电工程系,福建 永安 366000)
0 引 言
为减少变压器及供电线路损耗,提高供电电压质量,通常是在供电变压器的负载侧适度并联无功补偿电容器以提高功率因数,目前一般是将供电功率因数控制在cosφ=0.9~1.0之间。但由于变电所变压器的供电负载时常是变动的,针对负载无功负荷的变化,在负载侧对应投入的电容器容量大小也应随之改变。这种做法只考虑并联电容器提高功率因数可以减少变压器供电损耗一个方面,未考虑到由于并联电容器容量的增加,会增大电容器介质损耗的因素,这是研究变压器供电经济运行时应综合考虑到的因素。因此,分析变压器无功补偿的经济运行应该是基于变压器供电损耗和并联电容器介质损耗之和的总损耗最小的基础上,分析影响变压器无功补偿经济运行的因素,研究变压器并联单组电容器补偿时电容器投入和切除的临界负载及经济运行的节电效果,以及并联不同组数电容器时的经济运行负载区间和节电效果。
1 单组电容器无功功率补偿的经济运行
图1所示,变电所内有多台并列运行双绕组变压器,负载侧安装一组电容器作为无功功率补偿用。在分析并联无功功率补偿电容器时,电容器产生的介质损耗和切除电容器时要增加变压器损耗的情况下,我们从变压器供电损耗和并联电容器介质损耗之和的总损耗最小的前提下,来分析投运电容器和切除电容器的临界条件及其节电效果。

图1 单组电容器无功功率补偿接图
1.1 投入电容器前的变压器有功功率损耗
电容器未投入无功功率补偿运行时的变压器有功功率损耗ΔP1计算式为:
(1)
式中:p0m—m台变压器的空载损耗之和,kW;
P2—变压器负载侧的有功功率,kW;
Q2—变压器负载侧的无功功率,kVar;
pkN—变压器额定负载损耗,kW。
1.2 并联电容器后的变压器有功功率损耗
无功补偿电容器投入运行后的变压器有功功率损耗ΔPC计算式为:
(2)
式中:QCI—电容器组的额定容量,kVar;
tanα—电容器的介质损耗因数,kW/kVar。
1.3 投入与切除电容器经济运行的临界负载
当ΔP1<ΔPC时投入电容器为经济运行,反之当ΔP1>ΔPC,切除电容器为经济运行。因此,令ΔPC=ΔP1,求解可得出投入与切除电容器的无功功率临界负载的Q2L(kVar)的计算式为:
(3)
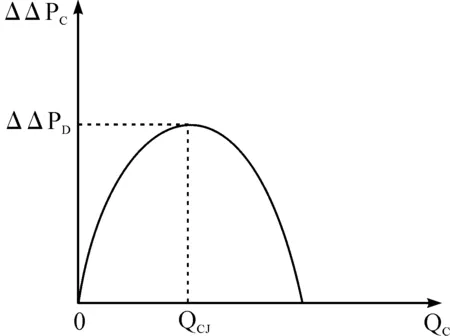
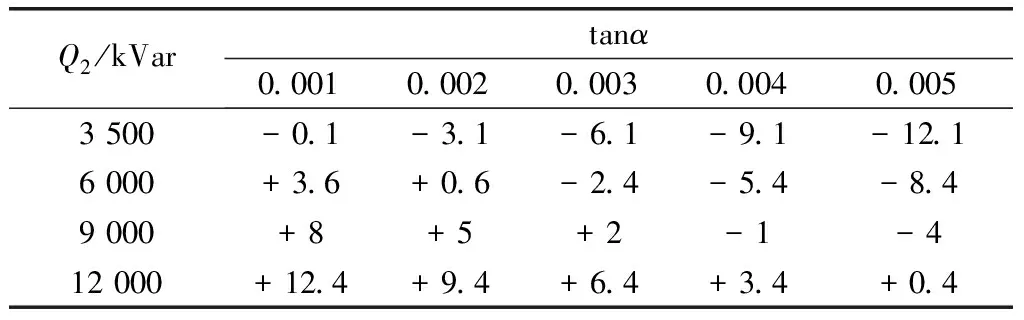
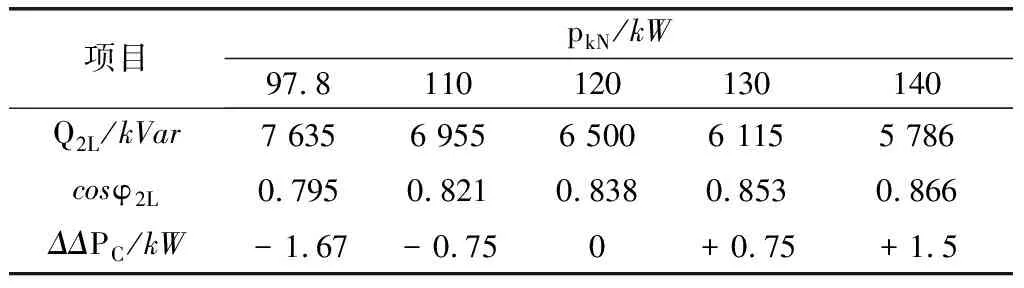
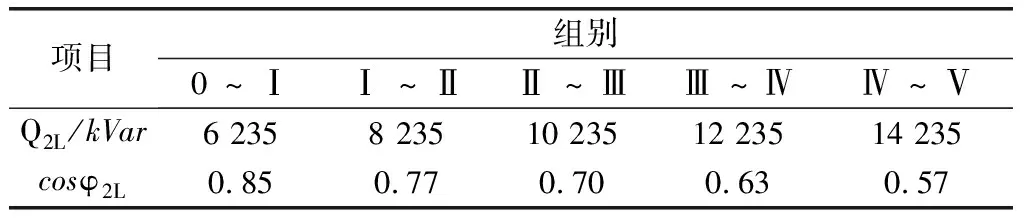
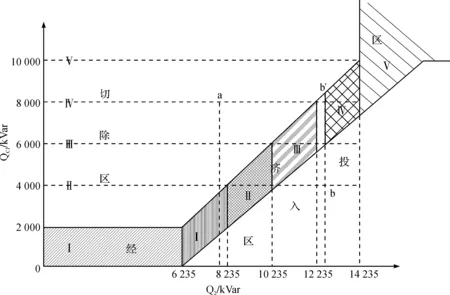
当工况负载Q2>Q2L时投入电容器为经济运行,反之当Q2 把临界负载Q2L代入功率因数计算式,则可得投入与切除电容器的临界功率因cosφ2L的计算式为: (4) 当工况负载cosφ2 把式(1)中的ΔP1减去式(3)中的ΔPC,可得投入电容器节约的有功功率ΔΔPC(kW),反之ΔPC-ΔP1可得出切除电容器节约的有功功率ΔΔP1(kW)计算式为: (5) (6) 无功功率补偿电容器的经济容量是指在工况负载条件下,投入电容器的容量取得最大节约功率。把式(5)中的电容器组容量改为电容器可变容量QC,则可改写成为下式: (7) (8) 按电容量经济容量QCJ进行无功功率补偿时,其节电效果最佳,其节约的功率ΔΔPC计算式为: (9) 图2 电容器投入功率节约曲线图 图3为在有多台并列运行双绕组变压器情况下,由于负载的无功功率波动很大,通常要在负载侧安装多组无功补偿电容器。在增加投运电容器组数时,虽然减少了损耗,但却增加了电容器的介质损耗;反之如减少电容器投运组数时,虽然减少了变压器损耗,但却增加了电容器的介质损耗;反之如减少电容器投运组数时,虽然减少了电容器的介质损耗,但却增加了变压器损耗。我们同样从变压器与电容器总损耗最小的前提下,分析和计算增加电容器组数和减少电容器组数的临界条件及其节电效果。 图3 多组电容器无功功率补偿接线图 原来是N组电容器运行和减少1组即(N-1)组电容器运行时的功率损耗ΔPN(kW)和ΔPN-1(kW)计算式: ΔPN=p0m+ (10) ΔPN-1=p0m+ (11) (12) (13) 设多组电容器组数为D,设少组电容器组数为X,那么可分别给出增加电容器组数经济运行节约的功率ΔΔPD(kW)和减少电容器组数经济运行节约的功率ΔΔPX(kW)的计算式为: (14) (15) 限于本文篇幅有限,我们仅就我市西门变电站中的一台变压器采取电容器无功补偿经济运行进行分析研究。 变压器SN=20 000 kVA,其技术参数为p0=18 kW,pkN=97.8 kW,负载侧有一组电容器进行无功功率补偿,计算以下几种工况负载条件下电容器的经济运行及其节电效果。 现分几种工况负载情况分析如下。 (1)当P2=10 000 kW,Q2=10 000 kVA、QCI=10 000 kVar、tanα=0.005,工况负载条件下,若cosφ1=0.876,可计算投入电容器在cosφC=1时的节电效果。 首先计算出: (Ω) 然后把已知的相关数据代入式(5)中,可计算出投入电容器节约的电功率ΔΔPC(kW)为: ΔΔPC=(2×10 000×10 000-10 0002)×24.45×10-8-10 000×0.005=-25.5 kW 由上述计算结果可知,把功率因数从0.876提高到1(完全补偿),不仅不节约电,反而多耗电功率25.5 kW,每年则多浪费电能近22万多kW·h。 采用本文前面式(3)和式(4)分别计算出投入和切除电容器的临界负载Q2L(kVar)及临界功率因数cosφ2L。 由以上计算结果可知,当工况负载Q2>15 225 kVar,或工况负载功率因数cosφ2<0.481时才能投入电容器,本实例上述情况中,因实际工况负载Q2=10 000<15 225 kVar及实际功率因数 cosφ2=0.876>0.481,故应切除电容器运行更经济。 (2)当P2=12 000 kW,Q2=15 000 kVA、cosφ1=0.56、QCI=15 000 kVar,且tanα=0.005、0.004、0.003、0.002、0.001的5种条件下时,分析计算临界负载、临界功率因数及投入电容器补偿到cosφC=1时的节电效果。分析如下: 分别根据本文上面的公式(3)—式(5)计算出Q2L、cosφ2L及ΔΔPC,其计算结果(见表1)。 表1 电容器经济运行的临界负载及节电效果 由表1可知,由于电容器介质损耗因数tanα的不同,临界负载Q2L变化范围为9 545~17 725 kVar,临界功率因cosφ2L数变化范围为0.49~0.72。投入电容器把cosφ提高到1时,其节电效果变化较大。如工况负载Q2(15 000 kVar)>Q2L(13 635、11 590、9 545 kVar)及工况功率因数cosφ2(0.56) (3)当QCI=3 000 kVar,而工况负载分别为Q2=3 500、6 000、9 000、12 000 kVar与电容器介质损耗因数tanα=0.001、0.002、0.003、0.004、0.005时,分析计算投入电容器的节电效果。 我们根据文中上述式(5)可分别计算投入3 000 kVar电容器后,5种不同工况负载Q2与5种不同电容器介质损耗因数时的有功功率节约值ΔΔPC,计算结果(见表2)。 表2 投入电容器的功率节约ΔΔPC kW 由表2的计算结果得知,投入电容器的节电效果:一是与工况负载Q2值大小密切相关,随着增大其节电效果增大;二是与电容器介质损耗因数密切相关,随着tanα减少其节电效果增大。 (4)当P2=10 000 kW,Q2=65 000 kVA、cosφ1=0.56、QCI=3 000 kVar,tanα=0.003,而变压器的短路损耗分别为pkN=97.8 kW、110 kW、120 kW、130 kW、140 kW,计算不同pk条件下的电容器经济运行的临界负载Q2L、临界功率因数cosφ2L及投入电容器后的节电效果。 同样可以根据本文中的前述计算式可计算出不同pkN条件下的Q2L、cosφ2L及ΔΔPC值(见表3)。 表3 不同pkN条件下的Q2L、cosφ2L、ΔΔPC 由表3得知:①由于实际工况Q2(6 500 kVar) 同样选取前例中的变压器SN=20 000 kVA,p0=18 kW,pkN=97.8 kW,rkM=24.45×10-8(Ω),负载侧共有5组电容器,每组电容器容量相等,QCI=2 000 kVar,tanα=0.003,分别分析计算以下几种不同条件下电容器的经济运行及其节电效果。 (1)对5组电容器经济运行区间划分 首先根据文中前述公式(12)、(13)分别计算不同组数电容器经济运行的临界负载Q2L及临界负载功率因数cosφ2L,其计算结果(见表4),并可绘制出并列电容器不同组数的经济运行区间图(见图4)。 表4 不同组数经济运行的Q2L、cosφ2L 图4 多组电容器的经济运行区间图 图4的横坐标表示工况负载Q2,纵坐标为电容器容量,Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ表示电容器组数,横坐标已给出电容器组的经济运行区间和临界负载Q2L。如Ⅰ组电容器的经济运行区间Q2=6 235~8 235 kVar,Ⅳ组电容器经济运行区间为Q2=10 235~14 235 kVar;当工况负载Q2<12 235 kVar时,应为Ⅱ组电容器经济运行,反之Q2>10 235 kVar时,则为Ⅲ组电容器经济运行。 如:当工况Q2=8 000 kVar,Ⅳ电容器投入QCI=4×2 000=8 000 kVar。此种情况下cosφ2=1,但工况点a在图3中切除区,由于Q2=8 000 kVar时是在Ⅰ组电容器经济运行区间a点,因此该情况下应切除三组电容器,由Ⅳ组电容器变成Ⅰ组,可根据文中前述公式(15)计算出减少电容器组经济运行节约的功率ΔΔPX。 Ⅰ组电容器运行时,其功率因数仅为cosφ2=0.857,由此可见,功率因数从1降到0.857时,反而节约功率9.18 kW,全年则可节约电能约8万kWh。 又如:当工况Q2=13 000 kVar,Ⅱ电容器投入QCI=2×2 000=4 000 kVar。此种情况下工况点b在图4中的投入区,由于Q2=13 000 kVar时是在Ⅳ组电容器经济运行区间b点,因此次情况下应在投入两组电容器,由Ⅱ组变成Ⅳ组,可根据文中前述公式(14)计算出增加电容器组运行的经济运行节约的功率ΔΔPD。 ΔΔPD=[2(4-2)×13 000×2 000-(42-22)×2 0002]×24.45×10-8-(4-2)×2 000×0.003=(13.69-12)=1.69 kW由Ⅱ组电容器运行增加到Ⅳ组电容器运行,其节约功率1.69 kW,全年节电量近1.5 万kW·h。 通过文中结合实例分析,我们可以得出以下几个结论:(1)变压器供电在其负载侧并联电容器,在某些情况下不一定能节电,必须综合考虑到补偿电容器介质损耗增加的影响;(2)变压器并联电容器经济运行主要与工况负载Q2、电容器介质损耗因数tanα和变压器短路损耗pkN三个因素密切相关;(3)变压器供电负载并联电容器无功补偿的经济运行与工况负载大小不直接相关。因此,我们在实际变压器供电运行管理中要改变完全依靠投入电容器提高功率因数的节电降耗的通用做法,应该全面实施变压器和电容器的经济运行管理才能达到供电网节电降耗的目的。1.4 投入与切除电容器经济运行的临界功率因数
1.5 投入与切除电容器经济运行节约的有功功率
1.6 无功功率补偿电容器的经济容量
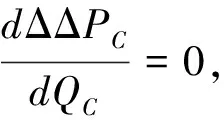
2 多组电容器无功功率补偿的经济运行

2.1 不同组数电容器投运的功率损耗
2.2 N组和(N-1)组电容器经济运行的临界负载
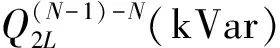
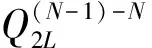
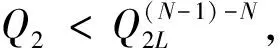
2.3 电容器经济运行的节约功率
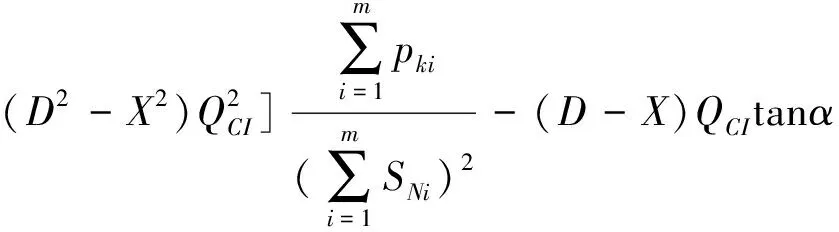
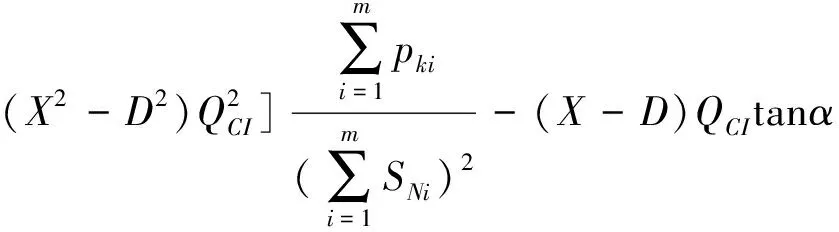
3 实例分析
3.1 实例一

3.2 实例二
4 结 语
