并联供水水库联合调度规则最优性条件研究Ⅰ:理论分析
2019-01-15胡铁松
曾 祥,胡铁松,王 敬,王 欣,汪 琴
(武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
1 研究背景
水库调度规则最优性条件是科学制定水库调度运行策略的理论基础,也是实际应用中确定水库蓄放水次序的重要依据,不合理的水库调度运行策略会增加水库群系统风险、提高水库弃水概率、降低系统综合效益,研究水库调度规则最优性条件具有重要理论价值与实际指导意义。
目前国内外关于水库调度规则最优性条件的研究较多,主要集中在单库供水量确定规则与并联水库蓄水量空间分配规则两个方面,提出了适用于来水不确定性较大的限制供水规则(Hedging rule)[1]以及来水分布较为一致的空间规则(Space rule)[2]与库容规则(Storage rule)[3]。由供水量确定规则与蓄水量空间分布规则组合构成的并联水库联合调度规则,在实际的水库群调度运行中得到了广泛使用,如标准供水策略(Standard Operation Policy,SOP)与空间规则的联合应用[4],限制供水规则(Hedging rule)与参数式规则(Parametric rule)的联合应用[5]。这种联合应用的调度规则虽然在一定程度上发挥了并联水库群的补偿调节作用[6],但存在联合应用的最优性条件不清晰的问题。一方面,总供水量确定规则与蓄水量空间分布规则的最优性条件,分别是在单库供水效益最大化与并联系统时段末蓄水效益分配最优化的两种模型理论框架下推求得到的,缺乏统一理论框架下联合应用调度规则的最优性条件挖掘与分析[6];另一方面,现有的调度规则未能表示出类似于限制供水规则启动标准与停止条件的水库可利用水量阈值范围,难以给出明确的水库最优调度运行指令。因此,有必要进一步开展并联供水水库联合调度问题最优性条件的研究工作,从理论层面推求联合调度规则的最优性条件,给出水库可利用水量阈值范围,从应用层面明确水库蓄放水优先次序及其划分标准,保障系统调度运行的最优性。
近年来,两阶段模型的建立为供水水库调度规则最优性条件的研究开辟了新途径。这类模型以边际效益相等原理作为理论基础,研究了供水量确定规则的最优性条件及其影响机理。Draper等[7]和Shiau[8]建立了单库两阶段供水调度模型,分析了不同调度目标下限制供水规则启动标准与停止条件的表述形式;You等[9]和Zhao等[10]分别讨论了来水不确定性以及约束条件对限制供水规则最优性条件的影响;Zeng等[11]拓展了两阶段调度模型的应用范围,给出了特定目标函数下并联水库总供水量确定规则的最优性条件。遗憾的是,上述理论研究成果仅适用于指导单库以及特定目标函数下并联水库的调度运行,关于并联水库联合调度规则最优性条件的一般性量化研究仍属于空白。
本文在胡铁松等[6]与Zeng等[11]研究工作的基础上,选取更具一般性的凸函数作为两阶段调度模型的蓄放水效益损失评价指标,采用库恩-塔克条件(K-T条件)求解模型,推导由总供水量确定规则与蓄水量空间分布规则组合构成的并联水库联合调度规则的一般性最优性条件,给出符合该最优性条件的水库可利用水量阈值范围以及蓄放水次序划分标准。理论分析结果表明:联合调度规则的最优性条件不仅对系统总可利用水量具有一定限制要求,而且要求成员水库可利用水量位于以系统总可利用水量作为自变量构成的阈值范围内。
2 并联供水水库联合调度规则最优性条件性质分析
2.1 并联供水水库两阶段调度问题最优性条件水库群联合优化调度的目标是为了寻求调度期内系统综合效益的最大化,或者损失的最小化。根据动态最优化理论,多阶段的水库优化调度问题可以描述为一系列由递归方程相衔接的两阶段优化决策问题。其中,并联水库系统两阶段调度模型的数学表达式如下[6]:
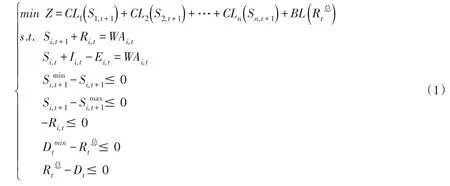
式中:Si,t为第t时段初第i个水库的蓄水量;Si,t+1为第t时段末第i个水库的蓄水量;Ri,t为第t时段第i个水库对共同用水户的供水量;Ii,t为第t时段第i个水库的来水量;Ei,t为第t时段第i个水库的蒸发渗漏水量;WAi,t为第t时段第i个水库的可利用水量,其定义为时段初水库蓄水量Si,t加上来水量Ii,t减去蒸发渗漏水量Ei,t;n为并联系统中成员水库的数目;为第t时段并联水库系统对用水户的总供水量,其定义为成员水库供水量之和,即为第t时段末第i个水库的蓄水效益损失函数;为第t时段用水户的供水效益损失函数分别为第t时段末第i个水库的下限与上限库容;为第t时段共同用水户的最低供水要求;Dt为第t时段共同用水户的供水要求。
由式(1)可知,上述两阶段模型主要适用于水库蓄水目标相互独立的情景,例如并联水库群的实时调度运行。针对供水调度问题,由于水库蓄水与供水效益损失函数通常具有凸函数性质[7],并且约束条件均为线性函数,因此,并联供水水库两阶段调度问题属于非线性凸规划问题。由库恩-塔克条件(K-T条件)可知,K-T条件是判定凸规划问题最优解的充要条件[10]。该模型的K-T条件为
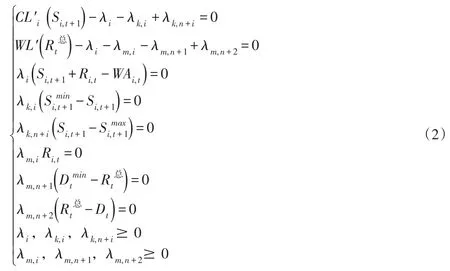
式中,λi、λk,i、λk,n+i、λm,i、λm,n+1、λm,n+2为拉格朗日乘子,经济学含义为相应约束条件的影子价格。当且仅当上述K-T条件(式(2))得到满足时,并联水库系统蓄放水策略集为模型最优解集。
2.2 并联供水水库联合调度规则仅考虑水库水量平衡方程对并联水库系统最优供水策略集的约束限制作用,即λi>0且λk,i=λk,n+i=λm,i=λm,n+1=λm,n+2=0时,由式(2)可知,成员水库供水边际成本与蓄水边际成本之间存在如下等式关系:
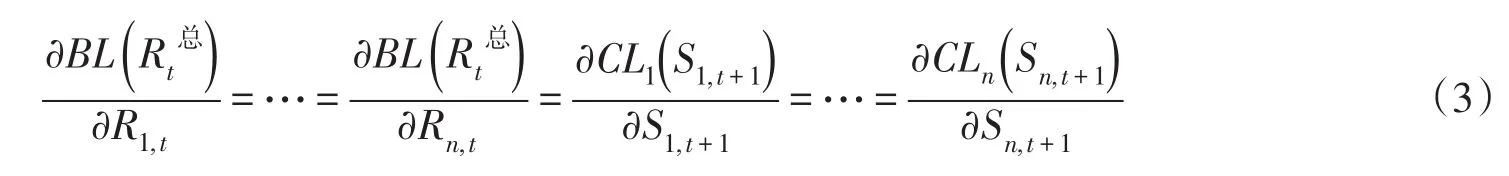
式(3)与经济学中边际效益相等原理的数学表述形式相一致,表明不同成员水库之间蓄水边际成本与供水边际成本均相等时,并联供水水库系统的综合效益损失最小[6]。
联立式(3)与水库水量平衡方程,可以推得并联水库系统时段最优总蓄放水决策分别为:
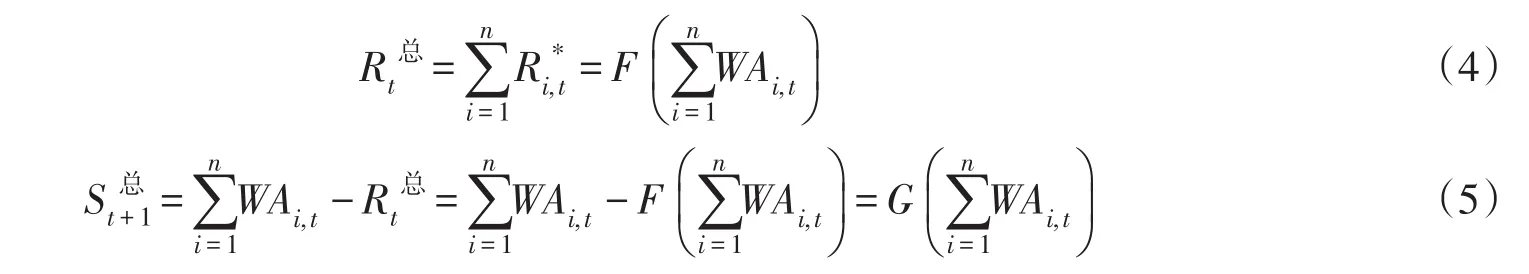
由式(4)可以看出,确定并联水库系统时段最优总供水量的数学表述形式符合总供水量确定规则的定义[11],表明采用以水库群总可利用水量作为自变量的供水规则,可以得到水库群系统时段最优总供水量。
与此同时,成员水库时段最优蓄放水决策的表达式分别为:
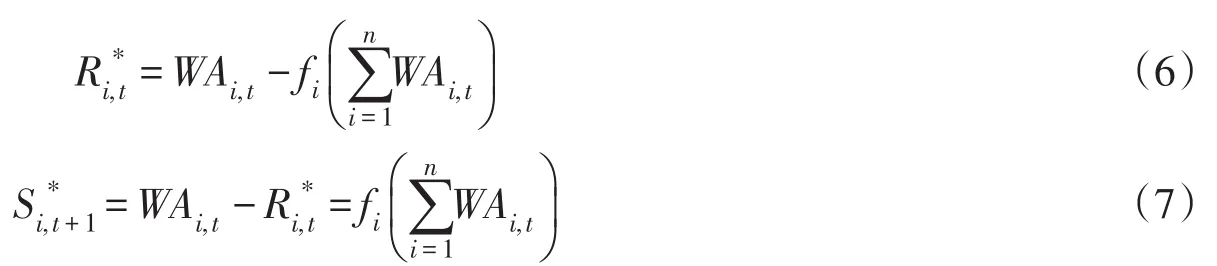
对比成员水库时段末蓄水量与并联系统总蓄水量的表达式可以发现,成员水库蓄水量可以通过系统总蓄水量进行表达:

确定水库时段末蓄水量的数学表达式(式(8))符合蓄水量空间分配规则的定义[11],表明采用以水库群总蓄水量作为自变量的蓄水量空间分配规则能够达到蓄水总量在各个水库之间最优分配的效果。
在此基础上,加入系统总供水量约束条件式(1)的限制作用,即λm,n+1+λm,n+2>0,由K-T条件可知,并联水库系统时段最优总供水量为起作用约束的边界值,与此同时成员水库最优蓄水量的分配遵循蓄水边际成本相等原理。类比水量平衡方程作用下成员水库蓄水量的推导过程,可以得到采用蓄水量空间分配规则仍然能够达到系统总蓄水量时段最优分配效果的结论。在此不作详细论述。
以上分析表明,在仅考虑水库水量平衡方程和并联水库系统总供水量约束条件的情况下,以边际效益相等原理作为理论基础,采用由总供水量确定规则与蓄水量空间分配规则组合构成的并联水库联合调度规则,在理论上可以同时实现系统供水与分配水最优化的目标。
2.3 并联供水水库联合调度规则最优性条件进一步考虑成员水库库容与供水量限制条件式(1)为优化调度模型有效约束的情景,即λi>0,λk,i+λk,n+i+λm,i>0且λm,n+1=λm,n+2=0,由K-T条件可知,水库供水边际成本与蓄水边际成本不再相等,成员水库最优蓄放水决策除了受蓄放水边际成本影响之外,还取决于水库时段最大最小容许蓄水量和供水量非负约束的限制。此时,成员水库存在以下4种供水决策情景:(1)λm,i>0,水库供水边际成本高于蓄水边际成本,水库以蓄水为主,不发生供水行为,最优供水决策由水库非负供水量约束条件决定,水库蓄放水边际成本相等,水库最优供水决策在水库蓄放水边际成本等价处取得;(3)λk,i>0,水库供水边际成本低于蓄水边际成本,水库以供水为主,供水行为直至库空状态结束,最优供水决策由水库下限库容约束条件决定水库供水边际成本高于蓄水边际成本,水库以蓄水为主,蓄水行为直至达到库满状态结束,最优供水决策由水库上限库容约束条件决定,
基于此,假设在并联水库系统中成员水库最优供水决策由水库非负供水量与上下限库容约束条件(即λm,i>0与λk,i>0、λk,n+i>0)决定的水库数目分别为p、q与o,其中p、q与o的交集为空集,则满足蓄放水边际成本相等原理的水库数目为h=n-o-p-q。此时,并联水库系统水量平衡方程为:
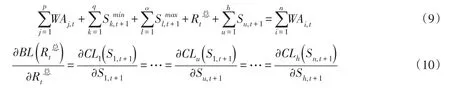
式(9)为并联水库系统水量平衡方程;式(10)为在此种情境下并联水库系统应满足的蓄放水边际成本等量方程。
由此,可以推得系统总供水量的表达式为:
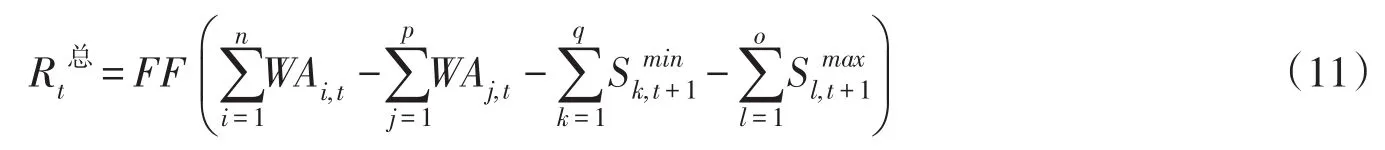
式(11)表明,并联水库群时段最优总供水量的确定需要同时考虑系统总可利用水量与不发生供水行为水库的可利用水量(如图1所示)。式(4)与式(11)的对比分析表明,仅参照系统总可利用水量的总供水量确定规则会将不满足水库非负供水量约束条件的供水决策考虑到总供水量的计算中,从而得到的系统总供水量小于最优值。因此,由式(4)表示的总供水量确定规则不能达到最优供水效果。值得注意的是,最优总供水量FF(·)和系统中有效约束条件数目p与q正相关、与o负相关。因此,并联系统总供水量的确定不仅受到水库自身供水量约束条件的影响,而且受到库容约束条件的限制作用。
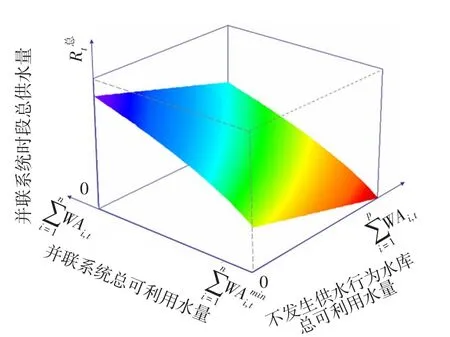
图1 考虑水库自身约束条件下并联水库系统时段总供水量
与此同时,水库时段最优蓄水量与库群时段最优总蓄水量分别为:
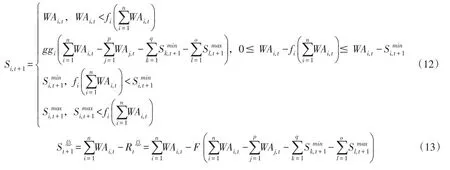
对比式(12)与式(13)可以发现,成员水库蓄水量与系统总蓄水量的确定不仅与系统总可利用水量相关,而且与不发生供水行为的水库总可利用水量相关,并且由式(12)表示的成员水库时段最优蓄水量难以直接通过库群时段最优总蓄水量(式(13))进行表述,因此采用蓄水量空间分布规则不能达到蓄水总量在成员水库之间最优分配的效果。
在此基础上,加入系统总供水量的约束作用,由K-T条件可知,取相应总供水量约束条件的边界值可以得到系统时段最优总供水量。类比前述水库蓄水量与系统总蓄水量的推导过程,可以得到如下结论:水库最优蓄水量由系统总可利用水量与不发生供水行为的水库可利用水量共同决定,而水库群总蓄水量的确定仅与系统总可利用水量相关。因此,通过蓄水量空间分布规则的应用,难以直接确定成员水库时段末最优蓄水量。
综上所述,当成员水库自身库容或供水量限制条件为两阶段调度模型有效约束时,采用由总供水量确定规则与蓄水量空间分布规则组合构成的并联水库联合调度规则难以保障水库群联合调度运行的最优性。即并联供水水库联合调度规则的最优性条件为成员水库同时向用水户进行供水,且不发生水库库满或库空的情景。值得注意的是,该最优性条件是在并联供水水库两阶段模型的理论框架下推求得到的结论,因此该最优性条件主要适用于此类并联水库两阶段调度问题。
3 并联供水水库联合调度规则最优性条件量化分析
3.1 可利用水量变化的阈值范围由成员水库时段最优蓄放水决策的表达式(式(6))可知,满足水库上下限库容约束条件的系统总可利用水量变化范围为:
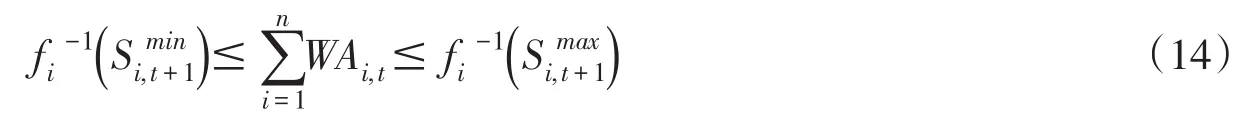
式(14)表明,当并联系统总可利用水量不低于成员水库下限库容阈值且不高于上限库容阈值时,成员水库库容限制条件不起约束作用。特别地,在每个水库库容上下限相等时所有水库将同时达到库满与库空状态。
同理,满足成员水库自身供水量约束条件的可利用水量变化范围为
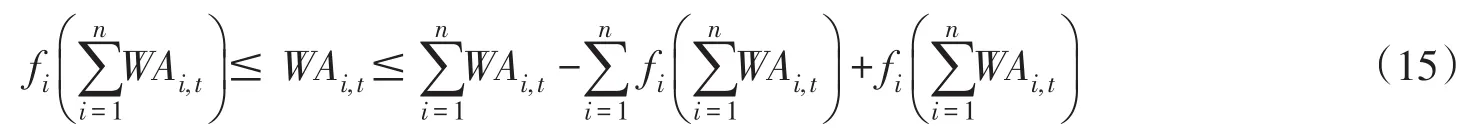
由式(15)可知,当成员水库可利用水量均位于式(15)所示区间内(图2中Ⅱ区)时,所有水库同时向用水户进行供水,成员水库供水量约束条件始终能够得到满足;当成员水库可利用水量过低,即(图2中Ⅲ区)时,成员水库处于蓄水状态,不发生供水行为;当成员水库可利用水量过高,即(图2中Ⅰ区)时,成员水库处于供水状态,并且会导致并联系统中其余水库不发生供水行为(图2中Ⅲ区)。
因此,成员水库的蓄放水决策行为会受到其他水库可利用水状态的影响,一方面随着其余水库可利用水量的降低,该水库发生供水行为的概率与发生库空状态的概率均会升高,另一方面随着其余水库可利用水量的增加,该水库发生库满状态的概率则会升高。特别地,如若其余水库总可利用水量趋近于阈值时,水库的供水行为与供水至库空行为将会同时出现;但若总可利用水量高于此阈值,水库会优先发生不供水行为;反之,总可利用水量低于此阈值,水库会优先供水至库空状态。
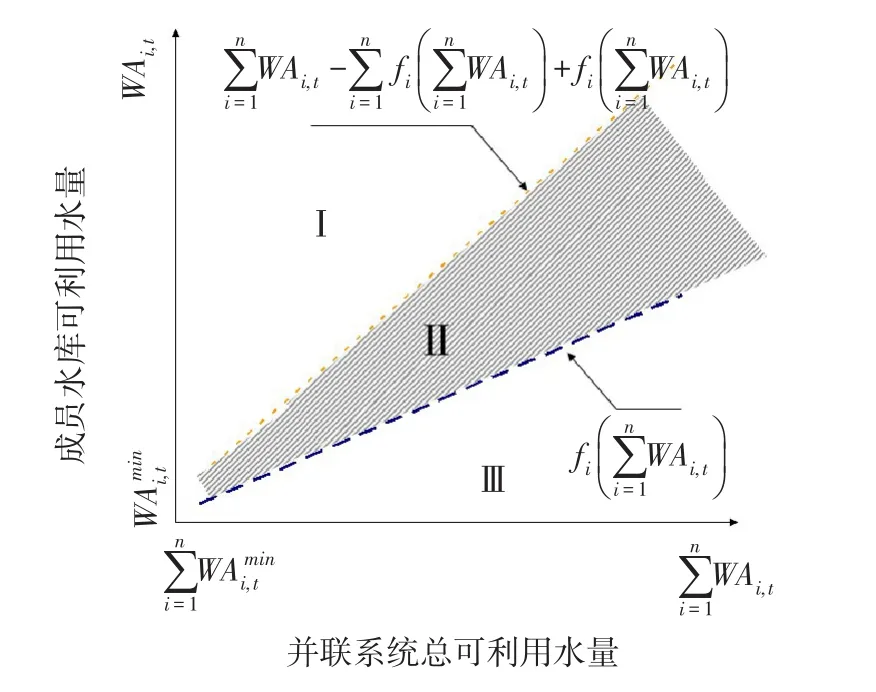
图2 符合水库自身供水量约束条件的水库可利用水量阈值范围
综上,当且仅当并联系统总可利用水量与成员水库可利用水量同时位于式(14)与式(15)所示区间内时,由总供水量确定规则与蓄水量空间分配规则构成的联合调度规则才是最优的调度规则。
3.2 水库蓄放水优先次序若水库蓄放水效益损失函数边际成本的初始值相等(CL′i(0)=CL′j(0)=BL′(0)),且其二阶导数比恒为常量时,如凸函数为二次项表达式,成员水库可利用水量阈值范围可简化为:

其中:

式中:Ai,t为常量,其取值由成员水库自身蓄水效益损失函数与其余效益损失函数的二阶导数比确定,并且的取值位于0到1之间;θi,t为成员水库可利用水量与并联系统总可利用水量的比率。
此时,水库可利用水量比率θi,t可以作为水库蓄放水优先次序的判定标准,其中,Ai,t是判定成员水库i能否作为被补偿水库的可利用水量比率阈值,若水库可利用水量比率θi,t低于Ai,t,成员水库应当作为被补偿水库,优先执行蓄水操作;同样是判定成员水库i能否作为补偿水库的可利用水量比率阈值,若水库可利用水量比率成员水库应当作为补偿水库,优先执行供水操作。
为了进一步探讨水库库容大小,调节性能高低以及蒸发能力强弱对水库供水优先次序的影响作用,本文定义水库实时调节性能与库容蒸发比分别为:

式中:μi,t为第t时段成员水库i库容与来水量的比值,用来衡量水库调节性能的高低,μi,t越大表示水库i在第t时段的调节能力越优,反之亦然;ηi,t为第t时段下水库蒸发量与库容的比值,用来衡量水库蒸散发能力的强弱,ηi,t越大表示单位库容下水库蒸发量越多,反之亦然。
基于此,成员水库可利用水量比率可表示为如下形式:
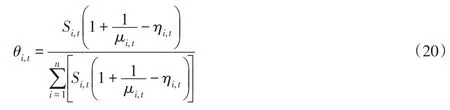
由式(20)可知,当水库库容较大,但调节性能较差,蒸散发能比较弱时,成员水库越适合作为补偿水库优先供水;相反,当水库库容较小,但调节性能较优,蒸散发能力较强时,成员水库越适合作为被补偿水库优先蓄水。特别地,若某成员水库库容远大于其他水库库容,即θi,t趋近于1时,其他水库的可利用水状态对本水库调度决策行为的影响作用较小,该水库承担主要供水任务,始终处于供水状态;反之,若某成员水库库容远小于其他水库库容,即θi,t趋近于0时,其他水库的可利用水状态对本水库蓄放水决策行为的影响作用较为显著,该水库不易于发生供水行为,始终处于蓄水状态。因此,根据以上3个指标在一定程度上可以判定水库蓄放水的优先次序。
4 结论
本文以并联水库系统两阶段联合调度模型作为理论基础,采用K-T条件作为求解技术,推导了并联水库联合调度规则的一般性最优条件,给出了满足最优性条件下水库可利用水量变化的阈值范围以及补偿水库与被补偿水库的划分标准。理论分析结果表明:(1)所有成员水库同时向用水户进行供水,且没有出现库满或库空的调度情景是由总供水量确定规则与蓄水量空间分配规则组合构成的一类并联水库群联合调度规则的最优性条件,为满足该条件,并联系统总可利用水量和成员水库的可利用水量都应该在给定的阈值范围内变化。(2)特别地,若并联水库系统蓄放水效益损失指标为二次项的凸函数时,成员水库可利用水量与并联系统总可利用水量的比率可以作为水库蓄放水优先次序的判定标准。当水库可利用水量比率低于被补偿水库可利用水量比率阈值时,成员水库应当作为被补偿水库,优先执行蓄水操作;当水库可利用水量比率高于补偿水库可利用水量比率阈值时,成员水库应当作为补偿水库,优先执行供水操作。(3)补偿水库与被补偿水库的划分标准主要由水库库容,水库调节性能与库容蒸发比3个指标决定。当水库库容较大,但调节性能较差,蒸散发能比较弱时,成员水库越适合作为补偿水库优先供水;相反,当水库库容较小,但调节性能较优,蒸散发能力较强时,成员水库越适合作为被补偿水库优先蓄水。因此,根据以上3个指标在一定程度上可以判定并联水库系统蓄放水的优先次序。
模型的算法设计与实例研究将在下篇中给出。
