区域电离层延迟模型的建立及精度对比分析
2019-01-15李华圣詹达诲
李华圣,詹达诲,舒 宝
(1.国家无线电监测中心检测中心,北京 100041;2.武汉大学,武汉 430079)
1 引言
电离层延迟是GPS观测的主要误差源之一,对GPS测量来说这种差异引起的测距误差在天顶方向达50m,在接近地平方向时(高度角为20°)可超过100m,在最恶劣的条件下可达150m,因此有必要通过建立合适的电离层模型,有效降低电离层对GPS测量精度的影响。
现有的电离层延迟方法主要有差分法、双频改正、半合改正、模型法等,其中差分法只适合小区域,随着用户与基准站的距离越来越远改正效果越差,双频改正主要针对双频接受机,半合改正引入模糊度参数增加了数据处理的难度。模型法中现行的GPS用户最常用的Klobuchar模型只能消除60%左右的电离层延迟误差,而用双频观测值建立的区域电离层模型可以有很好的改正效果。本文主要用三角级数模型和多项式模型建立区域电离层模型并与双频改正与Klobuchar模型进行对比分析,最后对所建模型的GPS硬件延迟和接受机硬件延迟的稳定性进行了评价。
2 VTEC模型建立的原理
利用双频观测值不但可确定不同频率的观测值所受到的电离层延迟进而消除其影响,而且可测定穿刺点(卫星信号传播路径与中心电离层的交点)上的VTEC值。为了提高实测TEC的精度,首先对双频伪距观测值进行周跳探测[2],[3]和载波相位平滑[7]。其与Klobuchar模型相似,实际上也是一个单层模型,关键在于求得穿刺点处的VTEC值,然后根据穿刺点处的VTEC值来拟和出该时段的电离层延迟改正模型。

将f1和f2的具体数值代入后可得伪距观测值

式中,TEC以1016个电子/m3,为单位;P1、P2以m为单位;BS、BR分别为卫星和接受机的硬件延迟,可通过参数估计计算。
然后用下式求得穿刺点上的VTEC值:

式中,Z为穿刺点上卫星的天顶距。
3 多项式模型和三角级数模型的建模方法
VTEC多项式模型POLY(Pl oy nom i n a l Model)是目前广泛应用的局部电离层模型,但一般只能在数小时的拟和过程中达到较好的精度,单层电离层多项式展开模型是将VTEC看作是纬度差和太阳时角差 的函数。其具体表达式为:
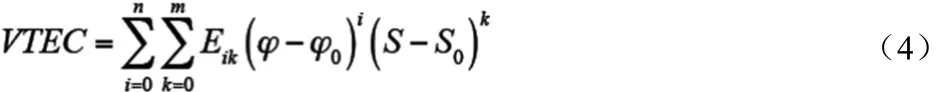
式中,ö0为测区中心点的地理纬度;S0为测区中心点(ö0,λ0)在该时段中央时刻 t0时的太阳时角 S-S0=(λ-λ0)-(t-t0);λ为信号路径与单层的交点P'的地理纬度;t为观测时刻。当观测时段长度为4h,测区范围不超过一个洲时,泰勒级数展开式中的最佳阶数为:ö-ö0项取1-2阶,时角S-S0项取2-4阶。
Geosriadous利用三角级数函数TSF(Trigono-metric Series Function)进一步提高了局部电离层模型延迟周日变化特性的模拟能力。特别是广义三角级数函数GTSF(Generalized Trigonometric Series Funcetion)将TSF扩展为地磁参考系下,参数可调,能够有效模拟长测段电离层延迟。在编制程序时,其公式可写成:
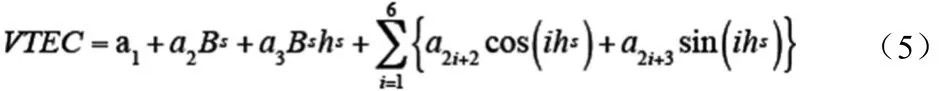
式中,BS是卫星穿刺点的足下点纬度与展开点纬度之差,其计算公式为:

式中,öi为穿刺点的地理纬度;λi为地理经度。

式中,T代表一天的24小时;t是观测时刻穿刺点的地方时。
4 实例分析
本文用20 0 9年年积日100天的数据用三角级数模型和多项式模型两种方法建立的单站模型与实测值的精度比较。表1是两种模型在不同纬度区域拟合的内符合精度,是以公式δ=评定的。其中n是穿刺点个数,v是每个穿刺点对应的VTEC拟合残差。它们的大地坐标纬度和经度分别是:bjfs(39.60,115.89),wuhn(30.53,114.35),twtf(24.95,121.16)。
由表1可以看出多项式拟合的精度要好于三角级数模型,随着纬度的降低两种模型的拟合精度都越来越差,主要原因是随着纬度的降低电离层越来越活跃。
为了进一步验证两种模型在不同区域的精度,本文采用中国区域及周边的11个IGS基(bjfs,khaj,chan,lhaz,xian,wuhn,twtf,shao,urum,guao,ulab)2009年年积日100天数据分别用三角级数和多项式模型拟合中国区域上空的总电子含量分布。根据两模型的特点多项式模型采用3*4阶,分12个时段拟合,三角级数模型全天15参数(不包括接收机和卫星硬件延迟参数),图2是11个IGS基站上空穿刺点分布图。
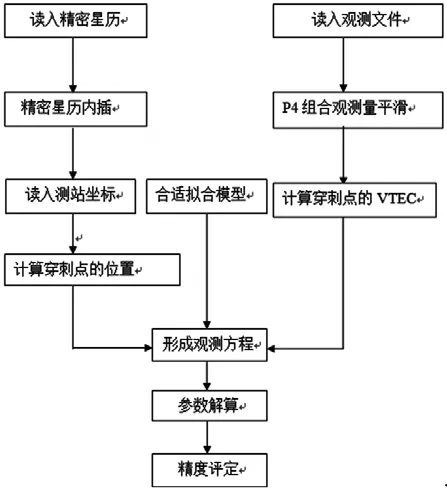
图1 单站模型三角级数、多项式模型计算的VTEC值与实测值的比较
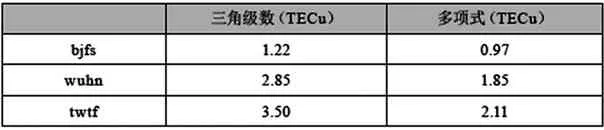
表1 单站模型在不同区域的拟合残差
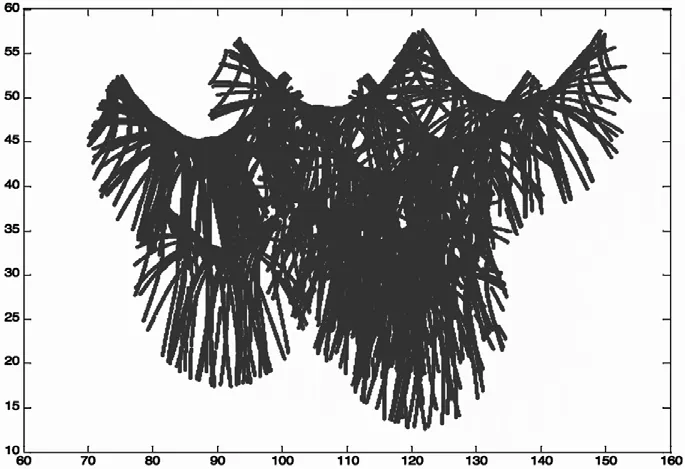
图2 中国区域上空穿刺点分布图
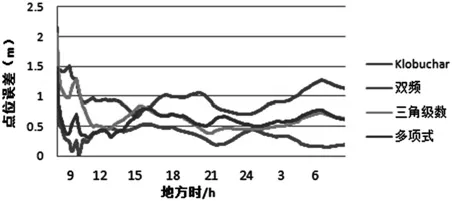
图3 bjfs站不同电离层延迟改正的比较
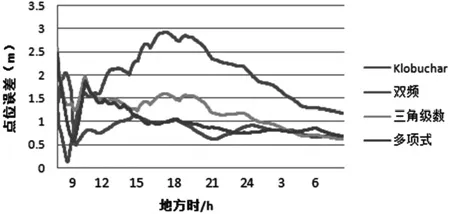
图4 shao站不同电离层延迟改正的比较
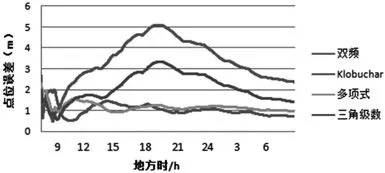
图5 twtf站不同电离层延迟改正的比较
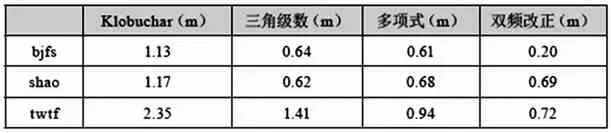
表2 中国不同纬度区域不同模型的定位精度比较
由图2可以看出,11个基站的数据基本能覆盖中国区域,分别用上述数据计算的三角级数和多项式模型系数为单频静态单点定位程序提供电离层改正。选取国内区域不同纬度区域的3个IGS基站的数据进行单点定位分析。比较三角级数、多项式模型、Klobuchar模型、双频在这不同纬度区域的三个站(bjfs,shao,twtf)的电离层改正精度。图3、图4、图5分别是这三个站的单点定位随时间变化静态解与真值点位误差结果,表2是单点定位的全天解点位误差结果。
由图3、图4、图5和表2可以看出:一是在纬度相对较高的区域三角级数模型、多项式模型的电离层改正效果都较好,Klobu-char的改正效果稍差。二是随着纬度的降低,三角级数和Klobuchar模型的效果越来越差,而多项式模型的效果相对较好。原因是多项式模型是分时段拟合,在电离层活跃时也可以有很好的拟合效果。三是所建的模型基本能覆盖全国区域,对区域内的单频用户的电离层改正可以有较好的效果。
电离层建模中DCB一般按单天解算,DCB的精度和稳定性可作为模型精度的反映。图6是2009年年积日88天数据卫星DCB的与CODE比较结果,多项式模型中的卫星硬件延迟参数采用和CODE球谐函数模型同样的约束:qi=0,qi是第i颗卫星的硬件延迟。由图6可以看出差值大多数在0.2个ns左右。图7是88-104天卫星硬件延迟比较,CODE的卫星延迟更为稳定,原因是CODE采用全球200多个IGS基站的数据,观测的卫星的数据量大。多项式模型计算的卫星的STD标准差在0.1ns左右,基本是可靠的。

图6 卫星硬件延迟比较
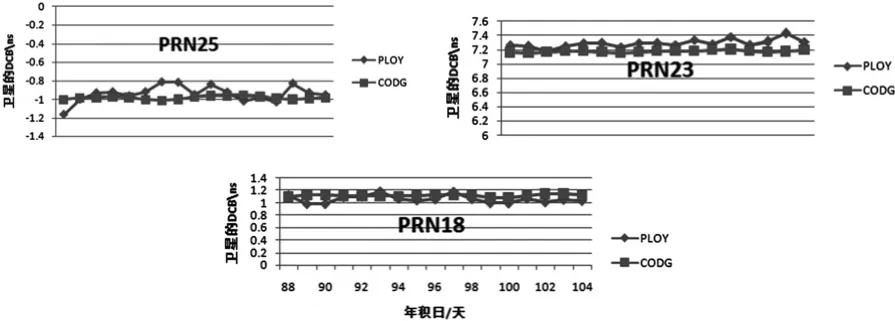
图7 卫星硬件延迟随时间的变化
接收机硬件延迟偏差稳定性也是衡量电离层模型化精度的重要手段。图8、图9是CODE和多项式模型计算的接收机硬件延迟比较。由图可以看出相对卫星的DCB,接收机DCB的稳定性要差,多项式模型计算的接收机DCB的稳定性与CODE基本相当。
5 结束语
用双频观测值建立的区域电离层模型的精度明显优于Klobuchar模型,能为区域内的单频GPS 用户提供较好的电离层改正。其中全天参数的三角级数模型在纬度相对较高的区域改正效果较好,在电离层活跃的低纬地区分时段的多项式模型也可以表现出较好的效果。DCB分析表明多项式模型所建立的中国区域的电离层改正模型是可靠的。
