多模GNSS星间偏差估计及其在定位中的应用
2019-01-15李华圣徐龙威
杜 昊,李华圣,徐龙威
(1.国家无线电监测中心检测中心,北京 100041;2.武汉大学,武汉 430079)
1 引言
随着GNSS产业的飞速发展[1],多模GNSS组合逐渐成为改善卫星导航定位性能的重要手段[2]。由于GNSS系统基于不同的时间系统、坐标系统、载波频率、信号调制方式以及轨道平面,主要采用引入系统间偏差(inter system bias,ISB)的方式实现多模GNSS系统间兼容和互操作[3-5]。多模GNSS组合单点定位中通常将采用一个系统对应一个接收机钟差参数的模式,参数之差即为ISB[6]。将ISB与接收机坐标一起作为未知参数解算是目前研究ISB变化规律的主要方法。文献[7]基于全球多个IGS跟踪站研究了不同类型接收机和不同频率GLONASS信号对应的GPS/GLONASS ISB,并将其研究成果用于GPS/GLONASS组合定位,明显改善了定位效果。文献[8]通过连续观测发现对于不同类型接收机GPS/GLONASS ISB不同但都十分稳定,日变化在cm级,可用多项式或随机过程模型模拟。文献[9]在分析CONGO网络测站性能时第一次提出GPS/Galileo测距码ISB并从理论上说明ISB与接收机和信号调制方式有关。MEGX 分析中心COM和GFM在BIAS SINEX Format文件中提供GPS-Galileo ISB,在45ns左右,存在0.7ns/d的日变化[10]。利用ISB与接收机有关且具有稳定性的特点,将ISB提前求出作为先验值播发给用户以减少观测模型未知参数,能够显著提高多模GNSS组合定位性能[11]。文献[12]和文献[13]将短时间内ISB作为常数,把观测值充足历元求得ISB用于观测值不足历元,在损失一定精度的条件下实现GPS/GLONASS双系统仅4颗星定位解算。
然而,可见卫星不足时,直接引入先验的ISB估值,虽可实现定位,但定位精度较差[14]。主要原因是,可见卫星太少,观测方程稳健性低和抗差能力差。本文提出一个新的参数估计方法,以GPS为基准,对其他GNSS系统每颗卫星分别计算一个偏差参数,该参数不仅包含ISB还包含了该卫星大部分的观测误差。然后,将该偏差参数用于可见卫星不足条件下的单点定位中。
2 数学模型
多模GNSS伪距观测方程如下:

式中,P 是伪距观测值;A,B 是两个 GNSS系统;i,j是卫星号;x,y,z是卫星坐标;x0,y0,z0为接收机坐标;dtAj是卫星钟差;dtr为接收机钟差;T是对流层延迟;I是电离层延迟;M是对流层延迟;ξ是观测噪声;c是光速。
GNSS基于不同的时间系统和坐标系统,首先应进行时空统一。基于RENIX 3.02数据格式利用式(3)~(5)将时间系统统一转换到GPST[15]。对于坐标系统,GPS-WGS84,GLONASS-PZ90.02,BDS-CGCS2000,Gal i leo-RTRF,WGS84、CGCS2000、GTRF 三者与ITRF2000差异很小本文忽略其差异,PZ90.02与ITRF存在分米级,PZ90.02与ITRF2000差异仅在XYZ方向分别平移-0.36m、+0.08m、+0.18m。
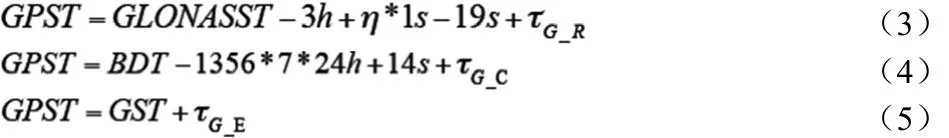
式中,τG_RτG_CτG_E分别为 GPST 与 GLONASST、BDST、GST 除去整秒偏差后的剩余时间差;n为UTC与TAI间的闰秒数;G 为GPS;R为GLONASS;C为BDS;E为Galileo。
利用最小二乘算法,ISB估值可用(6)表示:

式中,ξA为系统A中所有参与解算卫星未校正误差的加权平均值。将ISBA_B直接引入可见卫星不足历元,虽可以消除时间系统偏差,然而无法估计各颗卫星的未校正误差,因此本文提出一个新的参数。以系统A为基准,系统A所有卫星与系统B中卫星i一起解算,如式(7)~(8);同理系统A与系统B中卫星j一切解算。然后,用式(9)获得参数星间ISB参数ISBi_j,再用其对相应卫星的观测值进行修正,用于卫星数不足条件下定位。

式中,S为基准,GPS为首选;n为当前历元可见GPS卫星数;ρ为卫星与接收机的距离。在计算GNSS卫星轨道时需要采用相应的物理常数和轨道模型;进行卫星钟改正时顾及相对论相应,并采用广播星历播发TGD或BGD改正信号群延迟改正;对流层延迟改正采用Saastamoinen 模型;电离层延迟改正采用消电离层组合。
3 星间ISB特性分析
本文以MEGX提供的2015年3月31日CUT0站观测数据为例对星间ISB的特性进行分析,接收机类型为Trimble NetR9,采样间隔30s,截止高度角10°。
如图1所示,不同系统的卫星ISB差异明显,GLONASS与Galileo卫星 ISB 约10ns~30ns,BDS 卫星 ISB 一般在70ns~120ns。同一系统内,不同卫星ISB也存在差异,例如R20与R06许多历元相差15ns以上,BDS和Galileo也存在类似状况。对于BDS卫星,随着高度角的降低,ISB出现明显变大的趋势,其主要原因是:一是北斗卫星高度角偏差的影响,在卫星高度角10°左右时,北斗IGSO和MEO卫星存在1.5m左右的多路径效应。二是消电离层组合导致在进行数据处理时,观测噪声和多路径效应的影响被放大约3倍。图2为R14-G ISB在观测时段17:00-19:00变化规律,具有明显的周期性,且与GLONASS广播星历更新明显吻合,因此推断广播星历更新是G-R ISB的重要影响因素。需要指出的是,由于消电离层组合观测噪声被放大,广播星历对G-RISB的影响容易被淹没,但在估计ISB 是仍需顾及广播星历更新。

图1 不同卫星与GPS系统之间的偏差
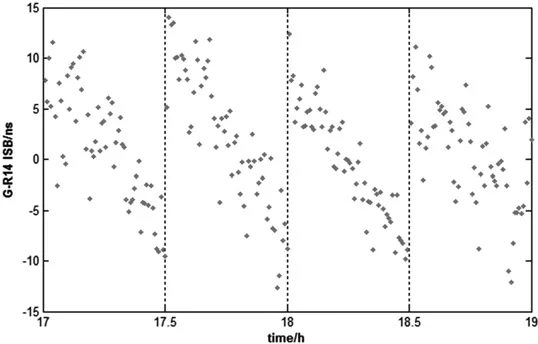
图2 R14-G ISB变化规律
以06:00-08:00观测时段为例分析星间ISB,如图3所示,选取观测时段内始终可见的四颗卫星R20、R06、C06以及E11。R20-R06星间ISB为同一系统内卫星间偏差,始终小于15ns,另外广播星历的影响也十分明显。R20-C06、R06-C14和C06-E11 为不同系统间的星间ISB,量级都在几十纳秒。
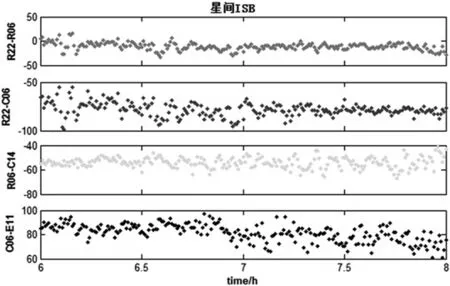
图3 以GPS为基准不同卫星星间ISB估值
4 实验分析
将卫星星间ISB用于可见卫星不足条件下的单点定位,并与引入传统的ISB参数进行对比分析。本文提出方法具体实施步骤为:一是存储一个可见卫星充足的历元并实时更新;二是在可见卫星不足历元,分析当前历元可见卫星号;三是估算相应的星间ISB;四是最后将星间ISB估值引入当前可见卫星不足历元,实现定位解算。
利用CUT0站2016年4月28日12:00-16:00观测数据,对本方法性能进行验证。PDOP阈值设置为40,历元间隔30s,截止高度角10°,每五分钟更新一次观测值充足存储历元。伪距单点定位一般用于低精度导航,为降低对用户的硬件要求,本实验利用klobuchar模型代替消电离层组合进行电离层改正,采用GPS广播星历发布的参数。
设计四种实验方案:一是1颗GPS,1颗GLONASS,1颗BDS,1颗 Galileo;二 是4颗GPS;三 是2颗GPS,2颗GLONASS;四是2颗GPS,2颗BDS。
参与解算卫星为随机选取,分别采用引入不顾及卫星号的ISB估值和顾及卫星号的星间ISB两种方式进行定位。首选GPS作为基准,在方案2和4中计算ISvB时以GLONASS作为基准。图4为各方案的定位结果,与传统ISB相比,星间ISB可以使定位精度和可靠性明显改善,其中方案1最明显。对于方案1,引入星间ISB后N、E、U三个方式的定位精度明显提高,可靠性和稳定性也明显改善。方案2采用4颗GPS卫星进行定位,采用新方法后对定位精度略有改进,但没有方案1明显,这主要是由于GPS 卫星间偏差较小,此时影响定位精度的主要因素是PDOP和观测值误差。另外,GLONASS广播星历更新对基准造成影响,方案2中E和U方向定位偏差曲线出现跳跃。由此可知,基准的精度会对星间ISB产生影响,寻求一个更加稳健的基准对兴建ISB解算具有重要意义。对于方案3和方案4,在N和E方向定位精度明显提高,但是定位可靠性略有降低。
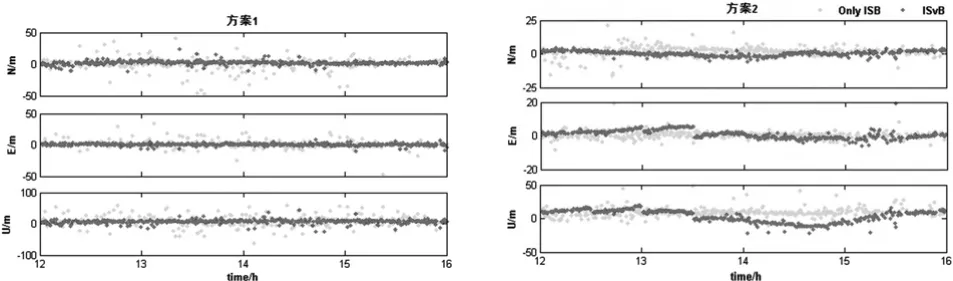
表1为定位结果统计,4种方案在引入星间ISB 后定位精度都有提高,水平方向定位偏差RMS都在10m以内,完全能够满足低精度用户的导航需求。方案4(2 GPS+2 BDS)定位精度优于方案3(2 GPS+2 GLONASS),可知GPS和BDS的兼容性优于GPS和GLONASS的兼容性。

图4 不同方案定位误差

表1 定位结果统计
5 结束语
在可见卫星不足条件下,仅引入先验的ISB减少多模GNSS伪距单点定位中钟差参数个数,虽可实现定位,但定位精度往往很差。本文提出一个星间ISB参数,在估计系统间偏差的同时,也考虑到具体卫星为校正误差想,并设计了多种方案进行多组实验,证明引入星间ISB后,定位结果得到了明显改善,4颗卫星可见条件下,水平方向定位误差在10m以内。
