同步坐标变换的径向混合磁轴承系统谐波干扰抑制方法*

2019-01-15郑世强

传感器与微系统 2019年2期

张凯，郑世强

(1.北京航空航天大学惯性技术重点实验室新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191；2.北京市高速磁悬浮电机技术及应用工程技术研究中心，北京 100191)

0 引言

与传统的机械轴承相比，磁悬浮轴承具有非接触、无摩擦、电磁力可控、精度高、噪声低、寿命长等优点[1]，广泛地应用在了磁悬浮鼓风机等高速旋转设备中，必将对我国工业化进程产生巨大的推进作用。

倍频谐波干扰对磁轴承控制系统的稳定运行和控制精度都具有很大的影响。目前，对倍频谐波干扰抑制的研究按照谐波干扰的次数可划分为单谐波干扰抑制和多谐波干扰抑制。对于单谐波干扰抑制，主要有自适应陷波器的方法[2]，但具有动态响应慢、计算量相对较大的缺点。而对于多谐波干扰抑制主要有重复控制器[3]、自适应多频率追踪法[4]等。重复控制器有构造简单的优点，但动态响应比较慢。自适应多频率追踪法的计算量会随着抑制的倍频数目的增加而显著增加。

而如果按照自由度划分的话，目前大部分研究方法主要针对径向平动两自由度的谐波进行抑制研究，如文献[5]利用重复控制器进行平动两自由度谐波电流的抑制。而同时对径向平动和转动4自由度的谐波干扰的研究相对较少，如文献[6]用自适应陷波器和重复控制器对在平动两自由度对谐波力进行抑制，在转动两自由度上对谐波力矩进行抑制。

本文中引入基于同步坐标变换的方法对平动和转动自由度的谐波同时进行抑制。用变量重构的方法对系统进行建模，分析了系统的收敛性和稳定性，并进行了仿真验证。在30 kW磁悬浮高速鼓风机仿真证明了该谐波抑制方法的有效性，与传统自适应陷波器相比具有更好的动态性能，计算量更小。

1 基于同步坐标变换的原理

基于同步坐标变换方法的基本思想为：将静止坐标系中的倍频分量通过同步坐标变换转换成同步坐标系下的直流分量。然后用低通滤波器识别该分量，同时过滤掉其他倍频分量，利用坐标逆变换将该倍频分量重新转换成静止坐标系下的倍频分量。然后用负反馈将该倍频分量抵消，原理如图1所示[7]。

图1 基于同步坐标变换方法的原理

1.1 传递函数推导

由于x通道和y通道的相位相差90°，故该系统可以用变量重构法来构建并求传递函数

xdc+jydc=(xo+jyo)e-j(kωt+θk)

(1)

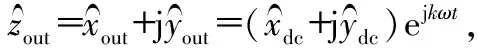
结合拉普拉斯变换的性质可得传递函数

(2)

可以得到陷波器的闭环传递函数

(3)

本文主要研究对3次谐波的抑制，即k=3。

1.2 收敛性证明

因为初始时刻输入的倍频信号经过坐标正变换后，倍频信号变为直流信号。所以可以将系统简化为图2所示的结构[7]。

图2 陷波器等效结构

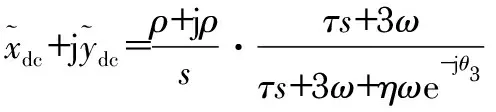
(4)

其中,输入的等效直流信号的传递函数为(ρ+jρ)/s，ρ为输入信号的幅值

(5)

第二项的幅值可以表示成

(6)

1+ηcosθ3>0

(7)

2 系统建模

2.1 径向四自由度的系统建模

根据文献[6，8],可以分别建立陷波器系统在平动两自由度和转动两自由度的子模型如图3、图4所示。

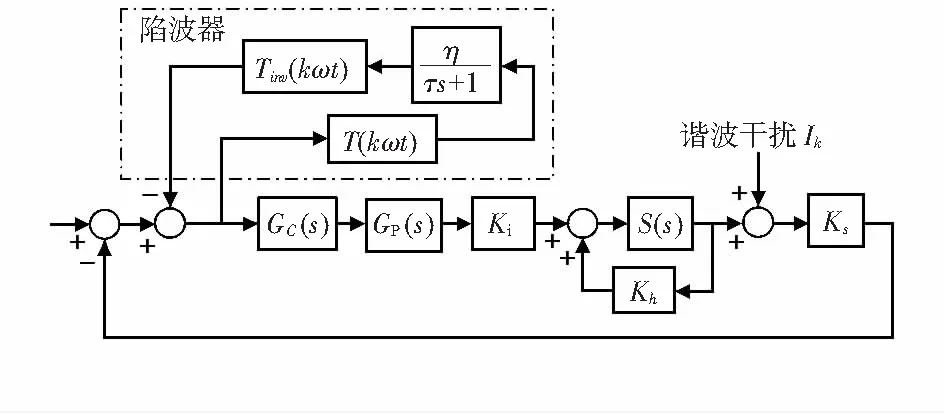
图3 平动子系统的抑制倍频扰动的结构

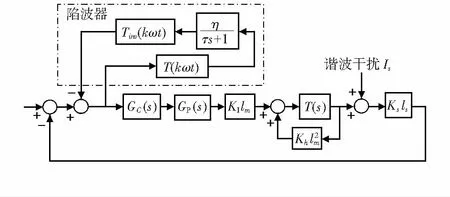
图4 转动子系统的抑制倍频扰动的结构

(8)

2.2 稳定性分析

平动子系统的开环传递函数为

(9)

转动子系统的开环传递函数为

(10)

平动子系统和转动子系统各有5个开环极点，其中有1个极点在原点上，有2个在左复半平面，1个在右负半平面,余下1个极点为

如果满足系统收敛的条件，即满足式(7)时，可得s5在左半复平面，画出系统的Nyquist曲线，如图5～图7所示。

图5 平动子系统的Nyquist曲线

此时，开环传递函数开环极点s5在左半复平面，即右半复平面只有一个极点(N=1)。而Nyquist曲线绕(-1,0)点逆时针绕了一圈。此时,Z=N-P=0，即闭环系统稳定。

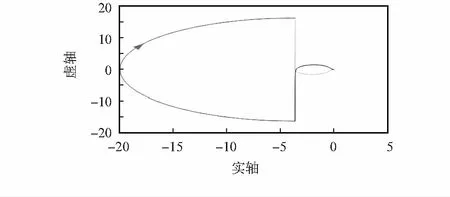
图6 转动子系统的Nyquist曲线

与平动子系统类似，转动子系统的Nyquist曲线右半复平面只有1个极点(N=1)，且曲线绕(-1,0)点逆时针绕了1圈。此时,Z=N-P=0，即闭环系统稳定。

而随着η的逐渐增大，曲线发生形变，并且绕原点顺时针转动，当η大到一定程度后，曲线不再绕(-1,0)点旋转1周，即P=0，此时,Z=N-P≠0，即闭环系统不稳定。因此参数η不能取值过大。例如，转子转速为12 000 r/min时，当η>34 745时，系统会发生失稳。η=34 745时的Nyquist曲线为图7所示。

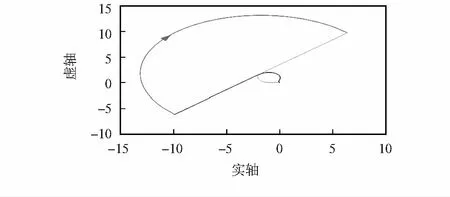
图7 η=34 745时转动子系统的Nyquist曲线

3 对含有虚数单位j的传递函数的研究

注意到T(s)有虚数单位j,故不能直接将变量重构后的系统用SIMULINK进行仿真。根据变量重构的性质，如果传递函数中出现j，则该两自由度必定存在耦合，即该系统为一个双输入双输出的耦合系统。

假设一个带有虚数单位j的传递函数为M(s)，且M(s)=A(s)+jB(s)。假设输入、输出分别为αi+jβi,αo+jβo，则

αo+jβo=(αi+jβi)·M(s)

=αi·A(s)-βi·B(s)+

j(αi·B(s)+βi·A(s))

(11)

可得

(12)

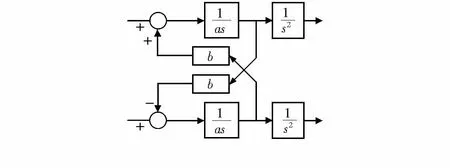
图8 L(s)等效结构

4 仿真

由于3倍频干扰在所有倍频干扰中最明显，对磁轴承控制系统的影响也最大，所以本文主要对3次谐波干扰进行研究。参数如表1。

表1 系统的参数值

4.1 平动两自由度子系统

平动两自由度子系统在转速分别为18 000，30 000 r/min时对基于同步旋转坐标陷波器和自适应陷波器的陷波效果进行仿真研究，如图9所示，其中(a1),(a2)未加陷波器,(a2)(b2)加自适应陷波器,(a3),(b3)加基于同步坐标变换的陷波器。为了滤除高频噪声，在PID控制器之前加入低通滤波器。

图9 平动子系统不同转速陷波效果对比

由图9可以看出，转速为18 000 r/min时，基于同步坐标变换的陷波器的系统收敛时间只有0.37 s左右，而自适应陷波器的收敛时间约为4.3 s，前者收敛速度为后者的11.6倍左右。转速为30 000 r/min时，前者收敛时间为0.36 s左右，后者收敛时间为4.7 s左右，前者收敛速度约为后者的13倍。