电液比例伺服系统模糊PID复合控制应用研究

2019-01-14，，，

液压与气动 2019年1期

，，，

(1.北京理工大学自动化学院，北京 100081； 2.北京市国家税务局第一稽查局，北京 100013)

引言

电液比例伺服系统是一种非线性时变系统，存在死区、摩擦和变流量增益等非线性因素，这些因素严重影响着伺服系统的控制性能。传统PID控制器对参数变化十分敏感，一旦控制环境发生变化，其控制效果将大大下降，而模糊控制则不需要关于系统变量的精确信息，因此模糊算法被大量用于电液比例伺服系统中，对比国内外学者做了大量研究。彭辉等[1]采用模糊算法调整PID控制器参数和非对称性补偿因子，形成了双模糊控制，实验结果表明，双模糊控制能够适应大范围变化负载，同时补偿非对称液压缸带来的控制非对称问题；丁问司等[2]提出了一种基于粒子群算法优化的模糊自适应PID控制方法，以模糊逻辑在线调整PID参数，以粒子群优化算法实现对模糊控制比例因子和量化因子的寻优，实现了对系统最优参数匹配下的自适应控制；PRATUMSUWAN等[3]提出了一种基于模糊逻辑的预补偿器和模糊控制器，混合模糊PID控制器的预补偿性能比较优越；FEI L[4]针对比例阀死区提出了死区自调节动态补偿方法，消除了比例阀死区引起的滞后效应，并采用自适应模糊-PD控制策略，解决了变流增益的问题。除了模糊算法，各种先进算法如迭代算法[5]、遗传算法[6]、粒子群算法[7]等也被应用到电液比例伺服系统中。

由于PID控制技术具有控制算法简单，调节方便、可靠性和稳定性好等优点，其广泛应用于工农业生产中，加之电液比例伺服系统存在大量时变非线性因素，本研究分别采用了PID算法和模糊算法对电液比例伺服系统进行了研究，分析各自控制效果，然后根据控制效果提出了模糊PID复合控制，使PID控制和模糊控制优势互补。

1 系统原理

1.1 系统组成

本研究采用的电液比例伺服系统原理如图1所示，该系统主要由控制器、比例放大器、液压缸、位移传感器等组成，相关元件的型号与技术参数已由文献[8]给出。文献[9]中指出，影响系统控制性能的两个最主要的因素分别为比例阀的中位死区和液压缸的非对称性。

图1 电液比例伺服系统原理图

1.2 比例阀中位死区

本研究采用PARK某型号比例阀，其流量特性如图2所示。从流量特性曲线可知，当输入信号U在量程的25%以内时，比例阀的阀口没有流量流出，即产生了死区。阀芯和阀口间之间的重叠量及摩擦是造成比例阀中位死区特性的最主要的两个因素[8]，比例阀因此在换向时产生时滞，系统的控制性能大为下降。

图2 比例阀死区特性

2 控制策略设计

2.1 模糊控制

模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制算法。本研究以输出e和输出变化量Δe作为模糊推理的输入，经过模糊化和模糊推理后得到模糊化后的输出ΔU，解模糊化得到实际的控制量u，模糊算法设计原理如图3所示。

图3 模糊算法设计原理

在进行模糊化处理时，e,Δe和控制变量u的模糊论域选取正大、正中、正小、零、负小、负中、负大(PB，PM，PS，ZO，NS，NM，NB)7个语言变量值档次，取输入变量e和Δe的论域为[-5,5]，输出变量u的论域为[-3,3]。e和Δe，u的隶属度函数分别如图4、图5所示，模糊控制规则如表1所示。

图4 输入变量e和Δe的隶属度函数

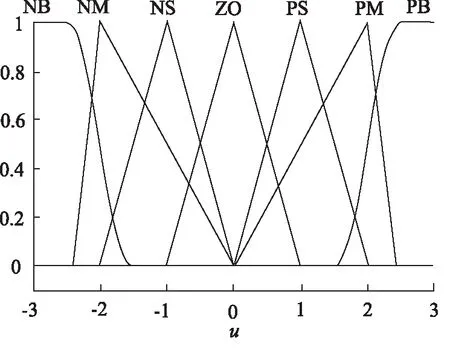
图5 输出变量u的隶属度函数

表1 模糊控制规则

2.2 模糊PID复合控制算法设计

模糊控制和传统的PID控制单独使用都不能很好地解决系统的非线性问题，对此，本研究将模糊控制与传统PID控制算法相结合，设计了模糊PID复合控制。其基本思路为：

设置一个“软”自动切换开关S，通过偏差预设定的“阈值ε”比较结果来决定两种控制方式选择。

当|e|≥ε时，认为系统运行在动态过程，应采用模糊控制方式,发挥其动态性能好、超调量小的特点。

当|e|<ε时，认为系统进入到了稳态，应切换为PID控制方式，发挥其稳态精度高的优点，减小稳态误差。

阈值ε通过反复试验整定得到，模糊PID复合控制原理如图6所示。

图6 模糊PID复合控制的结构图

3 实验结果分析

实验平台搭建如图7所示。

3.1 PID控制

本研究中，实际控制系统的输出为位移传感器的位置信息，输入为比例放大器的电压，e和Δe的论域为[-250,250]，u的论域为[-10000,10000]。其中ke为偏差e的量化因子，kec为偏差变化率Δe的量化因子，ku为比例控制量u的比例因子。

实验采用的阶跃信号的幅值为150 mm，正弦信号的幅值为100 mm。实线曲线代表给定信号，虚线曲线代表实际采集的信号。采用传统PID控制时，当Kp=4.5,Ki=0,Kd=0.01时,实验得到的阶跃响应和正弦跟踪实验结果分别如图8、图9所示。

图7 电液比例伺服系统实验平台

图8 PID控制下的阶跃响应曲线

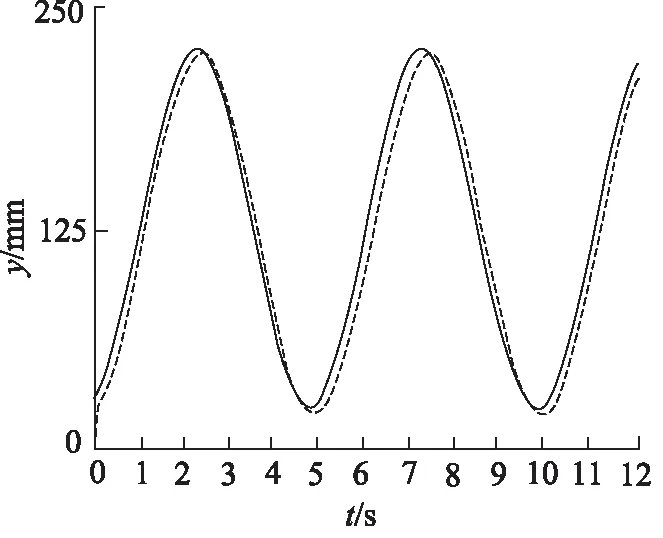
图9 PID控制下的正弦响应曲线

因为在液压缸推导模型中已经存在积分环节，为防止引入积分造成系统振荡，所以积分系数为0[8]。阶跃响应时，系统的调整时间Ts=0.35 s，超调量为2.2%，正弦跟踪时系统最终稳定在150 mm，稳态误差为0，消除了稳态误差。系统最大的跟踪误差为4.5 mm，最大的延迟时间为0.21 s，液压缸正向运动时滞后比较明显。

3.2 模糊控制

不断调整量化因子，当ke为1/50，kec为1/50，ku为10000/3时，系统的阶跃响应和正弦跟踪实验结果如图10、图11所示。

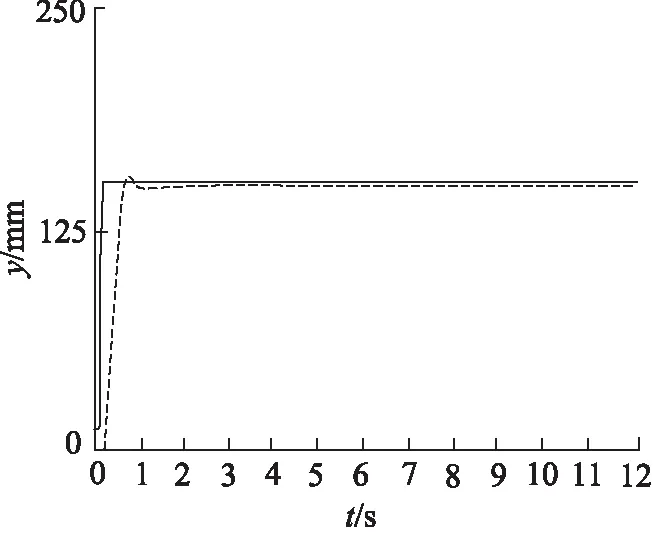
图10 模糊控制下的阶跃响应

图11 模糊控制下的正弦响应曲线

在模糊控制下，由图10可知，系统动态响应较为迅速，Ts为0.3 s，并在出现一次较小的超调后趋于稳定，超调量约为2%,最终稳定在149.7 mm处。由图11可知，系统最大的跟踪误差为3 mm，最大的延迟时间为0.19 s。图8和图10对比可知，超调量大体相等时，模糊控制可以提高系统的响应速度，但并不能消除稳态误差，正弦跟踪时，系统跟踪误差较大。

3.3 模糊PID复合控制

将阈值ε设置为7.5 mm，即当偏差大于等于7.5 mm时，系统切换为模糊控制，当偏差小于7.5 mm,系统切换为传统PID控制。当ke为3/125，kec为3/125，ku为10000/3时，系统的阶跃响应和正弦跟踪结果如图12、图13所示。

在模糊PID复合控制下，从图12可以看出，系统的阶跃响应迅速，Ts为0.3 s，并且几乎无超调，稳态误差为0。由图13可知，系统最大的跟踪误差为2.5 mm，最大的延迟时间为0.15 s。和传统PID控制和模糊控制相比，模糊PID复合控制下系统跟踪误差减小，延迟时间缩短，系统跟踪的非对称性也大大下降。

图12 模糊PID复合控制下的阶跃响应曲线

图13 模糊PID复合控制下正弦跟踪曲线

3.4 模糊PID复合控制对频率和负载的适应性分析

复合控制下，采用正弦跟踪信号，改变频率和负载，得到的实验结果如图14～图16所示。

图14 0.2 Hz 空载

图15 0.25 Hz 空载

图16 0.2 Hz 10 kg负载

由图14～图15可知，对0.2 Hz的正弦信号，实际跟踪曲线和设定曲线基本重合。对0.25 Hz的正弦信号，实际跟踪曲线有一定跟踪误差，其中最大的跟踪误差为3.2 mm，最大的延迟时间为0.2 s，但响应曲线整体没有发生失真。故模糊PID复合控制器对0.2～0.25 Hz之间的正弦信号都有很好的跟踪效果，可以适应信号频率的变化。

在10 kg负载的情况下，实际曲线和设定曲线基本重合，系统最大的跟踪误差为3 mm，最大延迟时间为0.2 s，和空载情况下的控制效果相比，系统的抖动反而更小了。