基于移动热边界的动涡旋盘温度场有限元分析

2019-01-14，，

液压与气动 2019年1期

，，

(1.南昌大学机电工程学院，江西南昌 330031； 2.上海机电工程研究所，上海 201109)

引言

涡旋压缩机由于其节能静音、结构紧凑等诸多优点被广泛应用于空调制冷及气体压缩。涡旋压缩机是一种依靠动涡旋盘的偏心平动与静涡旋盘啮合来实现气体压缩的流体机械。由于气体压缩带来的涡旋盘的温度变化，使得动静涡旋盘产生热变形，从而影响动静涡旋盘之间的正常啮合使压缩机失效，因此很多学者对涡旋盘的温度场进行了研究。

由于动涡旋盘的温度场无法直接测量得到，因此多采用有限元方法进行数值模拟。为了获得动涡旋盘的温度场，首先需要对涡旋压缩机的换热过程进行计算。JANG K[1]通过实验对制冷涡旋压缩机内部的对流换热进行了研究，并建立了传热相关性计算式；王俊亭[2]将Gnielinski公式用于无油空气涡旋压缩机的换热过程计算，并进行了相关实验验证；PEREIRA E L L[3]建立一个更通用的压缩腔内对流换热的预测模型；在进行动涡旋盘的温度场数值模拟时，李超和刘国平[4-5]将动涡旋齿的温度分布简化为与涡旋盘半径呈线性关系；殷俊和羊玢[6-7]将动涡旋齿的温度分布简化为与涡旋线展角呈线性关系；LIN C、LIU Y和YANG Y等[8-10]对涡旋盘特定位置施加温度边界条件进行稳态热分析，得到涡旋盘的温度场。

目前对于压缩机压缩腔内的对流换热研究已有较多成果，但进行涡旋盘温度场分析时，却将其温度边界条件过于简化。实际上根据涡旋压缩机的运行特点可以知道涡旋盘上的热边界条件是呈现周期性变化的。涡旋盘上的温度并不是简单的稳定加热过程，而是随着涡旋盘瞬时温度及热边界条件的变化，相应地被加热或冷却，因此为了得到更符合实际的涡旋盘温度场，介绍了一种基于动态热边界的动涡旋盘温度场有限元分析方法。

1 涡旋压缩机涡旋盘热载荷特性分析

在进行温度场有限元分析时，需要确定好其热边界条件，因此先对涡旋压缩机的热载荷特性进行分析。动涡旋盘上的热量主要来自压缩气体与涡旋盘表面的对流换热。涡旋压缩机在工作过程中，任意时刻都存在着多组封闭的月牙形工作腔，随着主轴转动，各组工作腔由外向内连续移动。工作腔容积逐渐由大变小，工作腔内的温度及对流换热系数逐渐从小变大，主轴每转动一周，工作腔完成一个周期的变化。在进行工作腔内的热力计算时，通常假设工作腔内的气体状态参数相同[11]。基于这一假设，任意工作腔内的热边界载荷也是相同的。此外，由于涡旋压缩机的工作特性，在涡旋齿头处会存在一部分涡旋齿始终处于排气状态；在涡旋齿尾处，会有一部分涡旋齿始终处于吸气状态。

2 仿真前处理

2.1 涡旋盘建模及网格划分

首先根据涡旋盘参数进行涡旋盘的建模，本研究涡旋压缩机运行工况及涡旋盘参数如表1所示。

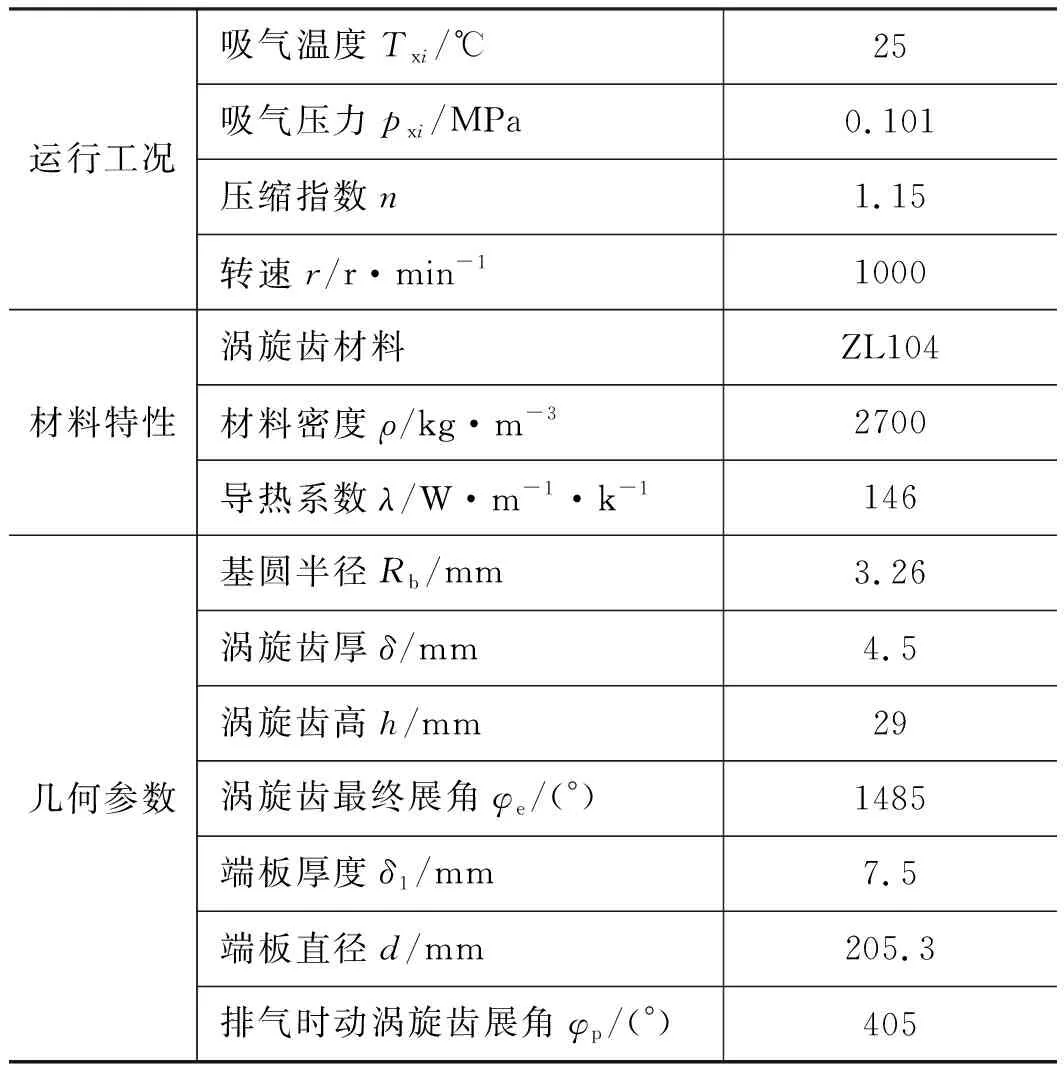
表1 动涡旋盘参数

在涡旋齿建模的过程中，为方便后续实现动载荷的施加，将涡旋齿及涡旋盘端板面分割成多个子面。由于涡旋盘上压缩腔在周期变化的过程中，相同时间内，对应的涡旋齿转过的角度是相同的，因此，每隔相同角度φ进行涡旋面及涡旋盘端板面的划分，并形成如图1所示的多个展角度数相同的子涡旋面和子端板面。当子面划分的越多，其热载荷条件与压缩机实际运行工况就越符合。

图1 涡旋盘表面划分情况图

涡旋盘进行网格划分时，单元材料属性根据表1中的材料特性进行定义，采用四面体网格划分方式，网格单元尺寸设为1 mm。

2.2 热边界载荷计算

由于涡旋盘主要通过其与压缩气体接触的表面以对流换热的形式进行热交换，在对涡旋盘上的边界进行热力计算时作出以下假设[12]：

(1) 假定任意压缩腔内气体的状态参数相同；

(2) 仅考虑与压缩腔内气体接触的涡旋盘表面的对流换热，则对于涡旋盘上其他表面可视为绝热处理。

对流换热边界包括温度及对流换热系数的计算。假设压缩机完成一次压缩的过程中主轴的转角为θ，则压缩腔内气体温度可表达为随转角θ变化的函数:

(1)

式中，Tθ——压缩腔内气体温度

Txi——吸气温度

Vxi——吸气容积

n——压缩指数

Tp——排气温度

θp——排气时对应的主轴转角

φe——涡旋线最终展角

压缩腔内对流换热系数同样可表达为随转角θ变化的函数[2-3]：

(2)

式中，hθ——压缩腔内对流换热系数

Ror——转动半径

r——转速

vθ——压缩腔内气体速度

Dθ——压缩腔当量直径

Dc——压缩腔平均曲率直径

λa——空气导热系数

Re——雷诺数

Pr——普朗特数

其中:

(3)

(4)

式中，A1θ——压缩腔底面面积

A2θ——内涡旋面面积

A3θ——外涡旋面面积

pxi——吸气压力

M——空气摩尔质量，约为0.029 kg/mol

B——与气体种类有关的常数,空气为110.4 K

μ0——15 ℃时气体的动力黏度,其大小为 1.7894e-5

根据涡旋压缩机基本参数，结合以上计算公式得到不同转角θ下压缩腔内气体温度T及对流换热系数h分别如图2、图3所示。

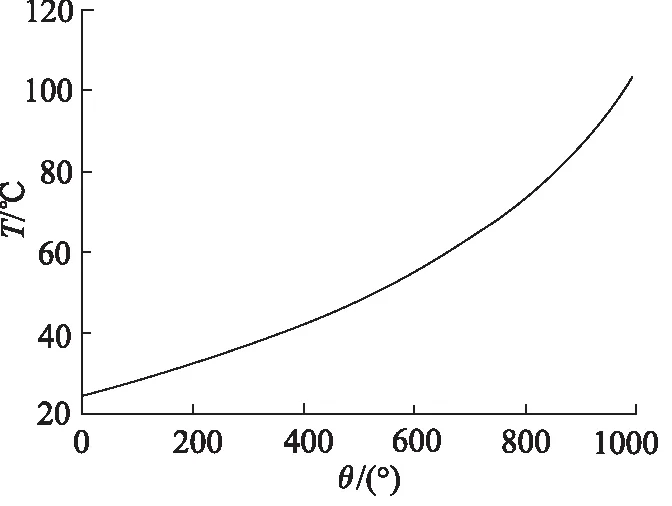
图2 压缩腔内气体温度变化图

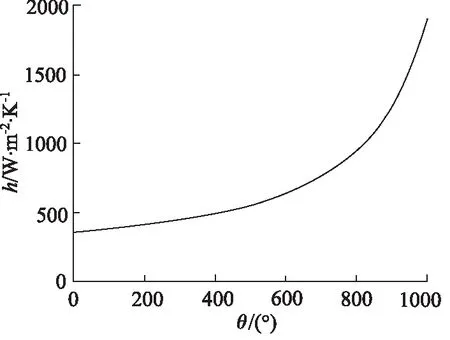
图3 压缩腔内气体对流换热系数变化图

在转动一周内，本研究的涡旋盘各压缩腔的温度及对流换热系数的变化如下：

i为压缩机吸气开始，主轴在转动一周过程中所处的角度，i∈[0,360°]。

第一压缩腔：

Ti=Tθ；hi=hθ，此时θ=i；

第二压缩腔：

Ti=Tθ；hi=hθ，此时θ=i+360°；

第三压缩腔：

Ti=Tθ；hi=hθ，此时θ=i+720°。

2.3 各载荷步载荷的施加

现以内涡旋面为例，简要介绍其载荷施加的过程。如图4所示，假设φ为45°，则由外向内，其涡旋面的序号分别为1,2,3，…,33,每一圈所包含的涡旋面个数为8。同时，由排气展角为405°可知，当涡旋齿啮合点处于面号24后，中心压缩腔开始排气。假设主轴转角为0°时为第一个载荷步，动静涡旋盘处于如图5所示的吸气状态，此时涡旋面25,26，…，33处于排气腔，17,18,…，24处于第一压缩腔，9,10，…，16处于第二压缩腔，1,2，…，8处于第三压缩腔。当主轴转角转过φ，如图4所示，此时为第二个载荷步，第三压缩腔序号变为2,3，…，9，第二压缩腔序号变为10,11，…，17，第一压缩腔序号变为18,19,…，25，排气腔序号变为26,27，…，33。当主轴转角为N·φ时，此时为第N-1个载荷步，第三压缩腔的面序号为N-(N-1+8),第二压缩腔的面序号为(N+8)-(N-1+8·2)，第一压缩腔序号变为(N+8·2)-(N-1+8·3)，排气腔为(N+8·3)，…，33。面序号1-N由于没有形成封闭的压缩腔，其涡旋面上气体状态与吸气状态相同，因此当成吸气腔来处理。综上可以通过对各子涡旋面的序号操作来实现动态边界的拾取。拾取边界后，在各边界上施加与之相对应的对流边界条件即可。同理，可以利用相同的方法进行涡旋盘外涡旋面及端板面载荷的施加。需要注意的是，对于部分端板面上其流体状态处于两级压缩腔的混合状态的情况，取这两级气体的对流换热的平均值为其面上的等价对流换热，而对于涡旋盘上的其他部分面，由于与外界的热量交换较少，当成绝热条件处理。

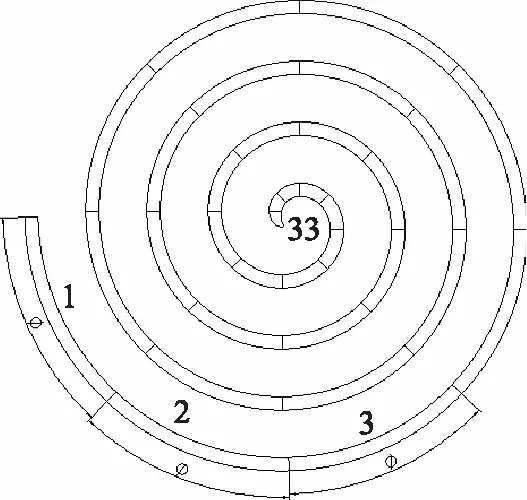
图4 涡旋盘壁面各子面序号分布图

图5 涡旋齿不同时刻啮合图

3 仿真结果与分析

3.1 不同时刻涡旋盘温度场分布情况

将热分析的求解类型设置为瞬态热分析，并定义好初始温度、子步数等，进行各子步的叠加求解后得到涡旋盘的瞬态温度场，根据涡旋盘温度场随时间变化的特点分别提取10，50，100,200 s时的温度分布云图分别如图6所示。

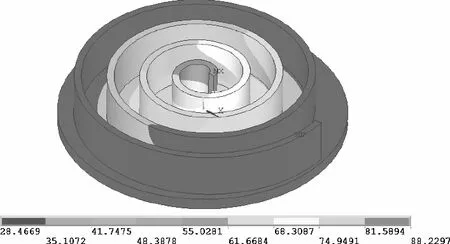
a) 10 s时

b) 50 s时

c) 100 s时

d) 200 s时图6 随时间变化温度分布云图

从上图中可以看出，在压缩过程中，涡旋盘的温度是由中心开始逐渐向周边扩散的。为了解涡旋盘上各个位置温度的变化历程，从涡旋齿尾开始，每隔展角π分别提取涡旋齿顶及齿底的节点在200 s内的温度变化曲线如图7所示。

a) 齿顶

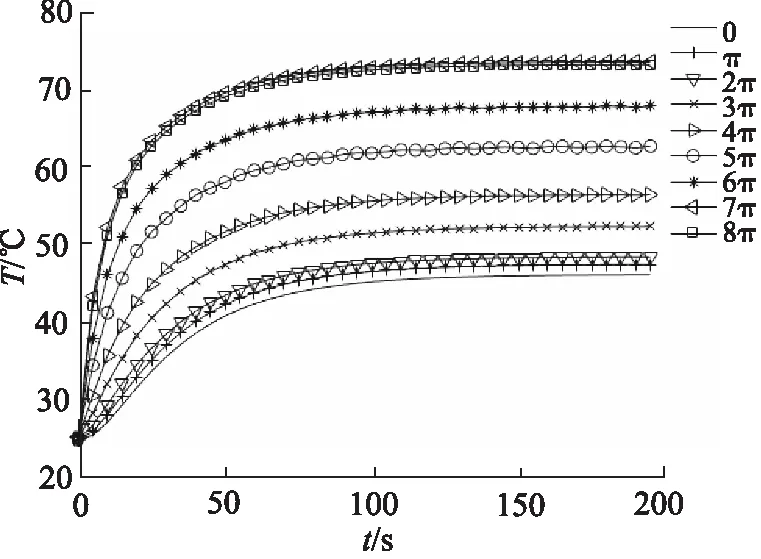
b) 齿底图7 涡旋温度变化曲线

从图中可以看出，无论涡旋齿顶部还是底部，在受热初期，涡旋盘上的温度变化都十分明显，表现为快速增长的趋势，随后温度变化逐渐趋于平缓。同时可以发现涡旋齿顶部温度变化明显要大于底部，且越是远离齿尾，涡旋齿的温升速率越快。在大约150 s时，涡旋齿温度基本不再发生变化，在200 s时，涡旋齿温度基本可以认为不再发生变化。

3.2 趋于稳定时涡旋盘温度分布情况

为了解涡旋盘温度在趋于稳定时，其温度场的分布情况，从涡旋齿尾开始，每隔展角π分别提取内涡旋齿顶及齿底在200 s时的温度。设φ为距涡旋齿尾的展角弧度，得到涡旋齿上温度T随φ变化的温度分布情况如图8所示。

从图中可以看出，涡旋齿顶和齿底的温度都是呈由齿尾向齿头逐渐增大的趋势，而在齿高方向，从齿尾开始，涡旋齿上的温差逐渐减小至0，随后又逐渐增大。同时可以发现，两条温度分布曲线存在一个交点，这说明，在涡旋齿某一位置处，涡旋齿高方向温差趋近于0，并且在此位置处的两侧，涡旋齿高度方向温差呈现两种相反的变化趋势。