环境温度对圆拱形钢结构模态频率的影响研究
2019-01-14刘 哲,丁 阳,2,宗 亮,2
刘 哲,丁 阳, 2,宗 亮, 2
环境温度对圆拱形钢结构模态频率的影响研究
刘 哲1,丁 阳1, 2,宗 亮1, 2
(1. 天津大学建筑工程学院,天津 300072;2. 滨海土木工程结构与安全教育部重点实验室(天津大学),天津 300072)
为研究圆拱形钢结构模态频率在环境温度下的时变特征,本文以潍坊市白浪河摩天轮钢结构为研究对象,首先采用数值模拟和实测数据统计分析的方法揭示其模态频率的温度影响规律,然后采用BP神经网络建立起该结构模态频率与环境温度之间的回归模型,并基于该模型消除环境温度对结构模态频率的影响.结果表明:环境温度主要通过使结构材料的力学性能和结构状态发生改变来影响圆拱钢结构的模态频率;白浪河摩天轮结构模态频率随温度升高而降低,在监测时间内频率最大变化幅度为3.04%;该结构面内振型频率所受温度影响高于面外振型,其中结构状态改变是面内振型频率变化的主要因素;BP神经网络模型可以正确反映模态频率和环境温度之间的变化关系,利用建立的频率-温度回归模型可有效消除环境温度对结构模态频率的影响.
环境温度;圆拱形钢结构;模态频率;BP神经网络
在结构健康监测领域,模态频率能反映整体结构动力特性的变化,已成为结构安全评估及损伤识别中最常用的指标.然而,研究发现[1-2]环境温度变化会引起结构模态频率的波动,甚至可能淹没轻微损伤所带来的频率变化,从而使得结构安全评估难以实现.因此,分析环境温度对结构模态频率的影响规律并消除实测数据中夹杂的温度影响,得到反映结构本身状态微小改变的真实模态频率,是结构健康监测中的关键问题.
目前许多学者分析了环境温度对结构模态频率的影响.Sohn等[3]对Alamosa Canyon桥的第1阶模态频率进行监测,发现其在24h内的变化幅度可达5%;监测数据表明在环境温度作用下水立方[4]和广州塔[5]的模态频率波动范围分别为3%和7%;王立新等[6]采用支持向量机(SVM)对珠江黄埔大桥监测数据进行建模分析,发现模态频率随环境温度的升高而减小.现有研究大多以梁式结构体系为研究对象,然而不同的结构形式其模态频率受温度的影响差别很大[7].圆拱形钢结构作为一种特殊的结构形式,其振型位移为空间6自由度且结构状态随温度的变化与梁式结构有很大不同,以梁式体系为研究对象所得的频率-温度影响规律并不适用.因此,有必要开展圆拱形钢结构模态频率的温度影响研究.
针对以上问题,本文首先对圆拱形结构模态频率的温度影响进行分析;然后以潍坊市白浪河摩天轮钢结构为研究对象,采用数值模拟和实际监测数据统计分析的方法揭示温度作用下圆拱形钢结构模态频率的变化规律;继而采用BP神经网络技术建立起模态频率与环境温度之间的回归模型,并基于该模型消除环境温度对其模态频率的影响.研究成果可为环境温度下圆拱形钢结构的温度效应和安全评估研究提供参考.
1 圆拱形钢结构模态频率的温度影响分析
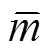
为了分析温度改变对结构自振频率的影响,假定拱梁结构阶无阻尼振动频率的计算公式[8-9]为

(1)

(2)

(3)
将式(1)、(2)分别代入式(3),整理可得
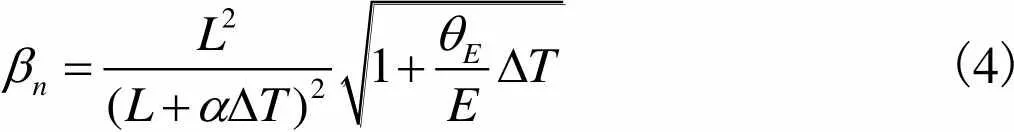
(4)
由以上温度对拱梁模态频率影响的初步分析可知,温度对拱形钢结构模态频率影响是由于变温使弹性模量和结构状态发生改变所致.拱形结构约束形式不同,其内力和几何状态的改变也不同.在温度改变时,既可能产生拉力也可能产生压力,因此应根据实际结构形式进行具体分析.大型圆拱形钢结构模态频率的解析解通常很难推导,在进行实际工程分析时可采用数值模拟的方法,从而量化温度变化对模态频率的影响.
2 圆拱形钢结构模态频率的温度影响研究
2.1 工程概况及有限元模型
白浪河摩天轮[10]坐落于潍坊市白浪河大桥中央,是采用编织网格形式的无轴式摩天轮,其俯视图如图2(a)所示.摩天轮外轮廓直径为125m,其轮盘结构是一个由网状编织网格所形成的圆拱形钢结构.圆拱通过下部斜柱和两侧拉索与基础相连形成支撑体系.摩天轮轿厢沿设置在固定轮盘上的轨道旋转.该结构体型新颖、结构复杂,每根杆件皆存在角度不同的空间扭转.结构构件均暴露在大气中,所受温度作用显著.
采用有限元软件ANSYS建立摩天轮结构的有限元模型,如图2(b)所示.模型中拉索采用Link10单元模拟,其拉力通过施加初应变来实现.钢管构件采用Beam188单元模拟,轨道轿厢等采用Mass21单元模拟.模态分析时采用Block-Lanczos法,并以自重作用分析终态作为模态分析的初始状态.结构前100阶的频率分布如图3(a)所示,从图中可以看出该结构模态频率非常密集,其基频为0.445Hz.结构前4阶振型如图3(b)~3(d)所示,分别为面外1阶弯曲、面内1阶侧弯、面外2阶弯曲和面内1阶竖弯.
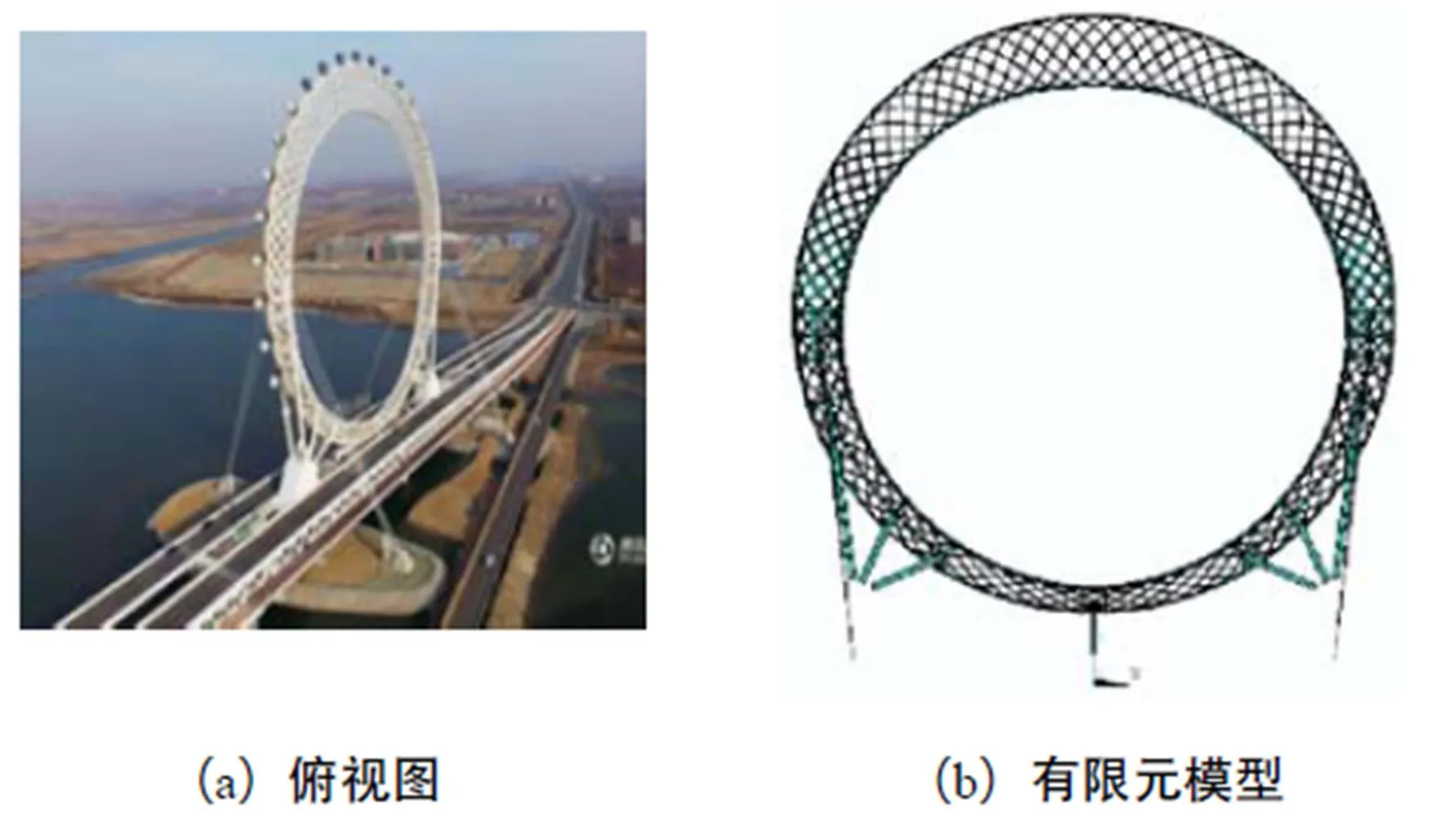
图2 白浪河摩天轮
2.2 温度影响模态频率变化的数值研究
目前,在进行钢结构设计时一般不考虑环境温度改变所引起的弹性模量变化,即在环境温度下假定钢结构的弹性模量不变.然而由环境温度对圆拱形钢结构模态频率的影响分析可知,温度影响圆拱形结构模态频率主要有以下两种方式:一是材料弹性模量改变;二是结构内力和几何状态改变.为了分析以上两种影响因素对结构模态频率影响的大小,下面将从这两方面分别进行研究.
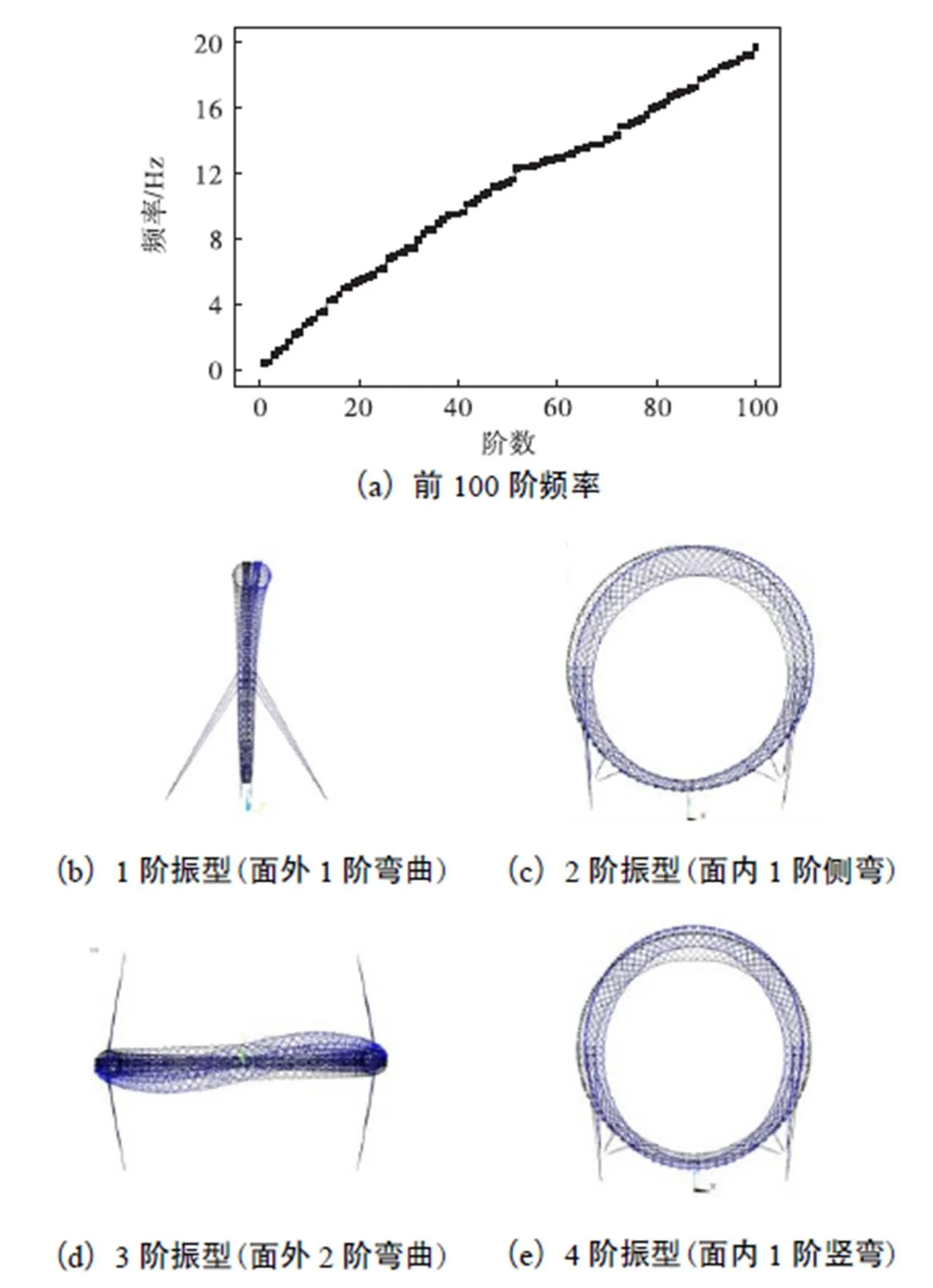
图3 白浪河摩天轮模态信息
2.2.1 弹性模量改变对频率的影响
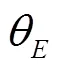

(5)
式中:20为20℃时的结构模态频率;f为温度时的结构模态频率.
由图4(b)可知,在计算温度范围内,前4阶结构模态频率随温度的升高而降低.弹性模量改变导致的摩天轮结构前4阶模态频率的变化范围在-1.0%~1.0%之间,其中面内和面外振型的模态频率变化率相差不大.由于在弹性模量变化的同时,结构内力状态也会发生变化,从而对模态频率造成影响.本文对结构典型杆件的内力进行了分析,如图5所示.由图5可知,弹性模量改变对结构典型杆件内力影响很小,因此可以忽略因弹性模量改变造成的内力状态改变而影响的频率变化.
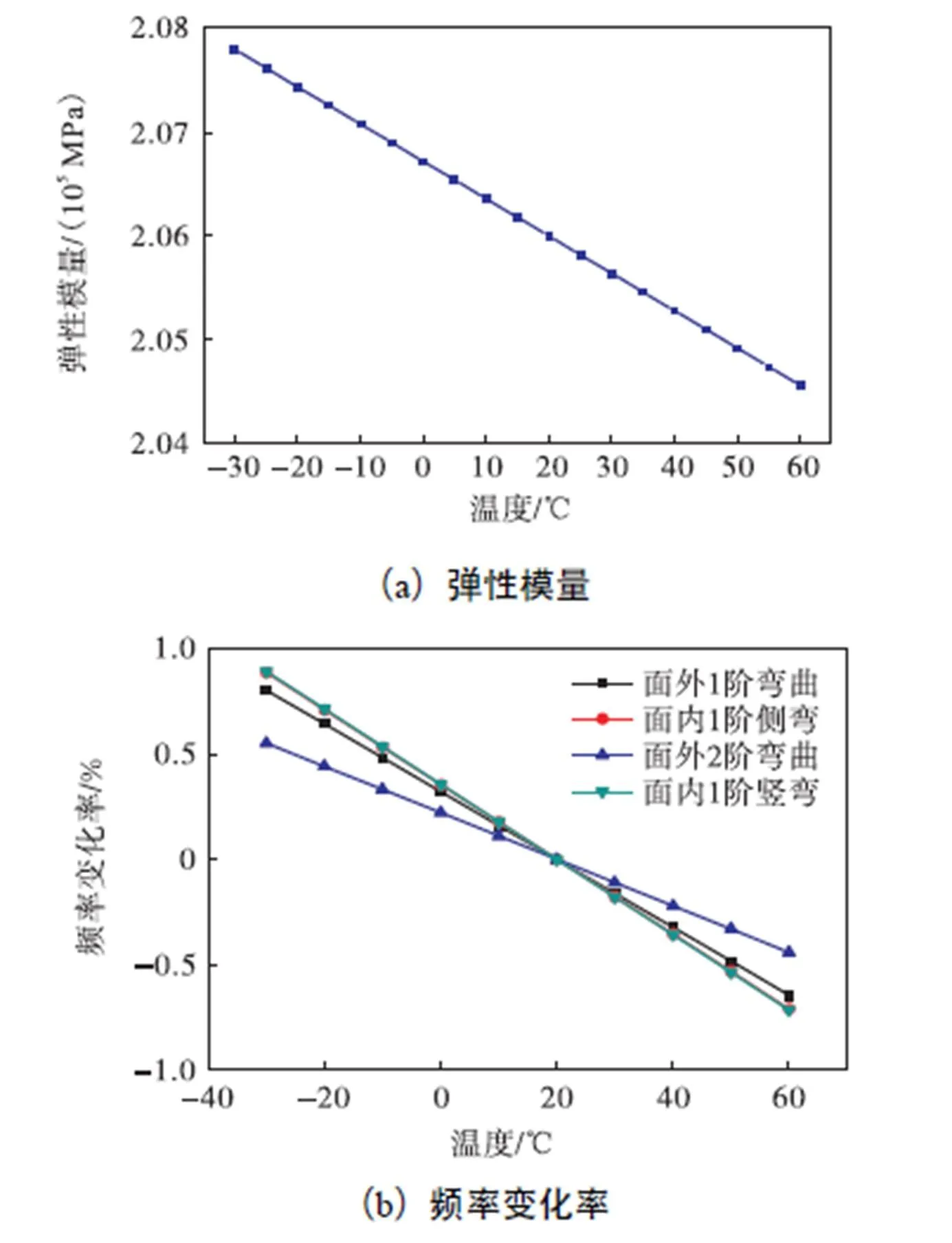
图4 弹性模量、频率变化率随温度的变化情况
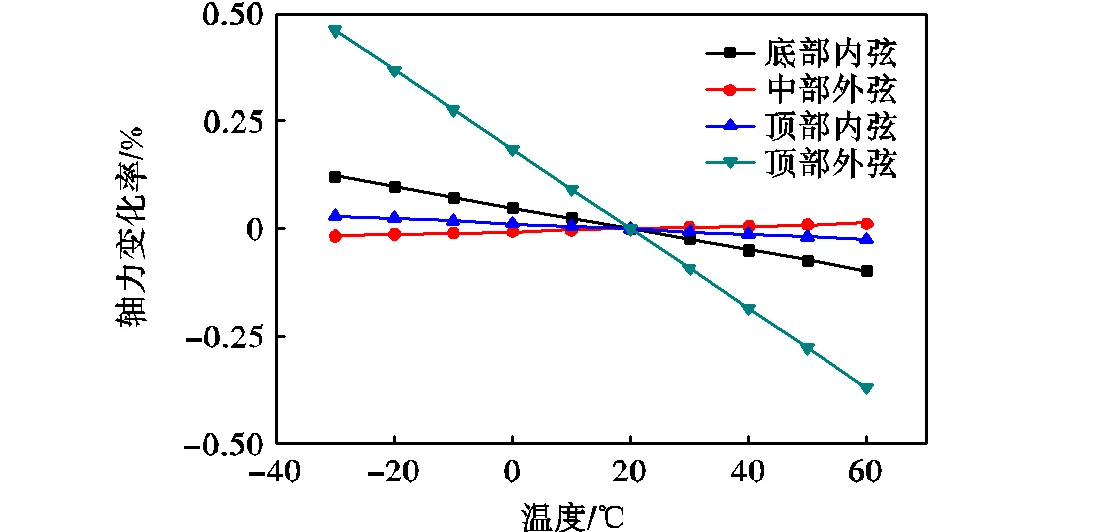
图5 典型杆件的内力变化
2.2.2 结构状态改变对频率的影响
假定材料弹性模量不变,研究温度变化造成的结构状态改变对模态频率的影响.首先以20℃为参考温度进行不同温度下的静力计算,然后以计算后的状态作为初始状态进行模态分析.图6为不同温度下结构内力和几何状态改变所引起的频率变化率曲线.
由图6可知,在计算温度范围内,前4阶频率与温度呈现不同的比例关系.面外1阶和面外2阶振型频率的变化范围在-0.06%~0.06%之间,远小于弹性模量改变引起的频率变化,因此在温度影响分析时可忽略结构状态改变所引起面外振型的频率变化.结构面内振型频率随温度的升高而降低,在计算温度范围内,面内1阶侧弯和面内1阶竖弯的频率变化率分别为1.03%和1.45%,明显高于弹性模量改变引起的频率变化.下面给出了不同温度下结构状态的变化情况.图7(a)和图7(b)分别为60℃时杆件应力变化值和结构位移云图,图7(c)和7(d)分别为 -30℃时杆件的应力变化值和结构位移云图.
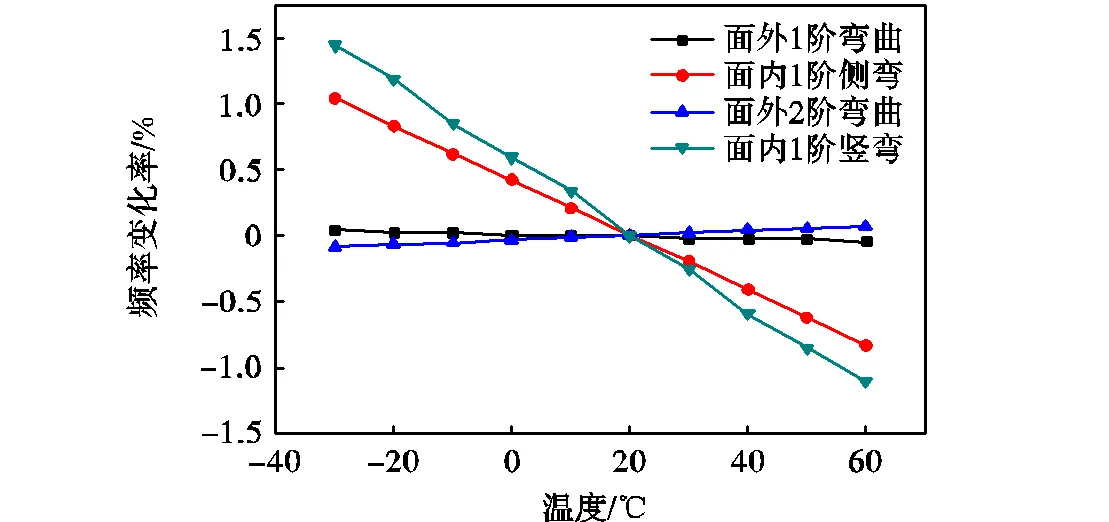
图6 频率变化率与温度的关系
从图7中可以看出,温度升高时摩天轮结构膨胀,最大变形为72mm,发生在结构两侧位置处;温度降低时结构收缩,最大变形为177mm,发生在结构顶部内弦位置处.升温时大部分杆件呈受压趋势,降温时大部分杆件呈受拉趋势.在计算温度范围内,温度每变化10℃,大部分杆件应力变化约为1MPa.可见,在不考虑温度引起的弹性模量变化时,结构面内振型频率与温度成反比.
综合数值模拟结果可知,白浪河摩天轮结构模态频率随温度升高而降低.在环境温度作用下,结构面外振型频率改变主要由弹性模量改变所致,而面内振型频率改变主要由结构状态改变所致,且面内振型频率的温度敏感性高于面外振型频率.在计算温度范围内,面内1阶竖弯模态频率的变化幅度最大,在 -2.5%~2.5%之间.
2.3 温度影响模态频率变化的实测数据分析
2.3.1 模态参数识别
采用三向加速度传感器(见图8(a))测量该结构的动力特性,测点布置如图8(b)所示.温度数据的采样频率为每小时一次.采集时间内风速均低于4m/s,此时风速对结构模态频率的影响可忽略不 计[12].加速度数据采样频率为50Hz,典型加速度时程如图9(a)所示.采用峰值法对该结构进行模态参数识别,即取自功率谱密度图上的峰值作为结构的模态频率.经频谱变换后的数据如图9(b)所示.
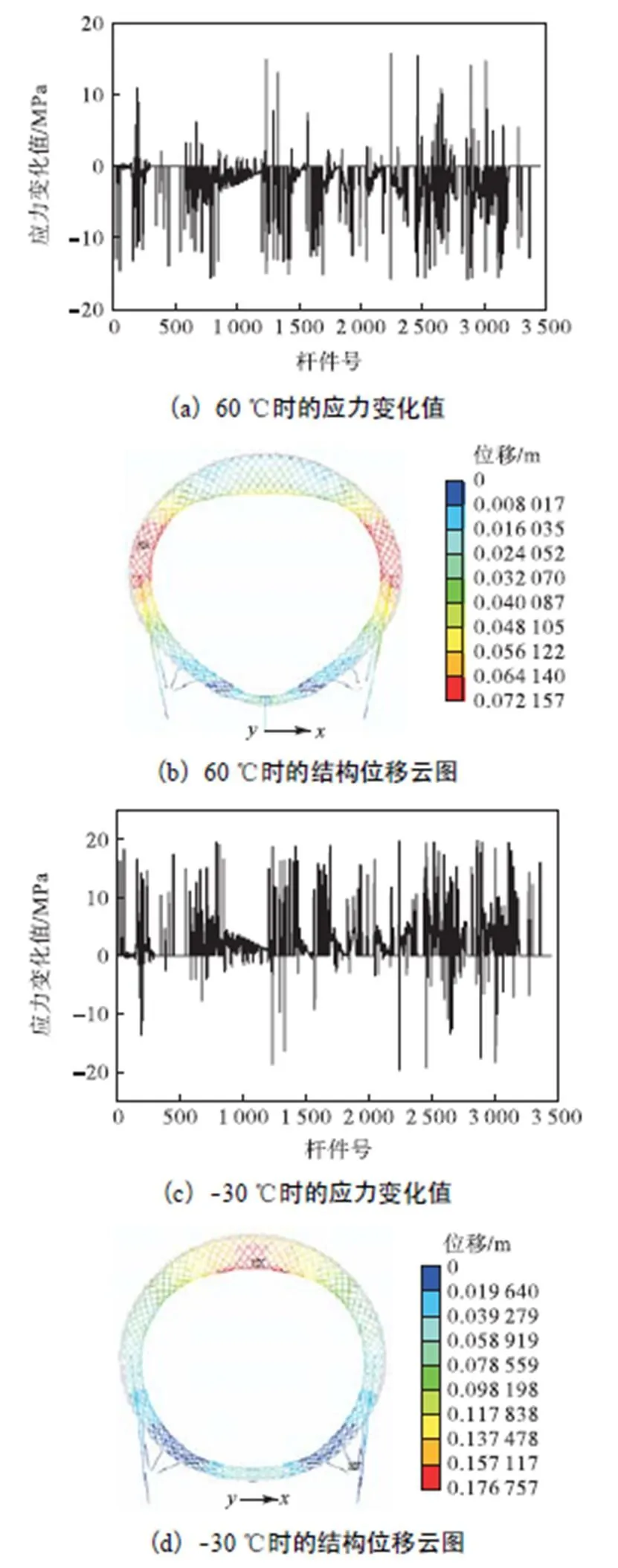
图7 结构内力和位移的变化
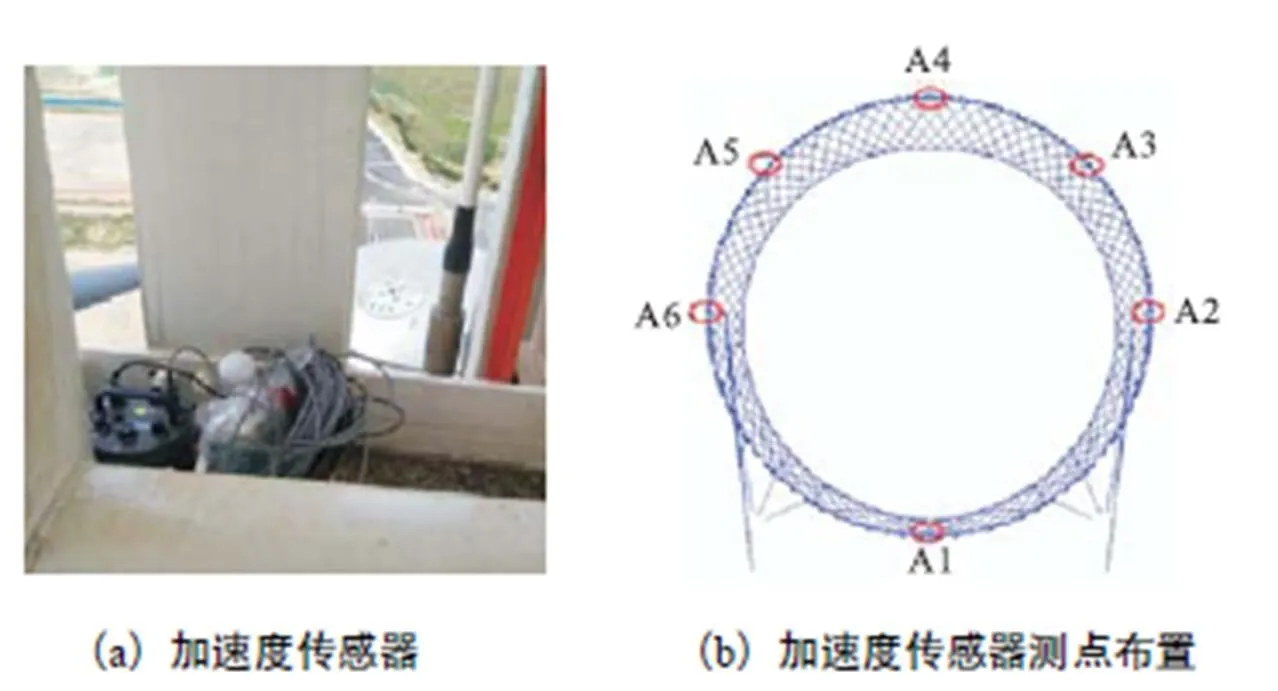
图8 加速度传感器布置
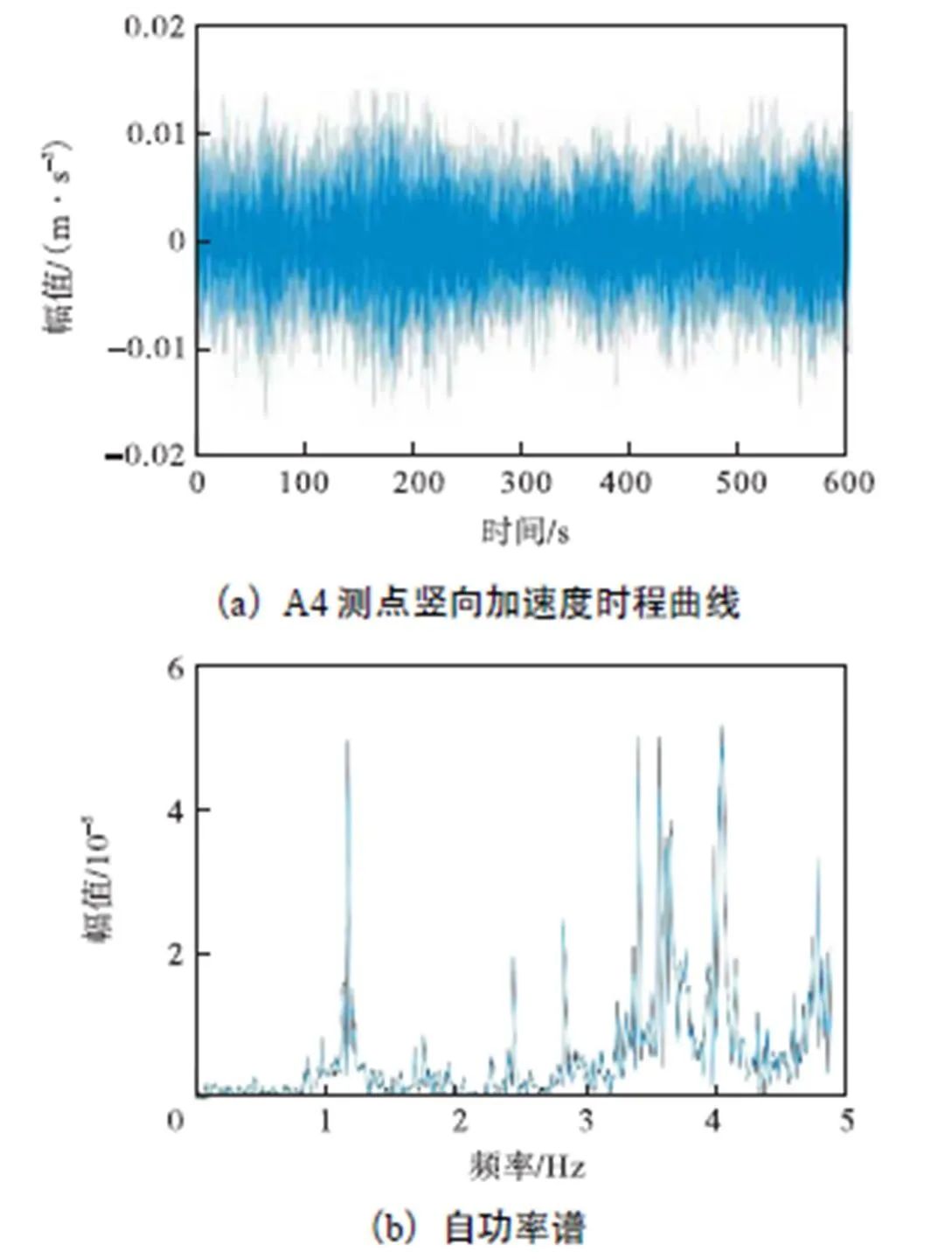
图9 A4测点竖向加速度信号频谱分析(2017-06-30,06:00—06:10,20℃)
表1为摩天轮结构在温度为20℃时识别的前4阶模态频率与计算值的比较,可知采用峰值法能够识别结构主要模态的频率,误差均小于3%.实测结果可用于下一步模态频率与环境温度的相关性分析.
表1 模态频率识别结果
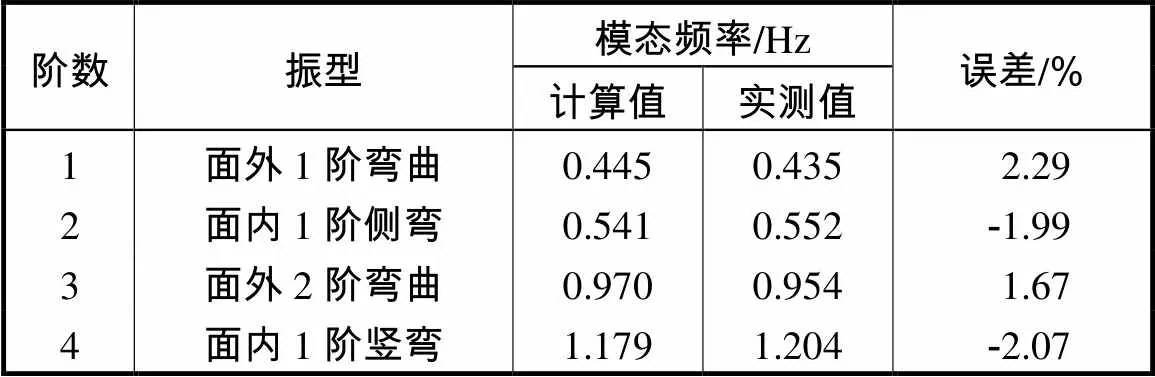
Tab.1 Identification results of modal frequency
2.3.2 频率与温度的相关性分析
对2017年6月30日00:00到7月6日00:00连续168h采集的数据进行统计分析,从而研究摩天轮结构模态频率与环境温度之间的关系.对每小时采集的数据进行一次模态识别,并对识别结果采用最小二乘法进行线性回归拟合.结构前4阶频率的拟合结果如图10所示,表2为模态频率识别结果与环境温度的相关性分析.
由图10可以看出,结构实测模态频率与环境温度呈负相关,其大小随着温度的升高而降低.由表2可知,面内1阶侧弯频率和面内1阶竖弯频率的方差明显大于面外振型频率的方差,说明面内振型频率受温度影响较大,这与数值模拟分析一致.在监测时间范围内,前4阶模态频率分别变化了1.85%、2.94%、1.27%和3.04%.由计算可知,当结构整体刚度下降5%时,面内1阶竖弯振型频率变化为1.3%.可见,该结构环境温度改变导致的频率变化足以将轻微损伤造成的频率变化掩盖,因此在以模态频率为损伤指标进行安全评估时必须消除环境温度的影响.
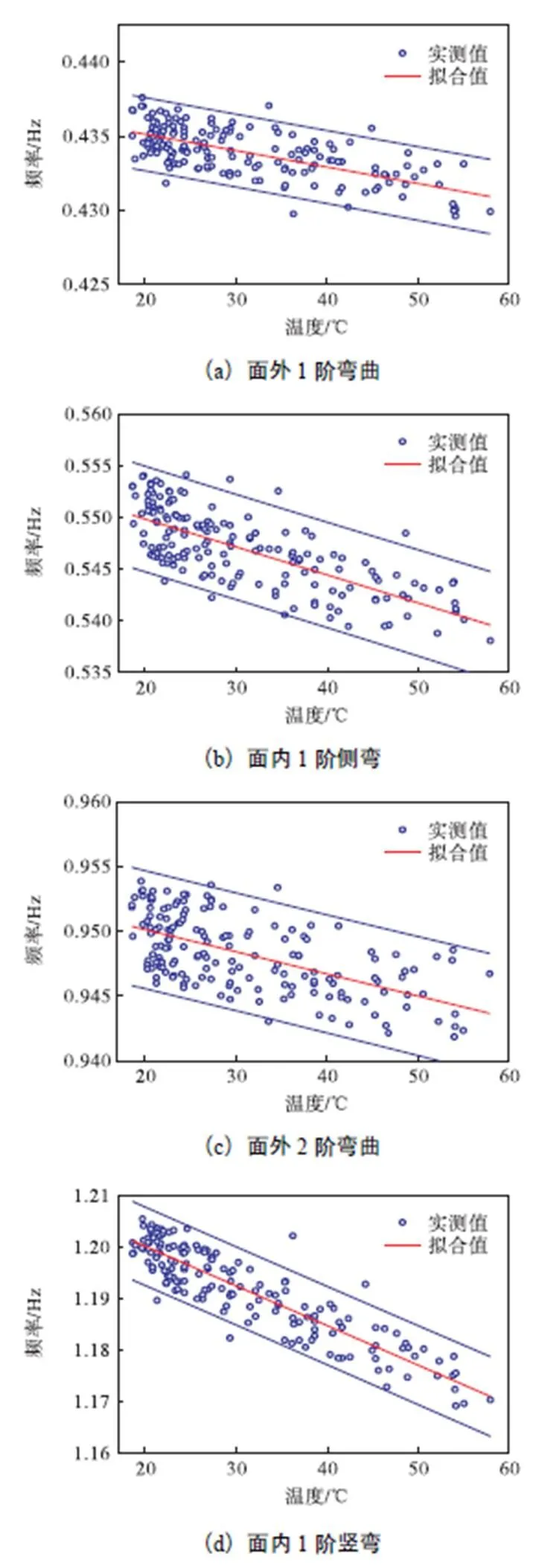
图10 模态频率与温度的关系
表2 模态频率与温度相关性分析
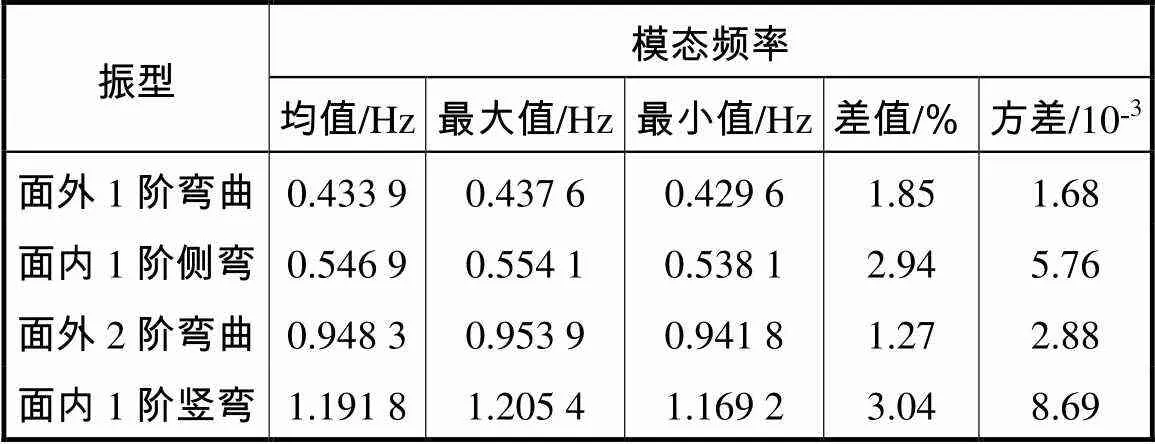
Tab.2 Correlation analysisbetween modal frequency and tem-perature
3 模态频率温度影响消除研究
3.1 BP神经网络技术
BP神经网络算法,也称反向传播神经网络算法,是一种用于前向多层神经网络的反向传播学习算法.其基本思想是对组成前向多层网络的各人工神经元之间的连接权值进行不断的调整,进而逐步使误差函数沿梯度方向降到最小.最基本的BP神经网络包括输入层、隐性层和输出层3层前馈神经网络,其拓扑结构如图11所示.信息输入至神经网络后,首先由输入层节点传递至隐藏层节点,经过人工神经元作用之后,再传至下一层,如此层层传递下去,直至最终传至输出层并输出期望结果.

图11 BP神经网络模型结构
3.2 温度-频率的BP神经网络模型
下面基于监测数据建立模态频率和环境温度的BP神经网络模型.建模时采用3层级联前向神经网络,输入层为1个神经元,代表环境温度变化;输出层为4个神经元,代表结构前4阶模态频率;中间层经测试后确定为5个神经元.训练样本选取前144h的数据,测试样本为后24h的数据.鉴于数据采集时的温度变化范围,本文所建立的模型只适用于温度变化范围为18~60℃.
图12给出了面内1阶竖弯振型频率的训练样本和测试样本的拟合结果,并将其与实测频率数据进行对比分析.由图可知,训练样本拟合结果和测试样本拟合结果同实测数据变化趋势相同,且数值与实测值吻合较好.
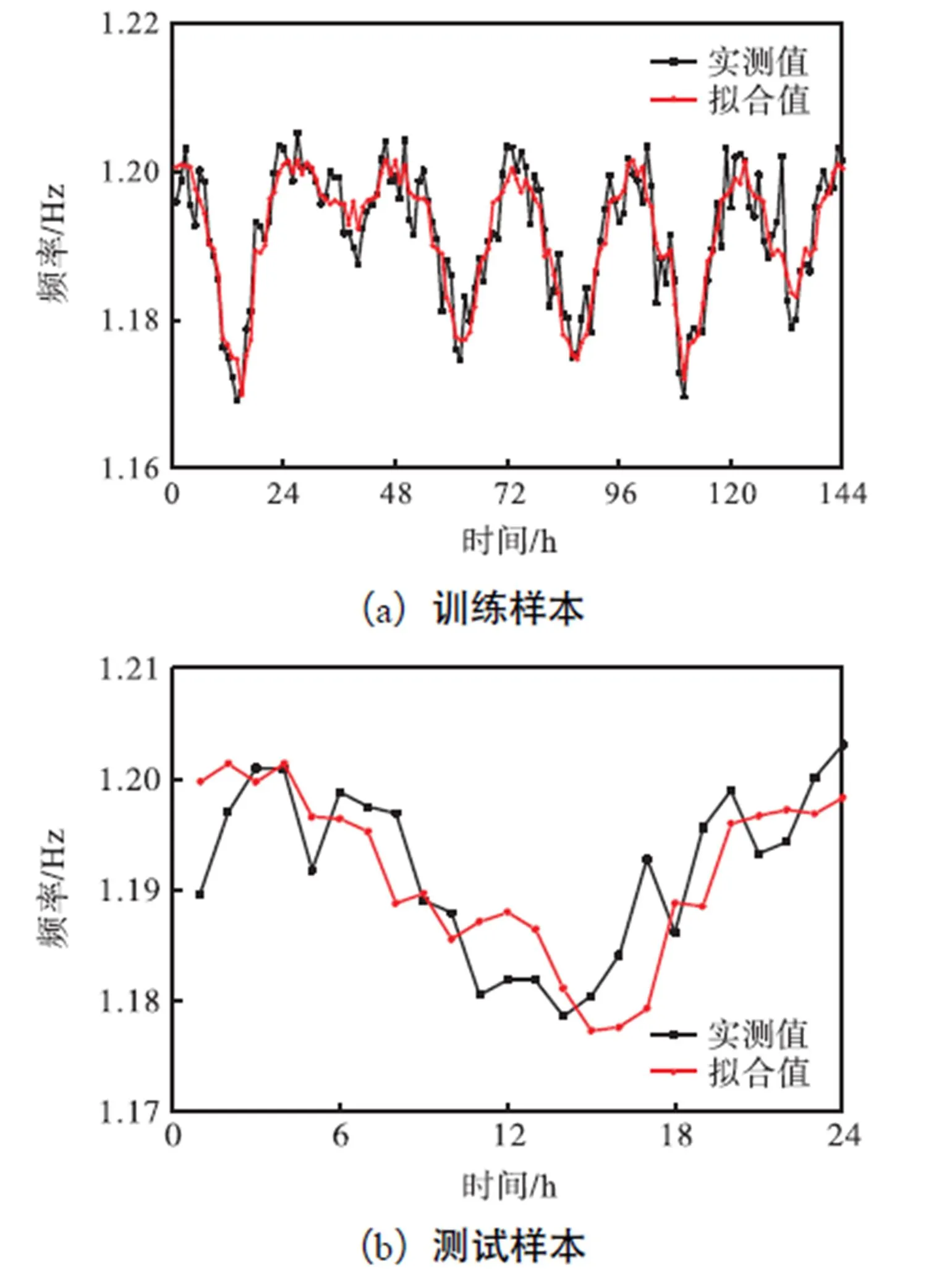
图12 面内1阶竖弯振型频率的BP神经网络模型拟合结果
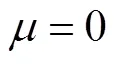
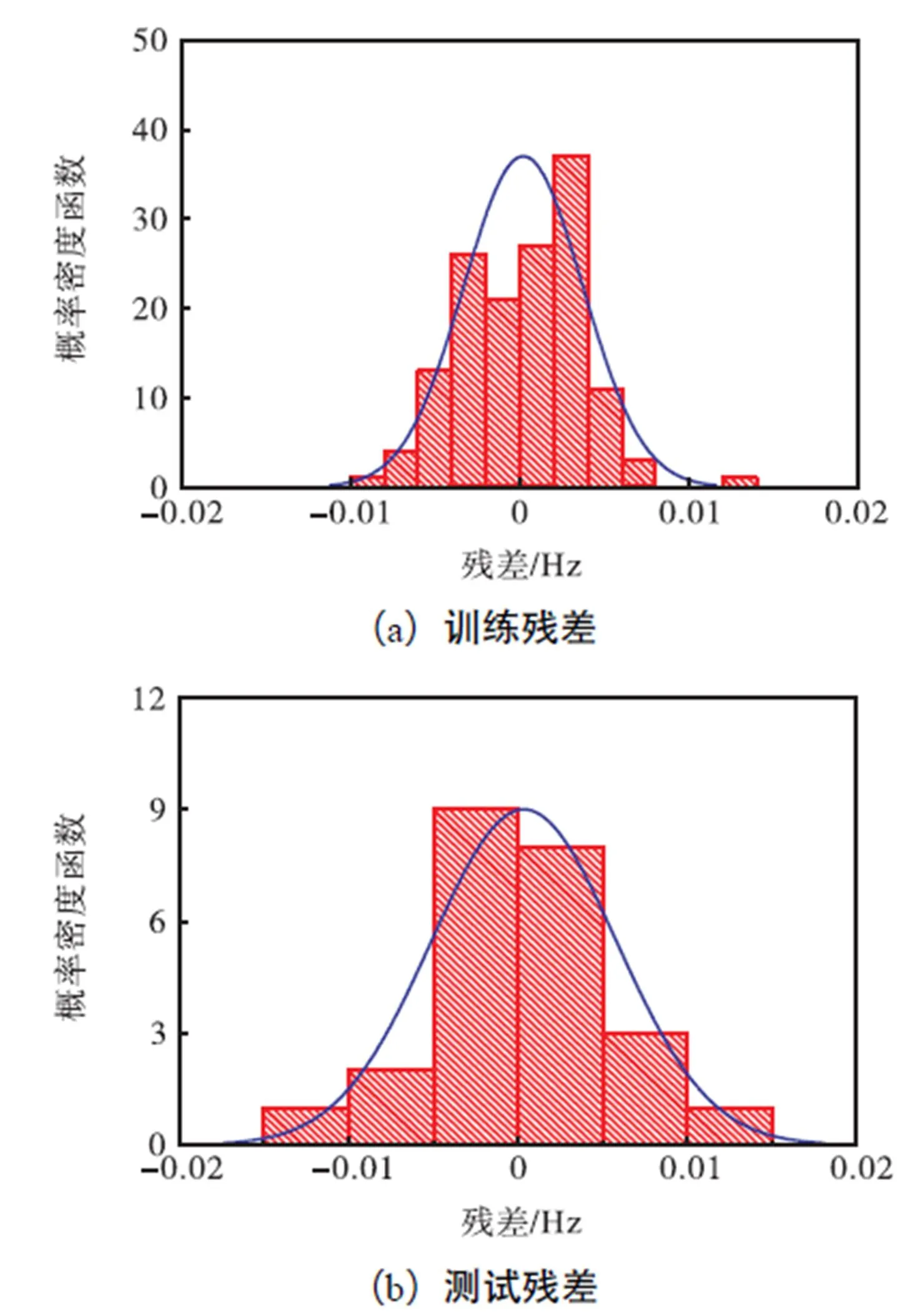
图13 面内1阶竖弯振型频率的BP神经网络模型残差分布
为进一步研究模型的泛化能力,表3记录了前4阶频率的模型误差评价参数.前4阶频率训练样本和测试样本的均方差和偏度均接近于零,峭度均接近于3,说明BP神经网络模型能比较充分地反映数据的非线性关系.因此,采用BP神经网络技术可为模态频率与环境温度建立合理的非线性映射模型.
3.3 温度影响的消除
建立温度-频率的BP神经网络模型后,可利用模型消除温度对频率的影响,计算公式[13]如下:
表3 BP神经网络模型误差参数
Tab.3 Error parameters of BP neural network model
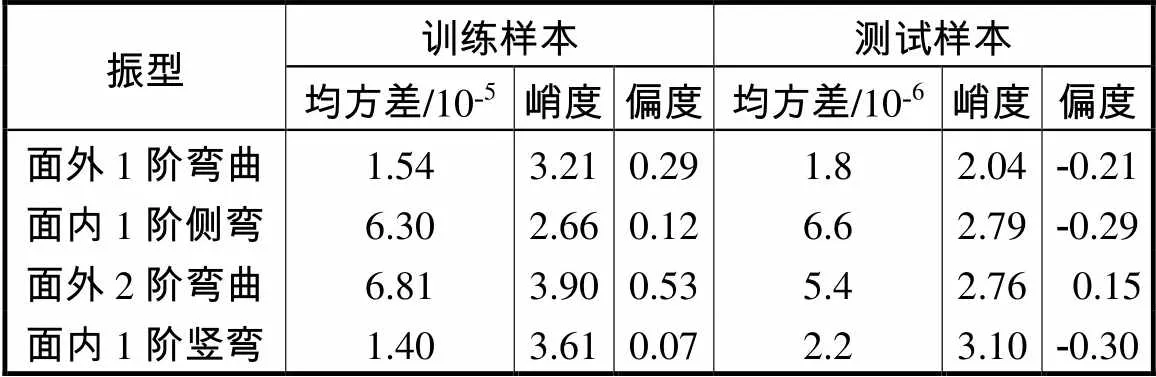
振型训练样本测试样本 均方差/10-5峭度偏度均方差/10-6峭度偏度 面外1阶弯曲1.543.210.291.82.04-0.21 面内1阶侧弯6.302.660.126.62.79-0.29 面外2阶弯曲6.813.900.535.42.7600.15 面内1阶竖弯1.403.610.072.23.10-0.30
图14为消除温度影响后的面内1阶竖弯频率的时程曲线与实测值的对比.从中可以看出,在消除温度影响后,结构模态频率以24h为周期的波动已大幅削弱,且结构模态频率方差由8.69×10-3下降到2.45×10-5.综合来看,BP神经网络模型可很好地反映模态频率与环境温度之间的关系.基于该模型消除温度影响后的模态频率,可以更好地表征结构自身的动力特性,进而应用于结构安全评估.
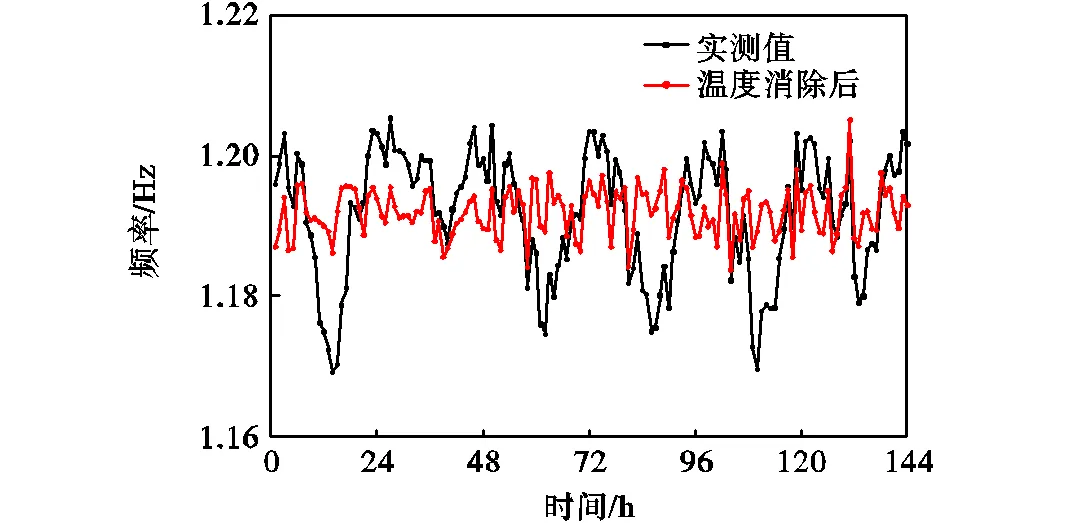
图14 消除温度影响后的面内1阶竖弯振型频率时程曲线
4 结 论
本文以潍坊市白浪河摩天轮钢结构为研究对象,通过数值模拟和实测数据分析对圆拱形钢结构模态频率的温度影响及消除进行研究,得到主要结论如下.
(1) 环境温度主要通过改变材料的弹性模量和结构状态来改变圆拱形钢结构的模态频率,且结构约束不同其模态频率的温度影响规律也不同,需要根据实际结构形式进行具体分析.
(2) 监测结果表明,白浪河摩天轮结构模态频率随温度升高而降低,在监测时间内频率最大变化幅度为3.04%;面内振型频率所受温度影响高于面外振型,其中结构状态改变是面内振型频率变化的主要 因素.
(3) 采用BP神经网络建立的模态频率-环境温度模型具有很好的拟合和预测效果,利用建立的模型可消除温度对频率的影响,为进一步的结构安全评估提供有效数据.
[1] 李爱群,丁幼亮,费庆国,等. 润扬大桥模态频率识别的环境变异性研究[J]. 东南大学学报:自然科学版,2007,37(2):245-250.
Li Aiqun,Ding Youliang,Fei Qingguo,et al. Environmental variability in modal frequency identification of Runyang Cable-Stayed Bridge[J]. Journal of Southeast University,2007,37(2):245-250(in Chinese).
[2] Ni Y Q,Zhou X T,Ko J M. Experimental investigation of seismic damage identification using PCA-compressed frequency response functions and neural networks[J]. Journal of Sound and Vibration,2006,290(1/2):242-263.
[3] Sohn H,Farrar C R,Hunter N F,et al. Structural health monitoring using dtatistical pattern recognition techniques[J]. Journal of Dynamic Systems Measurement and Control,ASME,2001,123:706-711.
[4] Zhang Deyi,Bao Yuequan,Li Hui,et al. Investigation of temperature effects on modal parameters of the China National Aquatics Center[J]. Advances in Structural Engineering,2012,15(7):1139-1153.
[5] Zhou Huafei,Ni Yiqing,Ko J M. Eliminating temperature effect in vibration-based structural damage detection[J]. Journal of Engineering Mechanics,2011,137(12):785-796.
[6] 王立新,朱嘉健,姜 慧. 珠江黄埔大桥模态频率连续监测中的温度影响II:温度影响及建模分析[J]. 震灾防御技术,2016,11(2):251-260.
Wang Lixin,Zhu Jiajian,Jiang Hui. Temperature influence in modal frequency continuous monitoring of Huangpu suspension bridge on the Zhujiang River[J]. Technology for Earthquake Disaster Prevention,2016,11(2):251-260(in Chinese).
[7] 滕 军,卢云军,朱焰煌. 大跨空间钢结构模态频率的温度影响监测与分析[J]. 工程抗震与加固改造,2010,32(3):36-41.
Teng Jun,Lu Yunjun,Zhu Yanhuang. Monitoring and analysis of temperature’s effect on frequency of large span spatial steel structure[J]. Earthquake Resistant Engineering and Retrofitting,2010,32(3):36-41(in Chinese).
[8] 康 婷,许 金,白 应,等. 轴向变形对拱自振频率影响的样条有限点法[J]. 地震工程与工程振动,2012,32(3):41-46.
Kang Ting,Xu Jin,Bai Ying,et al. Spline finite point method for analyzing effect of axial deformation on natural frequencies of arch[J]. Journal of Earthquake Engineering and Engineering Vibration,2012,32(3):41-46(in Chinese).
[9] 滕兆春,李万春. 变曲率平面拱的自由振动分析[J]. 兰州理工大学学报,2017,43(2):167-172.
Teng Zhaochun,Li Wanchun. Free vibration analysis of plane arches with variable curvature[J]. Journal of Lanzhou University of Technology,2017,43(2):167-172(in Chinese).
[10] 张高明,马 明,宋 涛. 潍坊摩天轮节点参数化设计及计算分析[J]. 建筑结构,2016,46(3):65-69.
Zhang Gaoming,Ma Ming,Song Tao. Parametric design and analysis of the joint in the structure of the Wei-fang Sky Wheel[J]. Building Structure,2016,46(3):65-69(in Chinese).
[11] Xia Y. Long term vibration monitoring of an RC slab temperature and humidity effect[J]. Engineering Structures,2006,28(3):441-452.
[12] 邓 扬. 基于长期监测数据的大跨桥梁结构状态预警与评估方法及其应用[D]. 南京:东南大学,2011.
Deng Yang. The Method and Application of State Warning and Evaluation of Large Span Bridge Structure Based on Long-Term Monitoring Data[D]. Nanjing:Southeast University,2011(in Chinese).
[13] 樊可清,倪一清,高赞明. 大跨度桥梁模态频率识别中的温度影响研究[J]. 中国公路学报,2006,19(2):68-73.
Fan Keqing,Ni Yiqing,Gao Zanming. Research on temperature influences in long-span bridge eigen frequencies identification[J]. China Journal of Highway and Transport,2006,19(2):68-73(in Chinese).
(责任编辑:樊素英)
Investigation of Environment Temperature Effects on Modal Frequency of Circular Arch Steel Structure
Liu Zhe1,Ding Yang1, 2,Zong Liang1, 2
(1. School of Civil Engineering,Tianjin University,Tianjin 300072,China;2. Key Laboratory of Coast Civil Structure Safety(Tianjin University),Ministry of Education,Tianjin 300072,China)
To investigate the time-varying characteristics of the modal frequency of circular arch steel structure under environmental temperature,the White-Wave River Ferris wheel in Weifang is taken as the research object in this study. The temperature influence of the modal frequency is studied by numerical simulation and statistical analysis of actual monitoring data. A regression model of modal frequency-temperature is also established based on the back propagation(BP)neural network technology for eliminating the temperature influence. The results show that temperature affects the modal frequency of structure by changing the mechanical properties and structural state of the structural material. For the White-Wave River Ferris wheel,the modal frequency decreases while the temperature increases,and the maximum change of frequency during the monitoring period is 3.04%. The temperature sensibility of the in-plane vibration mode frequency is higher than that of the out-plane vibration mode. The change of structural state is the main factor of the in-plane modal frequency vibration. The model established by BP neural network can accurately reflect the relationship between modal frequency and temperature. The frequency-temperature regression model can effectively eliminate the temperature influence of structure modal frequency.
environmental temperature;circular arch steel structure;modal frequency;BP neural network
10.11784/tdxbz201804075
TU311
A
0493-2137(2019)02-0183-08
2018-04-20;
2018-09-03.
刘哲(1986— ),男,博士研究生,liuzhe0624@126.com.
丁阳,dingyang@tju.edu.cn.
国家重点研发计划资助项目(2016YFC0701103);国家自然科学基金资助项目(91315301-06);天津市自然科学基金资助项目(13JCZDJC35200);天津大学滨海土木工程结构与安全教育部重点实验室开放课题基金资助项目.
the National Key Research and Development Program of China(No. 2016YFC0701103),the National Natural Science Foundation of China(No. 91315301-06),the Natural Science Foundation of Tianjin,China(No. 13JCZDJC35200),the Open Project Fund of the Key Laboratory of Coast Civil Structural Safety of Ministry of Education of Tianjin University.
