一种基于混沌粒子群改进的果蝇优化算法*
2019-01-14刘晓悦李朋园
刘晓悦,李朋园
(华北理工大学电气工程学院,河北 唐山 063000)
0 引言
果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)是一种新型的群智能全局优化算法,是近几年台湾学者潘文超于2012年以果蝇觅食行为为基础最新研究出的一种优化算法[1],与以往的群智能算法(如粒子群算法[2],蚁群算法[3]等)相比,果蝇算法寻优机制简单易懂,搜索过程仅包含嗅觉和视觉搜索,重要参数为种群规模和最大迭代次数,具有优良的全局优化能力[4]。因此,一经提出就引起了国内外学者的广泛关注,目前已成功应用于函数优化[5]、神经网络[6]、企业经营效绩评估[7]等。
然而,由于FOA的优化过程具有较强的随机性,其在搜寻最优解时引入了一些盲目搜索,会造成收敛过早和计算速度较慢等问题,尤其在求解高维复杂函数的过程中,FOA易陷入局部极值而造成较大的误差[8]。
本文提出一种最新研究的改进果蝇优化算法,通过引入一些改进策略来提高其全局寻优能力及收敛速度。改进策略如下:
1)引入混沌映射中的Logistic映射来生成果蝇群体的初始位置,进而提高其初始种群的多样性。
2)引入粒子群算法(PSO)的更新策略来降低FOA搜寻最优解时的盲目性。
1 基本果蝇优化算法
果蝇能够通过其在嗅觉和视觉上先天的优秀特性,利用感知器官搜集空气中的气味,进而找到距离较远的食物源。果蝇算法(FOA)即根据其觅食特性,模拟寻优过程,能够在更宽范围找出最优解。同时,它还具有逻辑易理解、需调整的参数少等特点[9]。图1显示了果蝇群落搜寻食物的迭代过程。

图1 果蝇群体觅食过程
根据果蝇觅食特性,FOA寻优过程分为以下几步:
Step1:位置初始化。

Step2:嗅觉搜索。

Step3:将Si代入到式(4)中求解得到个体所在坐标的气味浓度(Smelli):
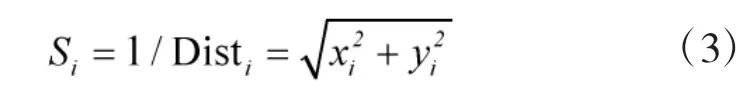

式中,Si为气味浓度判定值;Object function为判定函数。
Step4:在搜寻到群体中最佳的Smelli以及该个体的位置:

Step5:视觉搜索。

Step6:开始迭代优化,重复执行Step2~Step5。直到达到最大迭代次数为止。
通过分析等式(2)和式(3)可以发现,FOA有一些缺陷会限制其优化性能:
1)由于Si>0,FOA在定义域中存在负数时,FOA无法解决优化问题。
2)当x_axis和y_axis的值固定时,Si不遵循均匀分布。由于其不遵循均匀分布,潜在解不能再定义域中均匀产生;也就是说,Si不能在定义域中均匀搜索,因此,果蝇群失去了搜索全局最优解的能力,陷入局部最优,降低了收敛速度和收敛精度,即过早收敛的问题。
2 IFOA
为了解决FOA收敛速度慢以及收敛过早的问题,引入了上述算法来对其记性改进,具体步骤如下:
Step1:参数初始化。主要参数为最大迭代次数(Maxgen),群体规模(Sizepop),初始权重 η0和权重系数(β),控制参数,初始值 Hi。
Step2:混沌算法对初值具有很强的敏感性,而且有较大的随机性和遍历性。因此,正是利用混沌搜索的这些特性在生成果蝇群的初始位置时来提高其多样性[10]。而Logistic方程是一个典型的混沌映射系统[11]:

将式(7)引入进来得到初始位置x_axis,y_axis。

Step3:由果蝇个体与原点的距离计算气味浓度判定值(Si)。
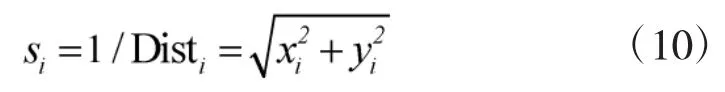
Step4:将Si代入式(11)中,计算出每个果蝇个体所在位置的气味浓度值(Smelli)。之后由式(12)得到浓度极值,并求出适应度函数值。

最后选择具有最佳适应度值的果蝇个体的位置为全局最优位置(gbestX,gbestY),选其最佳适应度为局部最优LbestX,LbestY。
Step5:通过PSO来更新搜索范围,由下式来更新 Vx,Vy。

式中,ω 为惯性权重,r1,r2是在[0,1]范围内的随机值。
将 Vx,Vy代入式(14)中进行更新后,再代入到式(10)~式(11)中进行迭代运算。
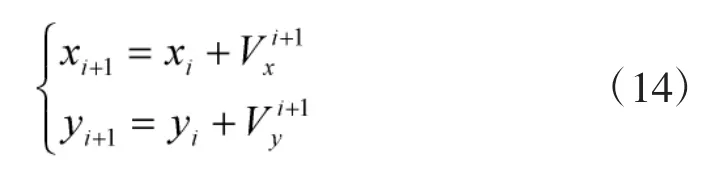

ω则根据线性递减权重(LDW)进行更新,设ω0=0.9,之后由LDW原则递减到0.3,其具体形式为:
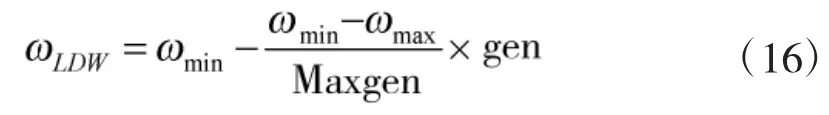
Step6:果蝇群体飞向Smelli极值对应个体的坐标(x,y)。

Step7:进行优化迭代,只有当适应度函数值不再优于上一步迭代的值或者gen达到最大时才停止。不然返回至Step5。
3 仿真验证及分析
3.1 测试函数验证
抽取了5个函数[13]为测试函数来对IFOA进行寻优验证。IFOA会对每个函数寻优100次,只有当求得的最优解在10-4以内才停止。由以下两个性能指标作为标准:平均有效迭代次数(Average Valid Iteration Number,AVIN)和成功率(Percentage of Success,PS)[14]。
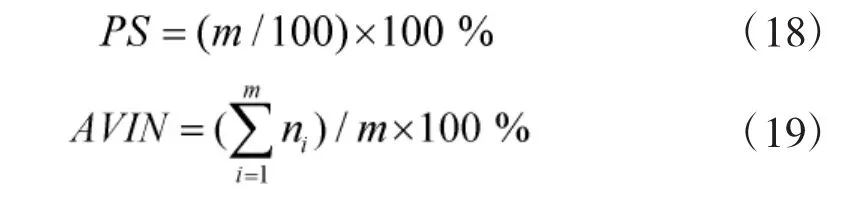
式中,m表示100次运行中最优值达到理想效果的次数,ni表示第i次成功的迭代次数。
参数设置:
PSO:Maxgen=300,sizepop=50,c1=c2=2,ωmax=1.3,ωmin=0.3,Vmax限制在 20%。
FOA:Maxgen=300,sizepop=50,LR=[-20,20],FR=[-20,20]。
GA:Maxgen=300,sizepop=50,具有交叉概率的单点交叉为0.7,具有突变概率的离散突变为0.1。
3.2 测试结果与分析
3.2.1 测试结果比较
每个函数重复100次,测试结果如下页表2所示。从表2可以看出,在求解GP,SH,BR,RA,SP时,IFOA的平均值更接近于理论最优值,IFOA的标准差明显小于FOA标准差。因此,得出结论,IFOA比FOA求解最优值性能更好。
从图2可以看出,IFOA目标值的变化曲线比FOA的目标值下降得快得多,并且IFOA的搜索性能优于FOA。所以也可以得出结论,IFOA比FOA搜寻速度更快,精度更高。

图2 4种算法在函数上的收敛曲线

表1 基准函数

表2 IFOA、FOA、PSO和GA的均值与标准差

表3 IFOA与FOA的鲁棒性分析

表4 IFOA与PSO、GA的鲁棒性分析
3.2.2 鲁棒性分析
表3显示了求解最优解100次后FOA和IFOA的PS和AVIN。从表3可以看出,IFOA能够为每个函数找到最优解,并且PS更高。此外,IFOA的AVIN比明显FOA要小。因此,得出结论,IFOA比FOA更有效可靠。
3.3 IFOA与其他算法的比较
由表2可知,在为所有函数求解时,IFOA的均值和标准差优于GA。且对于BR,RA和SP的求解,其均值和标准差优于PSO。可得知,IFOA比PSO和GA更有效。图2(a)~图2(e)的曲线也正验证了这一结论。
由图2(b)和图2(c)可知,IFOA 收敛性大大提高。总体而言,IFOA的表现优于PSO和GA。由表4可知,在搜寻全局最优解时,IFOA比GA和PSO具有更高的PS。综上所述,IFOA的鲁棒性更好。
4 结论
果蝇算法是一种新型启发式群智能算法,但FOA算法与群智能算法一样,普遍存在早熟、收敛精度低、收敛速度慢等不足。为此,为了提高果蝇初始种群的多样性,采用混沌搜索去初始化果蝇位置,同时引入粒子群算法去优化果蝇算法的全局寻优能力进行二次寻优,通过函数验证,并与其他传统算法进行比较分析,仿真结果表明本文提出的IFOA算法鲁棒性较强,收敛速度更快且精度更高。但是该算法有些问题还需要进一步研究和改善,在下一步研究工作中考虑引入模拟退火等算法来提高FOA的局部寻优能力。
