基于光纤光栅的复合材料结构损伤识别方法*
2019-01-14崔建国张善好于明月蒋丽英林泽力
崔建国,张善好,于明月,蒋丽英,林泽力
(1.沈阳航空航天大学自动化学院,沈阳 110136;2.沈阳航空航天大学电子信息工程学院,沈阳 110136;3.故障诊断与健康管理技术航空科技重点实验室,上海 201601)
0 引言
复合材料由于其重量轻、特性优异等特点在现代飞机上得到广泛应用。但由于飞机飞行时受多种因素的影响,可能会引起飞机复合材料结构出现损伤,甚至导致飞行事故的发生。因此,及时识别出复合材料结构损伤已成为目前业界关注的关键问题之一。
为解决复合材料结构损伤识别关键技术,国内外诸多学者进行了较深入研究。李伟等人采用小波神经网络对复合材料结构不同损伤模式的识别进行了研究[1]。由于小波神经网络自身结构特点,使得小波神经网络模型极易出现陷入局部极小或不收敛等问题[2]。赵进昌等人采用SOM神经网络对复合材料损伤监测[3],但SOM训练识别模型的时间较长,给实际应用带来诸多不便。王明采用BP和经验模态分解相结合的方法,实现了复合材料板材的损伤识别和定位[4]。但由于经验模态分解的模态混叠现象,改变了本征模函数的物理意义,结果影响了识别准确率。本文提出采用集合经验模式分解(Ensemble Empirical Mode Decomposition,EEMD)方法对原始信号进行处理,提取特征信息,从而可以避免经验模态分解时出现的模态混叠现象[5],与此同时,结合K-ELM神经网络无局部极小问题、学习收敛速度快、训练时间短的特点[6],采用光纤光栅监测技术对飞机复合材料结构损伤识别方法进行了研究。
1 理论基础
1.1 EEMD分解
EEMD分解是针对经验模式分解(Empirical Mode Decomposition,EMD)的不足进行改进而形成的新方法。EEMD可以精确地应用于非线性、非平稳的信号处理过程中。在原始信号被EMD分解前,利用高斯白噪声均匀分布的统计特性,将高斯白噪声加入原信号中,使信号在不同尺度上具有连续性,以促进抗混分解,从而可以避免模态混叠,使分解更具有完备性,可获得更好的分解效果[7]。
EEMD 分解步骤[8-9]如下:
1)若原始信号为x(t),在原始信号中分多次加入长度相同的高斯白噪声ni(t)(所加入的高斯白噪声分布特性均为正态分布),则每次加入白噪声后的信号变为:
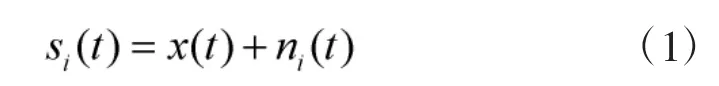
其中,i代表加入白噪声的次数。
2)对被加入噪声后的新信号si(t)分别进行EMD分解,获得IMF分量imfij和余项ri;imfij为在第i次被加入白噪声后的信号经过EMD分解获得的第j个IMF分量。
3)若随机序列不相关,则其统计均值为零,将imfij进行平均,EEMD分解结果为

其中,M为加入白噪声的个数。
1.2 奇异熵特征的提取
由于奇异熵可在整体上定量衡量原始信号的复杂性或不确定性程度,以表征复合材料结构的不同损伤[10]。现以EEMD分解的IMF分量为基础,将奇异熵作为复合材料结构损伤的特征信息进行提取。提取过程如下:
1.2.1 构建特征向量矩阵
采用EEMD对原始信号进行自适应分解,得到频率由高到低排列的各阶IMF分量和残余分量。提取各阶IMF分量作为初始特征向量矩阵,其中m为IMF分量个数。
1.2.2 奇异值的获取
由矩阵分析理论知,必然存在矩阵U、矩阵V和对角线矩阵Λ,则初始特征向量矩阵可表示为:

1.2.3 对奇异值进行归一化处理

1.2.4 计算奇异熵
EEMD的奇异熵定义为:
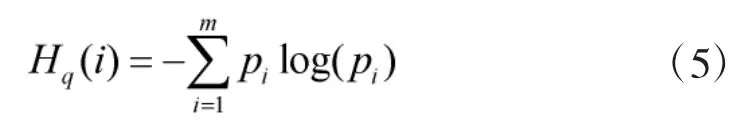
1.3 核函数极限学习机
为提高数据的线性可分性,将核函数引入到极限学习机中,构造核函数极限学习机(Kernel Ex treme Learning Machine,K-ELM)。单隐层极限学习机的模型结构如下页图1所示,由输入层、隐含层和输出层组成。为模型输入,为模型输出,为隐含层神经元,ωLn是输入层神经元与隐含层神经元间的权重,βnK是隐含层神经元与输出层神经元间的权重。
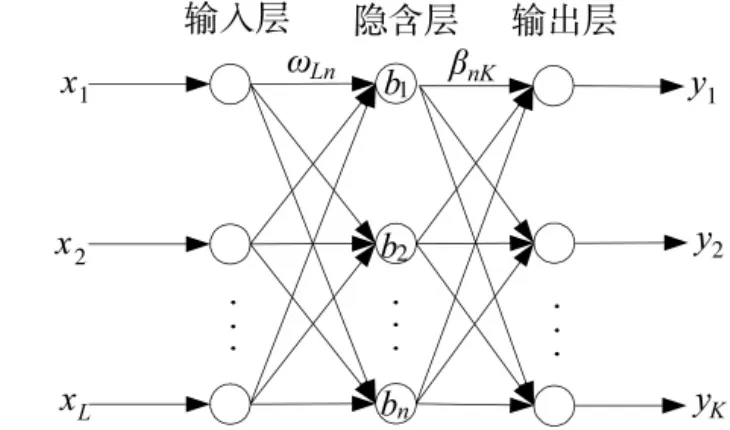
图1 单隐层极限学习机的模型结构
为简明ELM神经网络模型,将ELM神经网络模型抽象为

式中,h(x)为隐含层神经元的传递函数,β为网络输出权重。ELM算法通过最小化输出权重β保证神经网络的泛化能力。通常β取其最小二乘解,计算方法为
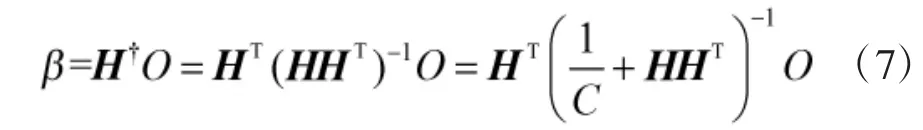
通过引入核函数可以将输入空间样本数据映射到高维空间,通过內积运算处理样本数据。本文将高斯核函数应用到极限学习机中[11]。对于K-ELM神经网络,其模型可以抽象为
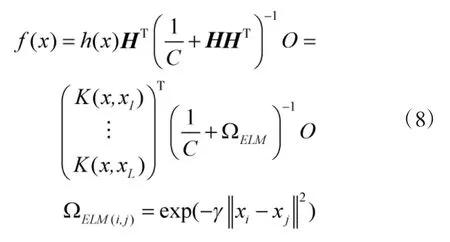
式中,ΩELM为所选的高斯核函数,L为输入层维数。
2 飞机复合材料结构损伤识别方案
飞机复合材料结构损伤识别方案如图2所示。

图2 飞机复合材料结构损伤识别方案
首先,对复合材料结构件进行冲击,而后对其进行疲劳拉伸试验,通过优化布局在复合材料层合板上的光纤光栅传感器对试验件所产生的应变数据进行募集,得到结构损伤信息。其次,采用EEMD方法对得到的结构损伤信息进行自适应分解,并提取奇异熵特征向量。最后构建奇异熵特征向量矩阵作为建模数据,分别建立基于K-ELM和BP神经网络的结构损伤识别模型,并通过测试数据对两种模型的识别有效性进行验证。
3 试验数据的获取与特征提取
3.1 获取试验数据
采用型号为BA9912-G0827尺寸为100 mm2×150 mm2的复合材料层合板作为试验件,多层对称层合板的一半铺层形式为[45/-45/0/-45/0/45/0/90/0/45/-45/0]s,单层铺层厚度为0.18 mm,整个层合板共24层。将光纤光栅传感器共4个均匀分布在试验件的表面。准备工作完成后,先对试验件进行冲击,而后采用疲劳拉伸实验机对试验件进行疲劳拉伸试验,直至试验件破坏。破坏的试验件如图3所示。

图3 破坏的试验件
复合材料疲劳损伤形式主要表现为:分层、界面脱胶、基体裂纹、纤维断裂等等[12]。当负载较小时,损伤主要表现为分层形式[13],采用复合材料超声检测仪(图4)对试验件进行无损检测,通过反射波与界波之间出现的新波峰波谷位置,可判断出分层损伤的损伤程度。经过分析,可将试验件分层损伤的损伤程度分为完好、初始损伤、损伤扩展和损伤失效,具体分析如下。

图4 FCC-B-1复合材料超声检测仪
首先对试验件进行重锤冲击,并对其损伤进行检测,发现了深度为三层直径为5 mm的圆坑。此时,试验件处于初始损伤阶段。在此基础上,对其进行疲劳加载实验,随着疲劳加载次数的增加,试验件不断呈现新的损伤。当试验件的11层到13层呈现2 mm×6 mm的条状分层损伤时,处于损伤扩展阶段。当试验件的6层到8层处呈现直径为6.5 mm的圆形分层损伤时,试验件处于损伤失效阶段。由单个传感器采集到的完好、初始损伤、损伤扩展和损伤失效原始应变数据如图5所示。本文将对其损伤识别进行研究。
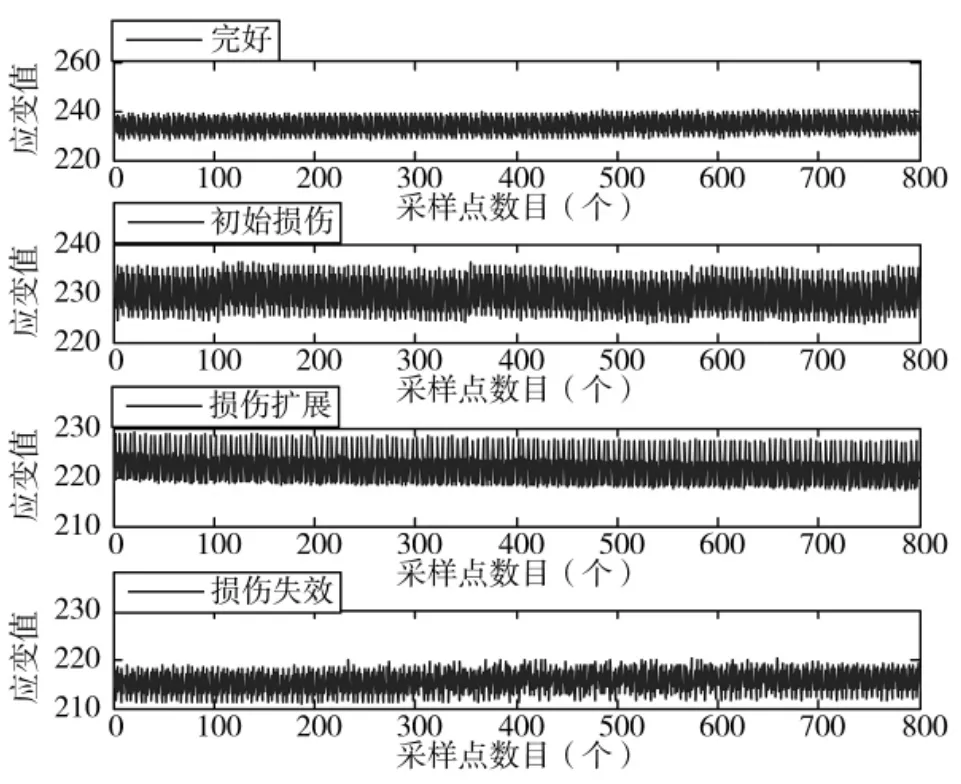
图5 不同损伤模式的原始应变
3.2 特征提取
首先,对传感器感知的分层损伤原始信息进行预处理,滤掉干扰波动数据,然后对预处理后的数据进行EEMD分解,得到各阶IMF分量,最后采用1.2节方法提取奇异熵特征,过程如下。
将试验采集的8 000个原始应变值以每10个应变值进行1次EEMD分解,计算每次分解得到的各阶IMF分量的奇异熵,结果如表1所示。
表1中第1~200组数据为完好状态计算得到的奇异熵,第201~400组数据为初始损伤状态计算得到的奇异熵,第401~600组数据为损伤扩展状态计算得到的奇异熵,第601~800组数据为损伤失效状态计算得到的奇异熵。采用第1~175组、201~375组、401~575组和601~775组奇异熵构建四维特征矩阵,作为模型构建数据。采用第176~200组、376~400组、576~600组和776~800组奇异熵构建4维特征矩阵,作为模型测试数据。
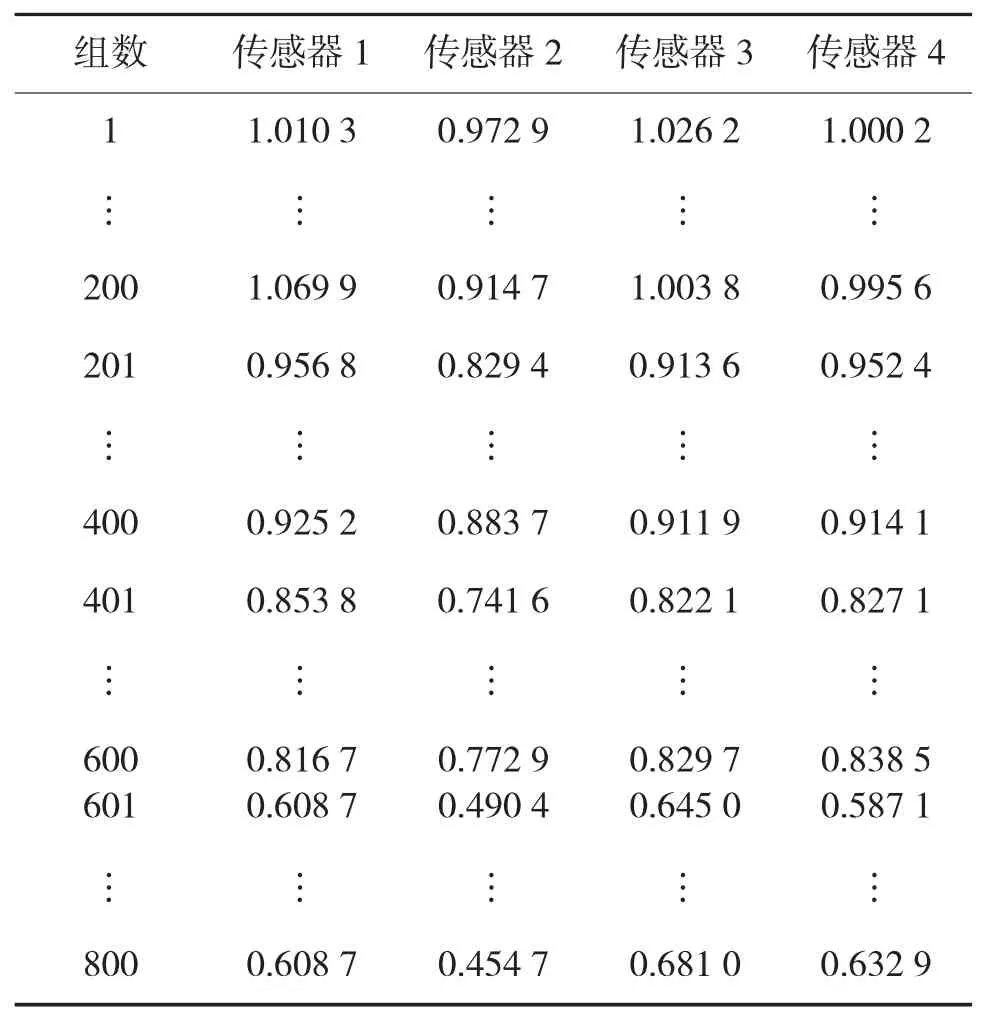
表1 不同传感器监测信息的奇异熵
4 损伤识别模型的构建与试验验证
4.1 损伤识别模型的构建
依据1.3节内容,本文设计了3层(即输入层、隐含层和输出层)K-ELM神经网络作为飞机复合材料结构损伤识别模型。结构损伤模式与识别模型的输出形式见表2。

表2 结构损伤模式与对应的输出形式
采用3.2节得到的建模数据作为识别模型的输入,创建复合材料结构损伤识别模型。所创建的损伤识别模型输入层的节点有4个,输出层的节点有1个。
4.2 识别效果验证
为验证所构建的K-ELM损伤识别模型的准确性,本文尚设计了BP损伤识别模型。采用3.2节测试数据分别对K-ELM和BP两个损伤识别模型进行试验验证,结果见下页表3和图6。
由表3可知,对感知的飞机复合材料结构损伤信息经过EEMD分解并提取奇异熵特征,采用K-ELM模型损伤识别的准确率为95%,明显高于BP神经网络损伤识别的准确率90%。上述两种识别模型的验证结果有一定的差异,很大程度归咎于BP算法容易陷入局部极小的固有特性和依靠经验试凑网络隐层节点数目的缺点,难以得到最优识别效果。而K-ELM识别模型在很大程度上克服了BP算法的缺点,具有良好的泛化识别能力,其网络不存在局部极小问题,而且其隐层节点数目依据训练样本数据在训练过程中自动确定,容易得到最优的识别效果。本次试验结果表明,K-ELM损伤识别模型对飞机复合材料结构有着较强的损伤识别能力。
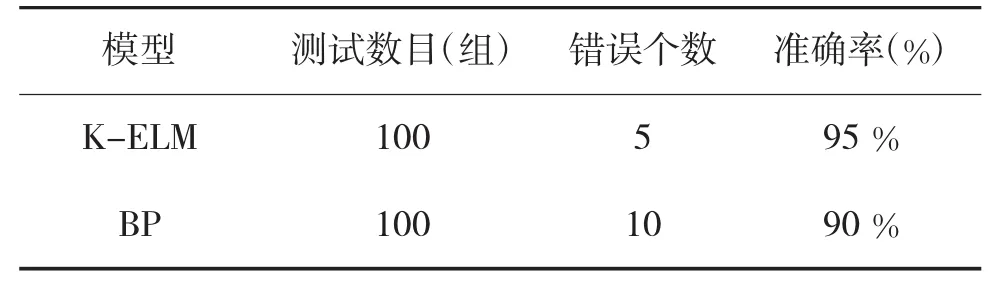
表3 K-ELM和BP两种损伤识别模型的测试结果
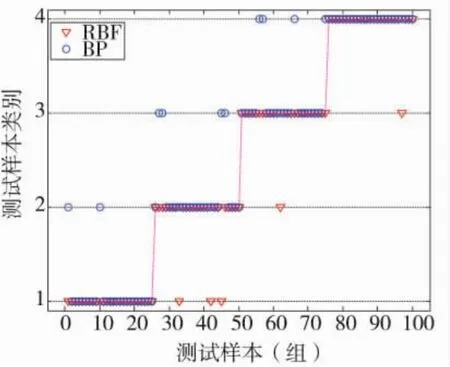
图6 K-ELM和BP两种损伤识别模型测试结果图
5 结论
以飞机复合材料层合板为研究对象,对其进行冲击和疲劳拉伸试验,通过优化布局在复合材料层合板上的光纤光栅传感器募集试验件所产生的应变数据;采用由经验模式分解改良而来的集合经验模式分解对试验件的原始应变信息进行分解,利用集合经验模式分解避免模态混叠的优点,保证分解后的每个IMF分量都具有完备物理意义,在最大程度上提高后续特征提取的准确性;引入奇异熵作为表征飞机复合材料结构损伤信息的特征量,清晰反应结构损伤信息中奇异成分的能量分布复杂程度,准确表征飞机复合材料结构损伤信息,保证了识别模型的有效训练,进而提高识别模型的识别能力;分别设计了K-ELM和BP两种结构损伤识别模型,通过试验数据对所设计两种模型的准确性进行了验证,结果表明K-ELM模型的损伤识别效果更好。
本文提到的损伤识别模型的识别准确率是在有限试验数据样本下得到的,实际应用过程中,仍需利用大量的试验数据去加以验证与完善。
综上所述,本文研究提出的基于EEMD和K-ELM的复合材料结构损伤识别方法,为飞机复合材料结构损伤识别提供了一条新思路,具有较好的应用前景。
