基于混合型扩散的无人机航拍图像去噪模型*

王 俊，杨成龙

（1.陆军军官学院基础部，合肥 230031；2.陆军军官学院研究生管理大队，合肥 230031）

0 引言

军用无人机作为现代空中军事力量的一员，具有隐蔽性好、无人员伤亡、效费比高等特点，在现代战争中的地位和作用日渐突出。在战场上，作战人员可以通过无人机完成情报侦察、军事打击、通信中继、空中预警等军事任务。其中，情报侦察是最基本的应用：无人机通过安装雷达、相机等设备，可以在战场上空进行高速信息扫描、低速飞行或者悬停凝视，为部队提供实时情报支持。但是受太阳辐射和大气等因素的影响，无人机上的航空摄影机所拍摄得到的目标图像在形成、传输和存储过程中难免会被噪声污染[1]，导致传回地面的目标图像质量不高，无法为作战提供准确的情报资源，因此，对无人机航拍图像的去噪研究显得格外重要。

近年来，基于偏微分方程的图像去噪方法因其良好的去噪效果而受到国内外学者的广泛关注，如P-M模型、全变分模型和四阶偏微分方程模型等。但这些去噪模型的处理对象基本上都是灰度图像，且通常是人为加入噪声进行研究，因此，噪声的方差等参数都已知[2]。而当前无人机航拍图像则不同，首先，它们大多为彩色图像，相比灰度含噪图像而言处理起来更为复杂；其次，我们并不知道噪声方差的大小。

为此，本文提出一种混合型扩散偏微分方程图像去噪模型，并从主、客观两方面对模型的去噪能力进行了评价，数值结果表明本文模型的图像去噪效果明显优于以往的方法。

1 改进的噪声方差估计法

对于噪声方差估计这一问题，最具代表性的方法是1994年Donoho和Johnstone提出的利用含噪图像的小波变换系数去估计噪声方差的方法，该方法可表示为：

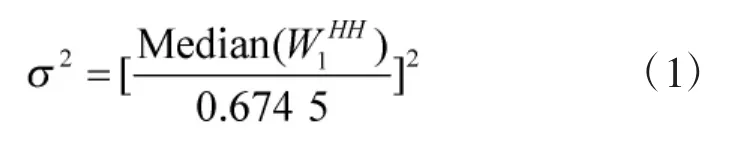
为证明本文提出的噪声方差估计法比Donoho的方法准确度高，下面以含噪图像Lena为例，用bior3.7小波对其进行1层小波分解。图1（a）是对Lena图像加入方差为10的高斯噪声得到的图像；图1（b）是用Canny边缘检测算子对低频图像LL进行边缘检测得到的图像；图1（c）是含噪图像经小波分解后得到的对角高频HH图像；图1（d）是对角高频HH图像去除边缘区域后所得的图像。可以看出，图1（d）主要是噪音信息，图像的细节信息几乎没有，因此，由其估计出来的噪声方差要更准确。下面再通过客观评价来证明：分别用Donoho方法和本文方法对加有不同噪声方差的Lena图像估计15次，取平均值作为噪声方差的估计值[5]，对应的实验数据如表1所示。

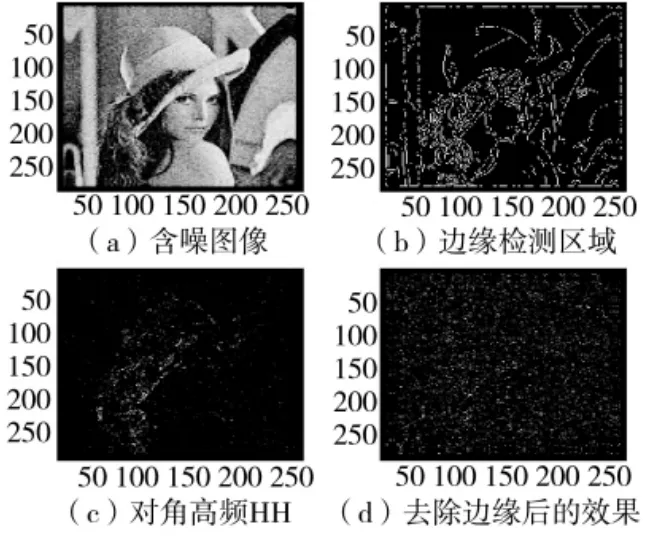
图1 去除边缘区域后的噪音信息

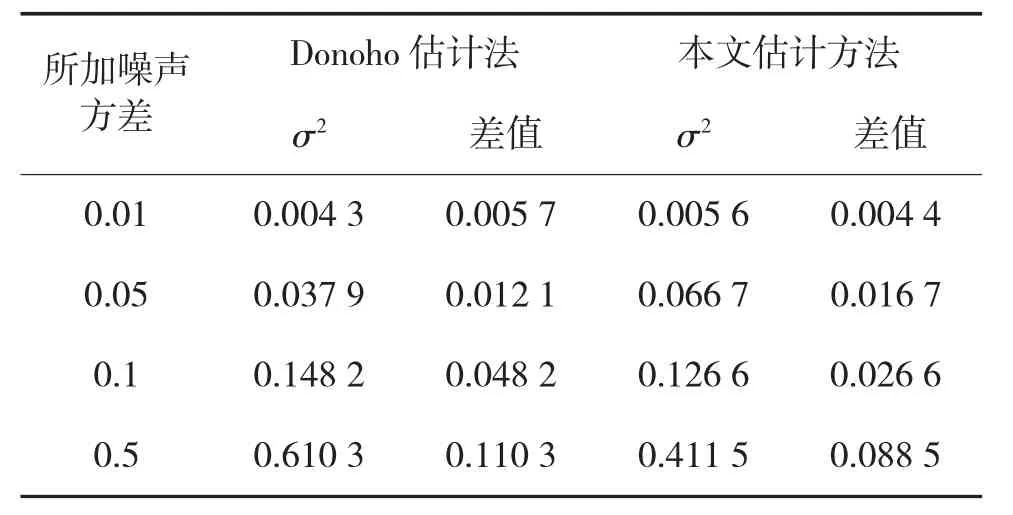
表1 噪声方差估计对照表

从表1噪声方差估计的差值大小可以看出，本文方法对噪声方差估计的准确性明显更高。

2 混合型扩散模型的提出

2.1 模型的建立

全变分模型和四阶偏微分方程模型是偏微分方程在图像去噪领域非常有名的两个模型，它们在图像去噪方面都有各自的特点，但也有不足之处，比如全变分模型处理图像平坦区域时会产生“块状效应”，使得图像出现局部细节特征丢失的现象；四阶偏微分方程模型容易造成图像光滑区域不平整的现象[6]。为此，本文将二者进行有效结合，并对模型中的扩散系数进行改进，得到一个混合型扩散去噪模型。

设u0为原始图像，u为观测到的图像，Ω为R2中的有界开子集，首先，本文将图像的能量函数取为：

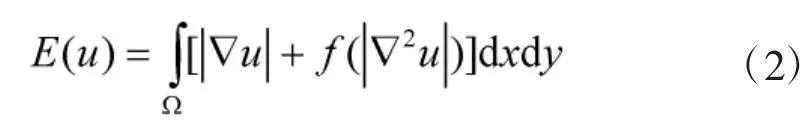
然后通过最小化全变分和梯度下降法得到如下去噪模型：

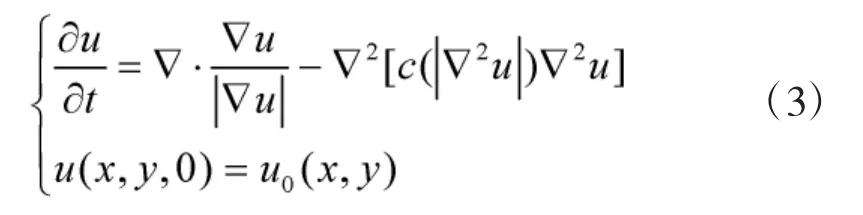
为避免当噪声梯度和图像信息梯度大小相近时图像细节信息被当作噪声去除掉的问题，本文提出将方差和梯度相结合的方法来共同度量图像局部特征[7]。因为在图像边缘处，图像纹理细节的方差远大于背景噪声的方差，于是将式（3）中的扩散系数表示如下：

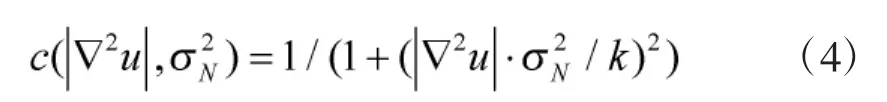
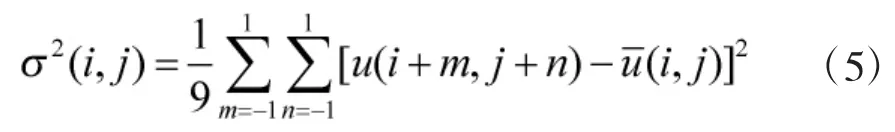
图2为改进的扩散函数的三维图，从图中可以看出，本文所选取的扩散系数c（·）可以很好解决去噪时误将图像的边缘信息当作噪声去除掉的问题[8-9]：在图像边缘或纹理复杂区域，所对应的和灰度方差都比较大，此时扩散系数函数c（·）较小，扩散被抑制，图像的纹理信息得以保护；相反，在图像的平坦区域，所对应的和灰度方差都比较小，此时扩散系数函数c（·）较大，扩散强烈，从而有助于消除噪声。

图2 扩散函数的三维图

综上所述，本文提出的混合型扩散模型的表达式如下：

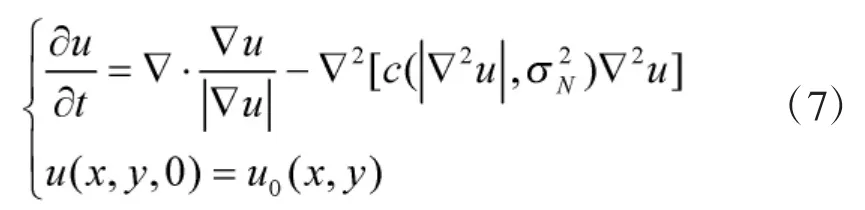
2.2 模型的去噪流程

图像噪声方差估计出来后，就可以利用本文提出的混合型扩散模型进行去噪处理，处理流程如图3所示。

图3 混合型扩散模型的去噪流程

3 实例分析

为验证本文方法的有效性，下面以一幅无人机航拍图像Loufang为实例，并以峰值信噪比PSNR、均方根误差MSE和相对误差RelErr为评价指标，将本文模型与全变分模型、四阶偏微分方程模型进行比较实验。其中，图4为各模型对Loufang图像的去噪效果对比，下页表2为经各模型处理后Loufang图像的各性能参数。

图4 各模型对Loufang图像的去噪效果

表2 去噪后Loufang图像的各性能参数

从图4可以看出，本文提出的混合型扩散模型对无人机航拍图像具有较强的去噪能力，且比全变分模型和四阶偏微分方程模型的去噪效果要好，在滤除噪声的同时还很好地保持了图像的边缘，使得去噪后的图像纹理细节更加清晰[10]。从表2的数据可以看出，一方面，和原无人机航拍图像相比，经本文模型去噪后的图像对应的PSNR都更大，MSE和RelErr都更小，说明本文模型达到了一定的去噪效果；另一方面，本文模型对应的PSNR最大、MSE和RelErr最小，说明其去噪效果最好。

4 结论

本文从无人机航拍图像的几个重要特征出发，首先提出了一种改进的噪声方差估计方法，该方法能够在不知道噪声参数的情况下较准确地估计出无人机航拍图像的噪声方差。其次，本文在全变分模型和四阶偏微分方程模型的基础上，通过对扩散系数的改进提出一种混合型扩散去噪模型，该模型较好克服了两去噪模型各自的缺点，既能较好地滤除噪声，又能使图像的细节特征得到保持，并且从各项实验数据看，本文模型在无人机航拍图像去噪方面有着一定的优势，所以本文模型是一个较好的图像去噪模型。