GaN太赫兹肖特基变容二极管倍频效率的研究

(南京电子器件研究所微波毫米波单片集成和模块电路重点实验室，江苏南京 210016)

太赫兹波具有穿透性强、使用安全性高、定向性好等技术特性，因此受到了世界各国的高度关注。由于太赫兹频段频率极高，导致可使用的太赫兹源的制造极其困难，太赫兹源成了制约太赫兹技术发展的瓶颈。目前用来制造太赫兹源的方法之一是利用肖特基二极管(SBD)进行倍频，利用SBD的C-V曲线的非线性使较低频率的信号通过非线性作用产生更高的频率分量。采用SBD的一个优点是由于SBD为多子器件，不存在扩散电容，使得其截止频率较高。

平面太赫兹肖特基倍频二极管普遍使用GaAs来制作，因为相较于目前常用的半导体材料GaAs具有最高的电子迁移率(8500 cm2/(V·s))，这使得GaAs器件具有很高的截止频率。采用GaAs制作的平面SBD截止频率理论上能达到10 THz量级，Teratech公司的AP1/G1/0P95能做到11～13 THz[1]。但是由于CaAs禁带宽度(1.42 eV)较窄，因而器件的反向击穿较低，这就限制了GaAs倍频二极管的功率输出，从而带来负载能力不足的问题。为了提高倍频二极管的输出功率，近几年来不少科研人员和研究机构将目光投向禁带宽度更大的GaN材料上，以寻求新的突破。GaN禁带宽度(3.45 eV)几乎是GaAs的三倍，从而显著地提高了器件的击穿电压和功率负载能力。但是GaN的电子迁移率几乎只是GaAs的1/8，这大大增加了器件的串联电阻。另一方面，由于目前GaN材料大多采用异质外延，导致GaN和衬底材料之间存在晶格失配和热应力失配等一系列问题，使得材料的缺陷密度较大。缺陷密度大不但会进一步降低电子迁移率，还会影响肖特基接触的性能降低击穿电压[3]。

尽管GaN材料由于生长工艺和自身特性导致其电子迁移率较低，但是其负载功率大的优势仍然有着诱人的应用前景。为了改善GaN太赫兹肖特基变容二极管的倍频特性，除了从器件的阳极尺寸、外延层掺杂浓度、外延层厚度等方面入手对器件进行优化设计外，还可以通过采用均相外延技术提高材料的质量，有效降低串联电阻并提高截止频率[4]。另一方面可以采用渐变掺杂的掺杂方式提高GaN太赫兹肖特基变容二极管的电容比，进而提高倍频效率[5]。渐变掺杂方式对材料的生长技术要求极高，目前还没有GaN渐变掺杂相关的文献报道，其实用性并没有得到证实。本文通过使用目前业内比较认可的Sentaurus TCAD对恒定掺杂和渐变掺杂进行仿真对比，验证了在一定的掺杂浓度下渐变掺杂能够提高GaN太赫兹肖特基变容二极管的倍频效率。

1 影响GaN肖特基二极管性能的相关因素

GaN太赫兹肖特基变容二极管的截面示意图和等效电路图如图1所示:

图1 GaN太赫兹肖特基变容二极管截面示意图Fig.1 Cross diagram of GaN terahertz Schottky varactor diodes

图1中，1为肖特基接触金属;2为加反偏电压时的耗尽层;3为未耗尽的n-掺杂层;4为n+掺杂层;5为欧姆接触金属。C为随耗尽层宽度变化而变化的电容;Repi为随耗尽层宽度变化而变化的外延层电阻;L为空气桥及相关串联的寄生电感，在没有外接连线时可以忽略不计;扩散电阻Rspread和缓冲层电阻Rbuffer为n+层的串联电阻，在高掺杂时n+层的串联电阻远比Repi小;Rcontact为欧姆接触电阻，在阴极面积为几十μm2量级以上时其值相对总电阻值很小，可以忽略不计。

1.1 二极管的串联电阻

如图2所示，二极管的串联电阻主要来自以下几个方面。总电阻:

式中:Vb为反偏电压;f为工作频率。

(a)外延层电阻Repi

外延层电阻Repi主要和耗尽区宽度以及外延层掺杂浓度有关:

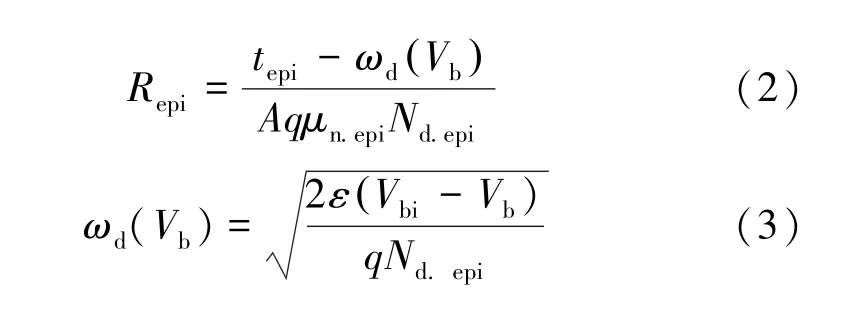
式中:Nd.epi为外延层掺杂浓度;μn.epi为外延层电子率;Vbi为内建电势差;Vb为反偏电压;ωd(Vb)为电压为Vb时外延层耗尽区宽度。GaN电子迁移率在一定掺杂范围内可大致求出。

式中:N为总掺杂浓度;T为绝对温度;Nref为1×1017cm-3;其他为拟合参数，具体如表1:只适用于掺杂浓度为1×1016～1×1018cm-3[3]。

表1 GaN电子迁移率公式参数Tab.1 Parameters of electron mobility for the formula

在阳极直径为1 μm时根据公式(4)计算得出外延层迁移率μn.epi;根据公式(2)和(3)计算出外延层电阻。由此得出不同外延层厚度对应最大电阻和掺杂浓度的关系如图2所示。

图2 外延层电阻与掺杂浓度的关系Fig.2 Relationship between resistance and doping concentration of the epitaxial layer

(b)n+层电阻Rspread和Rbuffer

扩散电阻Rspread主要与n+层掺杂浓度有关:

式中:δbuffer为趋肤深度;μbuffer为n+层电子迁移率。μbuffer主要受电离杂质散射和晶格振动散射影响，掺杂浓度越高，电场越大，温度越高都会降低电子迁移率从而增大电阻[1]，因此n+层的掺杂浓度应该适宜。根据式(7)，当频率f=300 GHz、掺杂浓度为2×1018cm-3时，δbuffer约为10 μm， 大于本文仿真设计的n+高掺杂层厚度，因此实际计算时使用n+层厚度Tn+代替δbuffer。当掺杂浓度为1018cm-3量级时，扩散电阻Rspreading相较于外延层电阻较小。

缓冲层电阻Rbuffer由式(8)得出。

式中，roc为肖特基阳极外延到阴极欧姆接触边沿的距离。为了尽可能减小缓冲层电阻，可以适当增加n+层的掺杂浓度，或者减小阴极到阳极的距离。但是由于工艺限制，两者间距不易太小，否则由于欧姆合金爆点或者剥离残留等导致阴极阳极短接或两者间存在尖端放电而带来可靠性的问题。

(c)欧姆接触电阻Rcontact

欧姆接触电阻主要受到欧姆金属功函数和半导体电子亲和能之间的差值以及制作欧姆接触的工艺两方面决定。一般GaN的接触电阻在0.2 Ω·mm以下，比接触电阻率在10-6cm2量级，实际设计中阴极面积通常为几百μm2，此时接触电阻对总的电阻的贡献远小于1 Ω，基本可以忽视欧姆接触对总电阻的影响。

1.2 二极管的变容特性

结电容Cj公式如下:

式中:ε为外延层介电质常数;S为阳极面积。结电容大小主要受阳极面积以及外延层掺杂浓度影响，变容特性主要受掺杂浓度和外延层厚度影响。一般而言，在二极管工作电压波动范围内，二极管耗尽层宽度变化范围需要保证在外延层厚度范围内。因此在阳极面积不变以及肖特基势垒相同的情况下，最大电容在零偏时获得，主要受外延层掺杂浓度的影响;最小电容在外延层完全耗尽时取得，除了掺杂浓度外很大程度上取决于外延层的厚度。

1.3 二极管的频率特性

二极管的本征截止频率fc=1/(2 πRC)，由串联电阻和电容共同决定。而电阻和电容受外延层掺杂浓度Ne，阳极面积S的共同影响，外延层电阻还受外延层厚度Tepi的影响。通过提高外延层掺杂浓度可以减小电阻，同时也会增大结电容。通过公式(2)和(8)可以得出阳极直径为1 μm和外延层厚度Tepi。

在一定的情况下，本征截止频率和掺杂浓度的关系，如图3所示。

图3 本征截止频率与掺杂浓度关系Fig.3 Relationship between Intrinsic cut-off frequency and doping concentration

由图3可知，二极管的本征截止频率随着外延层掺杂浓度的增加而提升。但是考虑到高频条件下二极管的电容电阻的变化，实际情况与公式计算的会有一定差距。根据本文仿真结果来看，仿真得出的在300 GHz条件下的零偏结电容明显比公式计算所得要小，因此在不考虑电阻的变化情况下，由仿真结果得出的本征截止频率比理论公式计算的要大。

2 器件的结构设计

2.1 外延层恒定掺杂结构

器件结构采用Sentaurus SDE模块模拟。最底层为AlN成核层;在成核层上是厚度为2 μm的n+GaN重掺杂层，其n型的恒定掺杂浓度为2×1019cm-3;n+GaN层上为0.3 μm的n-GaN轻掺杂层，其恒定掺杂浓度为8×1016～5.5×1017cm-3;最上层为50 nm的SiN钝化层。阳极制作在n-GaN层表面，其边长为1 μm。阴极制作在n+GaN层表面，为降低接触电阻，阴极长度设为15 μm。

2.2 渐变掺杂结构

采用高斯掺杂分布。外延层上表面掺杂浓度为2.5×1017～5.5×1017cm-3， 外延层下表面掺杂浓度取比表面小的数值。掺杂浓度由上表面渐变减小过度到下表面，为高斯因子为0的高斯分布。

2.3 物理模型的定义

由于二维仿真无法实现圆形阳极，为此定义了器件的栅宽为1 μm近似代替阳极尺寸。栅接触金属使用Ni/Au工艺，参考实际Ni/Au工艺下的肖特基势垒高度，把仿真的肖特基势垒高度设为1.2 V。阴极长度设为15 μm，仿真的欧姆接触肖特基势垒高度为0.05 V，使得接触为理想的欧姆接触。

3 器件的电参数结果分析

3.1 C-V 关系

根据相关报道可知，当外延层为0.3 μm，漏电流密度为10-8A/μm2时器件的工作电压可达到-18 V[2]。在外延层为恒定掺杂的情况下，反偏电压从-16 V扫描到0 V得出掺杂浓度从1×1017～5×1017cm-3变化的C-V曲线如图4所示。

图4 恒定掺杂时的C-V关系Fig.4 Relationship between capacitance and voltage with constant doping

由图4可见，当掺杂浓度较低时，电容C随着电压V的增加快速减小，在电压没到-16 V时其变化率已经很小。随着掺杂浓度的提升，电容C最大值变大而且电容变化率在接近-16V时没有明显减小。主要是由于在电压未到-16 V时，较低掺杂浓度的外延层已经处于耗尽状态，因此随着电压升高电容变化很小，而掺杂浓度高时，在此电压下外延层并没有完全耗尽，还会随着电压的增加而继续耗尽，进而导致电容随着耗尽层宽度变宽而减小。结合耗尽区宽度图可知，当耗尽区宽度等于外延层宽度时，最适宜的掺杂浓度为2.5×1017～3×1017cm-3。

保持外延层厚度不变，掺杂方式改为渐变掺杂时得出的C-V曲线随掺杂浓度变化的关系如图5所示。由图5可见，当表面掺杂浓度一样时，底部掺杂浓度高的电容较大，主要原因是浓度梯度较小使得零偏时耗尽区内包含的电荷量更多，进而导致电容较大。同时当表面掺杂浓度一样时，底部掺杂浓度越低，电容的变化范围越大。

图5 渐变掺杂时的C-V关系Fig.5 Relationship between capacitance and voltage with changed doping

3.2 C-V-f关系

电容除了和掺杂、电压有关，还和工作频率有关。通过仿真发现，随着频率的提高，电容值减小明显，而且电压越接近零时，电容随频率的变化越明显，表明电容的变化减弱，这不利于谐波的产生，将对高频下的倍频效率带来负面影响，如图6所示。

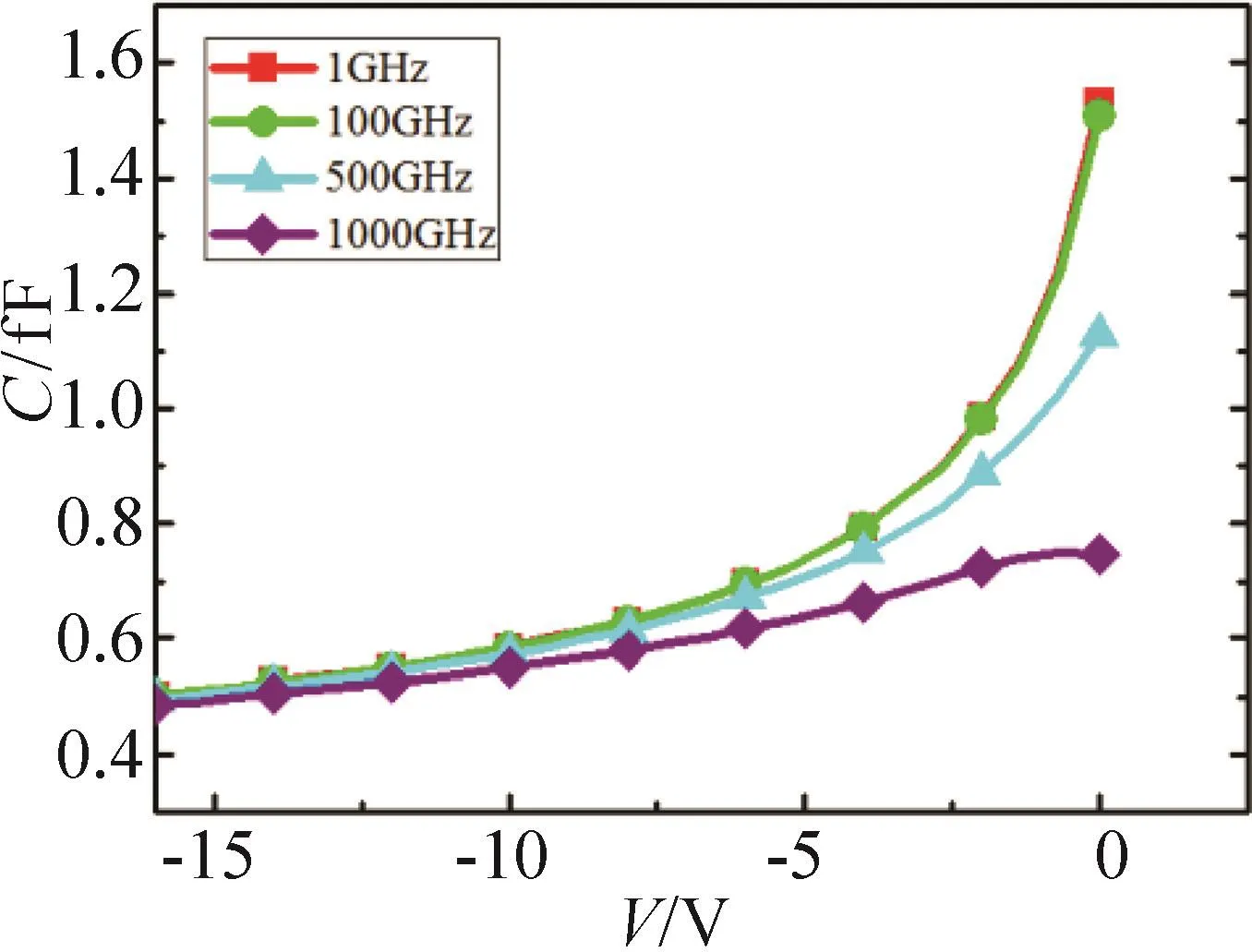
图6 C-V关系随频率的变化趋势Fig.6 The trend of the relationship between capacitance and voltage with frequency

3.3 倍频效率与C-V曲线之间的关系

由傅里叶变换相关原理可知，当信号的陡增陡降越明显，信号中包含的谐波分量越丰富。因此二极管C-V曲线变化越剧烈，导致感生电流变化越剧烈，从而使信号中包含的谐波分量越多，倍频效率进而得到提高。根据相关研究表明，SBD的C-V非线性越强，则其倍频效率越高[2]。

倍频效率计算详细步骤如下:

(1)设定阳极偏置电压为-8 V，加频率为300 GHz，幅值为8 V的正弦电压信号;

(2)通过仿真工具获取此激励下的C-V曲线;

(3)根据公式Q=C(Vb)·Vb求出电荷量的曲线;

(4)根据公式i=∂Q/∂t求出电流曲线;

(5)通过数字滤波求出各频率分量电流.

(6)根据以下公式求出i次谐波的倍频效率。

式中:P(total)为二极管两端的总功率，Px(R)为感生电流的x次谐波在电阻上消耗的功率，Px(ω)为感生电流的x次谐波在二极管两端的功率。由于总功率P(total)里面包含了串联寄生电阻消耗的功率，以及实际情况下存在反偏漏电，因此串联电阻越大倍频效率越低。考虑到二极管串联电阻的分压作用，实际加在结两端的电压幅值应该比16 V小。但是由于此时结电容的感生电流为几十毫安量级，实际的分压值相对工作电压较小，为便于计算用二极管两端的电压代替结电容两端的电压。在做了如上近似后得出在最大电压为-16 V时的Cmax/Cmin、倍频效率和掺杂浓度的关系如图7、图8所示。

图7 Cmax/Cmin和掺杂浓度的关系图Fig.7 Relationship between Cmax/Cminand doping concentration

在仿真范围内且认为器件无击穿的前提下由图7和图8可知:

(1)当外延层恒定掺杂时，随着掺杂浓度的提高，Cmax/Cmin变大，二倍频的效率提高，倍频效率最高可达32.5%。但是三倍频的效率先增加然后略微减小后再增加。当掺杂浓度变大后变化趋势变慢，基本达到饱和，稳定在16%左右。因此，理论上三倍频效率远低于二倍频，且约为二倍频的一半。

图8 倍频效率和掺杂浓度的关系图Fig.8 Relationship between frequency doubling efficiency and doping concentration

(2)当外延层为渐变掺杂时，在表面掺杂浓度大于2.5×1017cm-3时，掺杂的浓度梯度越大，Cmax/Cmin就越大，同时二倍频和三倍频的倍频效率也就越高。在表面掺杂浓度等于2.5×1017cm-3时，Cmax/Cmin以及二倍频的效率并不在掺杂浓度梯度最大处取得。但是三倍频的倍频效率在掺杂浓度梯度最大处取得。

(3)渐变掺杂的最大倍频效率高于恒定掺杂的值。在渐变掺杂浓度为5.5×1017～1×1017cm-3时的二倍频效率比恒定掺杂为5.5×1017cm-3时提高了51%。在渐变掺杂浓度为2.5×1017～1×1017cm-3时的三倍频效率比恒定掺杂为2.5×1017cm-3时提高了50%。在仿真的掺杂范围内，二倍频最大效率可以达到49%，三倍频最大效率可以达到23%，分别较恒定掺杂提高了58%和44%。

对以上情况作如下分析:

根据仿真结果来看，在恒定掺杂时二倍频和三倍频的倍频效率随掺杂浓度的变化趋势并不一致;在渐变掺杂时，当渐变掺杂的表面掺杂浓度小于2.5×1017cm-3时，二倍频和三倍频的倍频效率随掺杂浓度梯度的变化关系也不一致。为了解释以上现象，需要做进一步的理论分析，分析过程如下:

设输入为正弦波:V=Usin(ωt)。根据C=f(V);Q=V·C;i=∂Q/∂t。 当电容和电压成非线性关系时，既:C(V)=aV0+bV1+cV2+…+mVn则电流为:

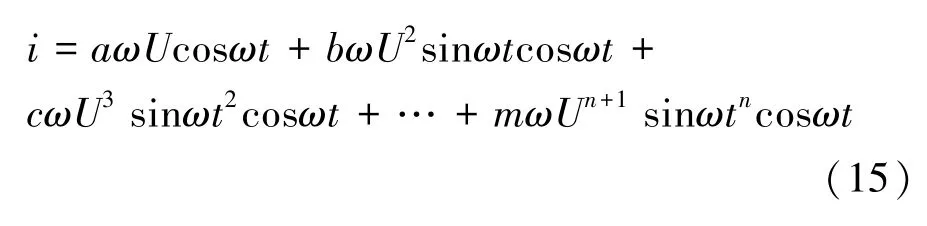
根据时域频域变换时有时域相乘等效于频域相加的原理，当输出电流只包含二倍频或三倍频时，对应多项式为bV1或cV2。也就是说当C-V之间的关系越接近一次函数，则其二倍频效率越高。当C-V之间的关系越接近二次函数，则其三倍频效率越高。由此可见，x倍的倍频效率并非只随着非线性的强弱而增强，而是随着C-V关系更接近x-1次函数而增强。

为验证以上分析的合理性，取变化规律较特殊的几组数据进行进一步分析，使分析结果更具有一般性。选取渐变掺杂浓度为2.5×1017～1×1017cm-3，恒定掺杂浓度为1×1017cm-3和2.5×1017cm-3的三组数据，通过对C-V求一阶导数和二阶导数，对以上推断加以佐证。一阶导数和二阶导数的图如图9和图10所示。针对二倍频的倍频效率对比做如下分析:

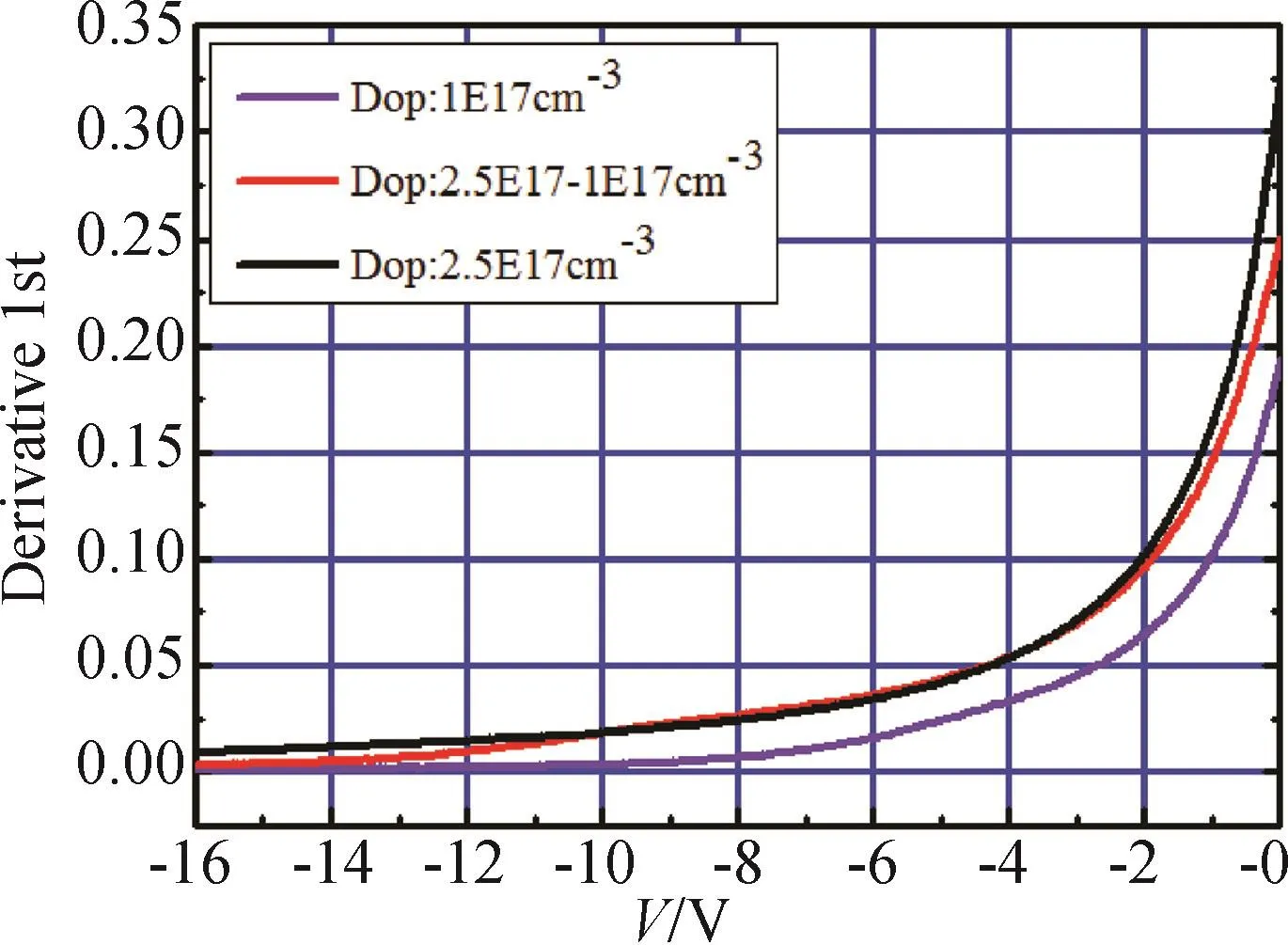
图9 C-V关系的一阶导数图Fig.9 The first derivative of the relationship between capacitance and voltage

由图9所示，当V小于-4 V时一阶导数变化较小，近似将此电压范围内C-V关系视为一次函数。在此电压范围内掺杂浓度为2.5×1017cm-3的一阶导数值最大，使得在此电压范围内的二倍频效率最大。当V大于-4 V时，三组数据的C-V非线性都很强，可视为对各高次谐波的贡献率相等。因此在整个工作电压内恒定掺杂浓度为2.5×1017cm-3的二倍频效率最高，恒定掺杂浓度为1×1017cm-3的二倍频效率最低，结论与计算出的倍频效率相吻合。针对三倍频效率可做如下分析:

图10 C-V关系的二阶导数Fig.10 The second derivative of the relationship between capacitance and voltage

如图10所示，当V小于-4 V时三者的二阶导数都几乎不变，近似将此电压范围内二阶导数不为零的C-V关系视为满足二次函数关系。由图中可知在此电压范围内掺杂浓度为2.5×1017～1×1017cm-3的渐变掺杂器件总体而言具有最大的二阶导数，因此具有更大的三倍频效率，恒定掺杂浓度为2.5×1017cm-3和1×1017cm-3的器件三倍频效率依次降低。当V大于-4 V时三组数据的C-V非线性都很强，可视为对各高次谐波的贡献率相等。因此在整个工作电压范围内结论与计算出的结果相一致。

综合以上对C-V曲线公式推导以及对导数的分析来看，两者结论一致，并且符合实际计算出的效率变化趋势，因此以上分析具有一定合理性。

3.4 倍频功率与掺杂浓度之间的关系

通过以上分析可知渐变掺杂能够提高倍频效率，但是其效率的提升能否带来倍频功率的提升还需进行一步分析。

倍频功率随掺杂浓度变化的趋势如图11和图12所示。

由图11可知:

(1)对于恒定掺杂的变容二极管，其总功率随着掺杂浓度的增加先减小后增加。在仿真范围内其最大功率40.8 mW在掺杂浓度为5.5×1017cm-3处取得;最小功率30.7 mW在掺杂浓度为2×1017cm-3处取得。

(2)对于渐变掺杂的变容二极管，在仿真的几组数据中表现为:当表面掺杂浓度大于2.5×1017cm-3时，其总功率大致随着底部掺杂浓度的增加而增加;当表面掺杂浓度等于2.5×1017cm-3时，表现为总功率随着底部掺杂浓度的增加先略微减小然后增加。

图11 总功率和掺杂浓度的关系Fig.11 Relationship between total power and doping concentration

图12 倍频功率和掺杂浓度的关系Fig.12 Relationship between power of frequency doubling and doping concentration

由图12可知:

(1)对于恒定掺杂，其二倍频功率随着掺杂浓度的增加而增加，在仿真范围内最大为13.3 mW，最小为1.4 mW;其三倍频功率随着掺杂浓度的增加先增加后减小，在仿真范围内最大为6.6 mW，最小为2.6 mW。

(2)对于渐变掺杂，当表面掺杂浓度大于2.5×1017cm-3时，其二倍频功率随着底部掺杂浓度的减小而增大。当表面掺杂浓度小于2.5×1017cm-3时，其二倍频功率随着底部掺杂浓度的减小而减小。当表面掺杂浓度大于2.5×1017cm-3时，变容二极管的三倍频功率基本保持在6 mW左右。当表面掺杂浓度小于2.5×1017cm-3时，其三倍频功率随着底部掺杂浓度的减小而增大，最大为6.7 mW，最小为4.6 mW。

(3)结合图8、11、12来看，在仿真范围内在表面掺杂一定时，恒定掺杂的二极管总功率比渐变掺杂的有优势。但是由于渐变掺杂的二极管倍频效率较高，进而导致渐变掺杂的变容二极管倍频功率反而比恒定掺杂的要高。

4 结论

本文基于Sentaurus仿真工具对恒定掺杂和渐变掺杂的GaN太赫兹肖特基变容二极管进行了仿真研究。依据仿真数据，计算出器件在不加外围电路时的二倍频和三倍频的倍频功率和效率，得出了倍频效率与倍频功率与掺杂浓度以及掺杂方式之间的关系。同时，通过公式推导和实际数据计算分析，对掺杂浓度与倍频效率功率之间的关系变化趋势做了合理解释。本理论研究得出的相关结论将为未来器件的设计打下理论基础。后期，将根据仿真结果进行实际的器件制备，并匹配相关外围滤波电路对仿真结果进行验证，通过理论与实际相结合的方式推动GaN太赫兹倍频二极管的研究与发展。