数形结合解数学题

文 西安高新第一中学高三（6）班 张筱溪

数形结合巧妙地将直观的空间图形与抽象的数量关系有机结合，其实质是数与形的相互转换，是数学解题中不可或缺的基本策略。

我在数学解题中重视数形结合思想的应用，优化了解题途径，提高了解题效率。

一、由“数”想“形”，以“形”助“数”

对于某些数学问题，其代数式在变形之后往往有一定的几何意义，如代数中的二元一次方程与几何中直线的截距紧密相联，比值则与两点连线的斜率息息相关。

我在解题过程中，注重思考由“数”想“形”，以“形”助“数”，常常将代数问题几何化，将抽象问题转化为更加直观的问题，从而快速找到解题的突破口。

例1：若方程2+2 +=0的两个实根在方程2+2 +-4=0的两根之间，试求参数 与 应满足的关系式。

解析：画出2+2 +=0和2+2 +-4=0对应的二次函数1=2+2 +，2=2+2 +-4的图象，如图1。

图1

观察该图象可知，这两个函数图象均为开口向上，形状相同，且存在公共对称轴的抛物线。要使方程2+2 +=0的两个实根在方程2+2 +-4=0的两根之间，意味着与其对应的函数图象1与 轴的交点应在函数2与 轴的交点之内，相当于抛物线1的顶点纵坐标应小于或等于零，且大于抛物线2的顶点纵坐标。

由配方法可知，抛物线1和1的顶点分别为 （1-,-2+），（2-,-2+-4），所以-2+-4≤-2+≤0，从而求出 与 应满足的关系式为 -4≤ ≤0。

二、由“形”化“数”，以“数”解“形”

对于某些几何问题，若直接利用几何方法求解不易入手，我会观察图形，分析已知条件和所求目标的特点，由“形”化“数”，以“数”辅“形”，将题目中的图形用代数式表示出来，使几何问题代数化，从而化难为易。

例2：已知 A、B为平面上的两定点，C为平面上位于直线AB同侧的一个动点，分别以AC、BC为边，在ABC 外侧作正方形CADF、CBEG ，求证：无论C点取在直线AB同侧的任何位置，DE 的中点M的位置均不变。

分析：由于D、E随着C的变化而变化，但M为定点，故用几何方法求证难度较大，此时若能转换思维，以“数”解“形”，以C点坐标为参量，以AB的中点为坐标原点，建立复平面，证得 点坐标不随C点的变化而变化，即可以使问题迎刃而解。

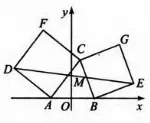
图2

证明：以的中点为坐标原点，直线为实轴，建立复平面，如图2所示。设对应的复数分别为，其点的坐标为同理，可得 点的坐标为根据中点公式，可知的中点的坐标为（0，a），它只与的长度有关，与点位置无关的点，所以，无论点取在直线同侧的任何位置，的中点的位置均不变。

总之，在平时数学解题中，我比较注重灵活渗透数形结合的思想，尽量运用数形结合的方法解题，从而学会从形的直观性和数的严谨性两方面思考和分析问题，使代数问题几何化，几何问题代数化，复杂问题简单化，抽象问题直观化，久而久之不但开拓了解题思路，而且优化了思维品质，提升了数学解题能力。