复杂化学反应体系配平的“元素基向量”法
2019-01-12廖荣宝金凤金晓艳王畅师瑞娟刘俊龙冯彩红唐剑周俊东汤忠斌
廖荣宝,金凤,金晓艳,王畅,师瑞娟,刘俊龙,冯彩红,唐剑,周俊东,汤忠斌
( 1. 阜阳师范学院 化学与材料工程学院,安徽 阜阳 236000;2. 阜阳师范学院 数学与统计科学学院,安徽 阜阳 236000)
化学反应方程的配平是化学研究涉及的问题之一[1-5].但复杂反应体系的配平通常无法通过初等数学方法解决.例如,含H2、O2、H2O、CO、CO2、CH4、HCHO、CH3OH、C2H5OH、CH3CHO和(CH3)2CO共11种化学物质的体系,该体系中任何一种物质都可能是反应物或生成物,体系包含无数种可能存在的反应方程.这样的反应体系采用基于初等数学知识的常规方法,如观察法[6,7]和电子计量法[8-11]等,无法配平.
对于复杂反应体系,往往需要先考察体系有多少独立反应[3],但常规配平方法无法求算出体系独立化学反应的数量.为此,需要采用抽象的高等数学工具来处理这类复杂化学反应体系的配平问题.目前,复杂化学反应体系方程的配平有且仅有一种方法,即矩阵法[12,13].但矩阵法概念抽象,不利于把配平过程和直观理解关联起来.
为避开矩阵法过于抽象的缺点,本文提出了“元素基向量”法.在元素基向量法中,各元素(或电荷)被看作自然基,简称元素基向量(为方便表述,本文中电荷自然基也被统称为元素基向量).体系的全部元素基向量张成一个空间.化合物由元素线性组合构成,因此体系的每类化合物都对应空间的一个向量.在不考虑异构体的情况下,向量与化合物有一一对应关系.为简化讨论,本文把异构体视作同一化学物质.此外,本文中无论离子、分子(或单质)、电荷,都统称为化学物质,并略去反应式的气体和沉淀符号.
1 元素基向量法简介
1.1 元素基向量的引入
设体系含H+、OH-、H2O 3种物质.不难发现该体系涉及O、H以及电荷共3种要素.该体系的任意化合物均可由这3种要素组合得到.例如,OH-和H+可分别写为(1)式和(2)式.设三维空间有3个自然基a、b、c,则三维空间中的任意向量均可由3个自然基通过线性组合得到.因此,若把O、H、e+分别与三维空间的自然基a、b、c对应起来,则H+、OH-、H2O均可看作向量.
OH-=O+H-e+
(1)
H+=H+e+
(2)
依据这一思想,在一个不含带电离子的反应体系中,每种元素都对应一个元素基向量.假设体系含h种原子,则对应的h个元素基向量构成一个h维空间,每个化合物都是这个h维空间中的一个向量.若体系含有带电离子,则需额外增加一个对应于电荷的元素基向量(电荷元素基向量写为e+),因此体系增加一个维度.现假设体系维度是n(有n个元素基向量),则体系中任意化合物、单质或离子都可由n个元素基向量线性组合得到.若这个n维空间中含m种化学物质,则这m种化学物质可视为n维空间的m个向量.
1.2 独立反应数和反应分类
体系的m种化学物质可能线性相关,也可能线性无关.假设这m种化学物质中最多含p种线性无关的化学物质,则必有p≤m.实际上,可用p种线性无关的化合物向量构建其他m-p个化合物向量,每个化合物向量的构建过程都对应一个独立反应.因此,体系的独立反应数为m-p.此外,若体系维度是n,则最多存在n种线性无关的化合物,因此p≤n.考虑到n、m和p的大小关系,有如下3种情况.
情况1,p=m.此类情况包含两种情形.其一是p=m
情况2,p=n H++OH-=H2O (3) (4) 在以上情况2中,p=n.被选定的p种线性无关的化合物可看作由n个元素基向量线性组合构成.那么反过来,n个元素基向量也可由p种线性无关的化合物构成.据此,可首先选择p种线性无关的化合物,并用这p种化合物构建n个元素基向量.再用n个元素基向量构建剩余的m-p种化合物.这样就得到了m-p个独立反应方程. 以上情况3的3种情形的配平有一个统一的模式.情况3中p 以上即元素基向量法的基本思路.虽有些抽象,但实际操作并不复杂.接下来,本文结合案例分别讨论p=n和p 现给出元素基向量法配平一个已知反应物和生成物的反应方程的步骤.第一步:通过移项把待配平反应式的某一化合物移到方程左边(一般把较复杂的化合物移到左边有助于简化配平过程),把其他化合物移到右边.第二步:把移项后反应式右边的化合物看作初始化合物向量,并用初始化合物向量的线性组合构建各元素基向量对应的表达式.第三步:把反应式左边的化合物展开成各原子的线性组合,再分别代入第二步获得的各原子的元素基向量表达式,然后移项整理得配平后的反应式. 现以(5)式反应的配平为例说明元素基向量法的操作步骤.该体系有Al、H、O共3种原子,n=3,对应三维空间.有Al、H2O、Al(OH)3、H2共4个化合物,m=4.因此体系至少有1个独立化学反应.结合体系特征不难得出p=3,本例属p=n的情况. 第一步:把Al(OH)3移到反应式左边,其他化合物移到右边,得(6)式. Al+H2O→AlOH3+H2 (5) AlOH3→Al+H2O-H2 (6) 第二步:把(6)式右边的Al、H2O、H2看作初始化合物向量.用初始向量Al表达Al原子的元素基向量,如(7)式.用初始化合物向量H2表达H原子的元素基向量,如(8)式.用(9)式给出O的表达式,并用(8)式替换(9)式中的非初始化合物向量H后得元素基向量O的表达式(10).至此,元素基向量Al、H、O均被表达为初始化合物向量Al、H2O、H2的组合,如(7)、(8)、(10)式. 第三步:把(6)式左边的Al(OH)3展开成元素基向量组合形式(11)式.再针对(11)式右边的元素基向量Al、H、O带入其对应的表达式(7)、(8)、(10),整理后得(12)式. Al=Al (7) (8) O=H2O-2H (9) O=H2O-H2 (10) AlOH3=Al+3O+3H (11) 2Al+6H2O=2AlOH3+3H2 (12) (13) (14) 第二步:采用初始向量H2O、CO2、H+、H的线性组合构建体系的元素基向量表达式.初始向量H即为H的元素基向量,如(15)式.基向量e+可表达为(16)式.元素基向量O可表达为(17)式.现把元素基向量C写为(18)式,再采用(17)式替换(18)式右边的非初始化合物向量O得到元素基向量C的表达式(19).至此,获得了体系元素基向量H、e+、O、C的表达式,分别如(15)、(16)、(17)、(19). H=H (15) e+=H+-H (16) O=H2O-2H (17) C=CO2-2O (18) C=CO2-2H2O+4H (19) (20) (21) 复杂反应体系指含多种化合物的体系,如含HCHO、H2O、CO2、CO、H2、O2、CH4、CH3OH、C2H5OH、CH3CHO、(CH3)2CO共11种化合物的体系.该体系中有些化合物既可做反应物又可做生成物,可能存在的反应方程有无限多种.这类反应体系无法采用初等数学方法获得体系可能发生的独立反应数并一次性配平所有可能发生的反应. 以上反应体系中m=11.容易发现该体系含C、H、O共3种原子.体系化合物均不带电,因此n=3.可从11种化合物中找出3个线性无关的化合物,如CO、H2、O2,因此p=3.由此得出体系有8个独立反应.很容易用CO、H2、O2构建出C、H、O的元素基向量表达式.把除CO、H2、O2之外的8个化合物分解成C、H、O的加和形式,再带入C、H、O的元素基向量表达式即得8个独立化学反应.通过独立反应的线性组合可获得体系所有可能发生的反应. 复杂反应体系独立反应数的计算及方程配平是初等数学方法无法解决的问题.针对这一问题本文给出了元素基向量法,该法可处理任意复杂反应体系.元素基向量法有严谨的向量空间理论基础,有助于对反应本质的理解.相比矩阵法,元素基向量法更简明直观.
1.3 元素基向量的构建和配平思路
2 反应方程的配平
2.1 常规反应的配平举例
2.2 离子反应的配平举例
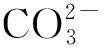
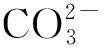
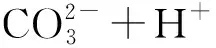
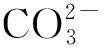
3 复杂反应体系的配平
4 结 论
