比例、数列、模度在版式网格体系设计中的运用与分析①

单筱秋（南京艺术学院 设计学院，江苏 南京 210013）

“网格”（Grid），又叫栅格或者网栅，瑞士设计师汉斯·鲁道夫·波斯哈德（Hans Rudolf Bosshard）在其经典著作《版面设计网格构成》（The Typographic Grid）一书中给予网格这样的定义：“一种安排均匀的水平线和垂直线的网状物”。“网格体系”（Grid Systems）则可以理解为网格构成或者栅格系统，其基本形式是由平面中垂直和水平划分而产生的区域和各个区域之间的间隔所构成。网格体系的主要特点是运用数字比例关系，通过严格的计算，对平面作出空间划分，从而指导和规范版面中视觉元素的布局以及信息的分布与排列。

网格体系形成的时间最早可以追溯到17世纪初法王路易十四（Louis XIV）在位期间，他曾命令成立一个专门管理印刷的皇家特别委员会，由数学家尼古拉斯·加宗（Nicolas Jaugeon）担任领导，这个特别委员会的首要任务就是设计出科学的、合理的、重视功能性的新字体，同时还提出了对新字体设计的要求：即以罗马体为基础，以方格的形式为设计基本单位，每个字体所占面积为64个大方格，每个大方格再细分成36个小格，这样一来一个印刷版面就是由2304个小格组成，在这个严谨的几何网格中，设计字体形状、编排版面、试验视觉信息传达功能的可能性。这是世上最早对字体和版面进行网格分割的实验性活动，也可以认为是网格体系的雏形。

网格体系在版式中的初步使用应该从德国人古腾堡所制作的“四十二行圣经”一书开始，在后来欧洲文艺复兴时期出版的各种书籍内页中也可以看到类似的网格体系版式编排。阿伯里奇·丢勒（Albrecht Dürer）是最早运用数学方法与几何学对版式设计进行一系列的探索的德国艺术家，1525 年他编写了关于设计理论的专著《量度艺术教程》（Instructions for Measuring with Compass and Ruler），在该书中，集中研究了包括螺旋线、蚌线和外旋轮线在内的线性几何结构和正多边形结构，他将这些几何学原理应用到建筑学、工程学和版式编排设计之中，尤其在编排设计部分，书中详细地讨论了如何运用构成原理、图形组合和几何比例的方法进行字体设计和图形色彩等版式设计的方法与技巧的实施。

到了20世纪初期，网格体系受到包括“未来主义”“达达主义”“风格派”“构成主义”以及包豪斯的影响，20世纪50年代，网格体系在前西德与瑞士受到广泛欢迎，尤其在瑞士的苏黎士和巴塞尔，设计师们努力探索网格体系设计，将其运用到报纸版式设计、书籍排版等各种领域，并通过瑞士平面设计杂志的宣传影响到世界各地。网格体系如今已经成为视觉传达设计领域最重要的基本设计技法之一，在其不断探索与发展中，艺术家和设计师们发现比例、数列、模数与网格体系秩序的形成息息相关。

一、黄金比例与黄金矩形

黄金比例（Golden Ratio）又称作黄金分割，黄金比例所运用到的领域相当广泛，尤其多体现在雕塑、绘画、音乐、建筑等领域。黄金比例主要体现在一条线段的分割上，线段的总长度为黄金比例的分母加分子的单位长度，把线段分割成两半，长的为分母单位长度，短的为分子单位长度，则短线长度与长线长度的比值就为黄金比例0.618：1。人类自古希腊开始就逐渐形成比例的观念和审美标准，矗立在雅典卫城最高处的帕特农神殿，在建造中采用的有关空间比例的分割手法就被认为是黄金分割的雏形。整个建筑呈长方形，东西宽31米，东西两立面的山墙顶部距离地面19米，也就是说其立面高与宽的比例为19:31，非常接近希腊人喜爱的“黄金分割比”。在19世纪初期，爱琴海的米洛岛山洞中发现了一座古希腊雕塑作品，这就是后来举世闻名的“断臂的维纳斯”。该雕塑由两块大理石巧妙拼接而成，总高203厘米，雕塑的上半身与下半身之比就拥有0.617的黄金比数值，匀称优美的体型给人以无限美感，现作为镇馆之宝收藏在法国的卢浮宫中。公元前6世纪古希腊数学家毕达哥拉斯（Pythagoras）认为“凡是美的东西都有共同的特征，这就是部分与部分以及部分与整体之间的协调一致”。他最早发现了1.618这一比例定律，后来古希腊美学家柏拉图（Plato）将此定律称为黄金分割，后又被称为“神赐的比例”。大自然中的许多事物，包括植物的叶片、花朵、雪花还有动物与昆虫的结构中都蕴含着丰富的黄金比关系，例如蝴蝶的身长与双翅展开以后的长度之比就十分接近黄金比例。

长宽之比为黄金分割率的矩形称为黄金矩形，矩形的长边为短边的1.618倍，它能够给画面带来美感，令人愉悦。达·芬奇就把黄金矩形引入了自己的绘画作品当中，例如在《最后的晚餐》中，犹大所坐的位置就处在黄金分割点上；在《维特鲁威人》中，以画面人物的头、足和手指各为端点，正好外接一个圆形，同时在画中清楚可见叠着另一幅图像：男子两臂平伸站立，以他的头、足和手指各为端点，正好外接一个正方形。一直以来，黄金分割律作为一种重要的形式美法则，成为世代相传的审美经典规律。黄金比例能实现最大限度的视觉和谐，可以让版面被分割的部分产生相互关联，因此也被视为最合理、最安定、最美观的版面划分形式。

二、斐波那契数列

斐波那契数列（Fibonacci Sequence），是以意大利数学家列昂纳多·斐波那契（Leonardoda Fibonacci）的名字而命名的数列。斐波那契数列是一种整数数列，从第三个数字开始，每一个数字都是前面两个数字相加之和，比如1，3，5，8，13，21，34，55，89……。它之所以重要，是因为随着斐波那契数的不断增大，相邻两个数的比值也会不断接近黄金分割的比值。依次以斐波那契数为边长的多个正方形按逆时针排列，可以不断地延展出新的矩形，由于正方形的边长与斐波那契数列相契合，所以每次产生的矩形也就愈加接近于黄金矩形。[1]如果在每个正方形里面画一个90度的扇形，连起来的弧线就是黄金螺旋线（Golden Spiral），也称“斐波那契螺旋线”。向日葵的种子数和鹦鹉螺的对数螺旋中都含有斐波那契螺旋线，被认为是自然界最完美的经典黄金比例。

斐波那契数列理论对后来现代主义设计思想产生了深远影响，无论是绘画中的构图还是建筑中的框架，都反映了人们希望通过秩序来整合杂乱信息的愿望。研究人员发现在达·芬奇的《蒙娜丽莎》中，画面人物的鼻子到下巴再到手的距离，就隐藏着斐波那契螺旋线。受到数学爱好者的追捧，斐波那契数列在西方影视艺术中也时常出现，好莱坞电影《达芬奇密码》中，斐波那契数列就是作为重要的符号和线索贯穿全剧；美国福克斯电视台播出的连续剧《危机边缘》更是多次将斐波那契数列引入剧情，甚至在该剧的宣传海报中也曾出现过它的身影。

斐波那契数列连接着自然法则和数学公式，可以指导我们在版面中分栏和进行信息的编排，将斐波那契数列应用于版面分割（图1），由34乘以55个单元格组成，内边缘留白5个单元格，外边缘留白8个单元格，底部边缘留白13个单元格，上部边缘留白8个单元格，得到矩形大小恰好为21乘以34个单元格，用这种方式来确定版心和图文的比例关系，可以让版面具有简单、统一、对称的性能，达到整体与部分之间的协调，从而获得和谐连贯的视觉效果，这种理性的数列规律带来的是版面赏心悦目的视觉感知。

图1 斐波那契数列应用于版面的分割

三、柯布西耶“模度”

瑞士建筑设计师勒·柯布西耶(Le Corbusier),作为20世纪现代主义建筑的主要倡导者和机器美学的重要奠基人，他认为“一个模数赋予我们衡量与统一的能力；一条参考线使我们能进行构图而得到满足”。坐落于法国东部索恩地区一座小山顶上的朗香教堂，是柯布西耶最具代表性的建筑作品，在朗香教堂落成的同时，柯布西耶完成了著作《模度》（Modulor）。朗香教堂是极具自由表现力的、超乎常规常理的建筑设计，而《模度》一书则是关于度量体系的极度理性的研究，两者同时面世，意味着柯布西耶对于规则与反规则的深度思考。在《模度》中，柯布西耶致力于创建一套完整有效的度量体系来满足社会标准化生产的需要。柯布西耶利用欧洲传统美学中最为常见的“黄金比例”，依据数学逻辑与人体比例关系，以身高183厘米的人作为标准，选定下垂手臂、脐、头顶、上伸手臂四个部位为测量点，得到的数值分别为：举手高226厘米，身高183厘米，脐高113厘米和垂手高86厘米。他从“单位、倍数、黄金比”这三个基本关系出发，得到两组以黄金比0.618为比值的等比数列，分别称为红尺（Red Series）和蓝尺（Blue Series）,蓝尺的数值是红尺的两倍。［2］柯布西耶将数值与斐波那契数列相结合，由此发展出了一套全新的度量体系。“模度”是西方关于几何与比例传统美学思想的延续，这种几何与比例并非抽象数字和几何图形的表达，而是与人体直接相关联，可以认为是一种人文主义精神的体现。［3］将这套“模度”引入版式设计中，在边长为2.26米的正方形版面中，运用这套度量体系对其内部进行分割，划分出的块面与块面之间可以实现严密的拼接，组成四十八种不同的版面构成形式（图2）。在“模度”的认识上，柯布西耶一直强调“模度只是工作的工具，一个精确的工具……如果用‘模度’产生了不和谐的事物，就暂时把它搁在一边，用眼睛去判断”。柯布西耶所创建的这套以人体为参考对象的“模度”测量方法虽然没能达到他最初用来满足社会标准化生产要求的设想，但是却成为版式设计网格体系初期重要的理论之一。

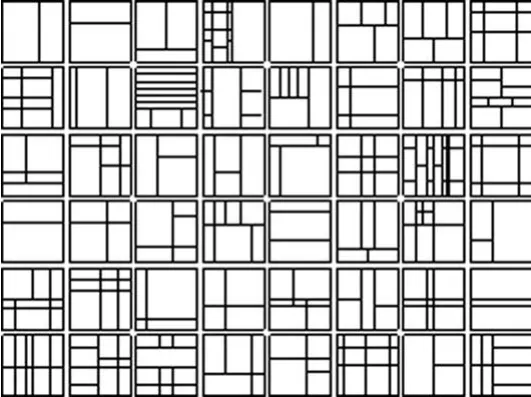
图2 在边长为2.26米的正方形中，“模度”体系可以将版面划分成48种不同形式

四、范德格拉夫版面构造原理

范德格拉夫(Van de Graaf)通过对古腾堡和其他书写人员所制作的书籍内页版式的研究，发现如果将版面均匀地分割成九等分，具有九分之一和九分之二的空白版面可以使文字区域的面积和整个页面的长宽面积具有相同的比例，即内部版心的边界长度是其对应的外部页面长度的一半,这种版面的划分比例被称作“范德格拉夫版面构造原理”（Van de Graaf Canon）。版面构造原理适用于任何比例的纸张，在许多中世纪的手抄本和古板书中都可以看到这样的版面分割形式。范德格拉夫发现一般情况下，如果纸张边长比例为 1:R，那么版心的边长比例就为1:R:2:2R，但是当纸张边长比例为 2:3 时，版心边长就会具有2:3:4:6(内边:上边:外边:下边)的整数比例（图3）。德国人扬·奇肖尔德（Jan Tschichold）在“范德格拉夫版面构造原理”的基础上细化了版面的网格分隔，他认为基于范德格拉夫所提出的九等分版面构造原理，特别是当纸张尺寸比例为2:3的时候，文字区域和纸张将具有相同的比例, 并且文字区域的高度等于纸张的宽度，这个时候的页面看上去最简洁明了，文字段落的编排与版面空间也会达到最佳的视觉和谐关系。奇肖尔德的这一发现与应用被写在《书籍的形式》（The Form of the Book）一书中，作为版式网格体系设计经典案例被广泛推广，一直沿用至今。

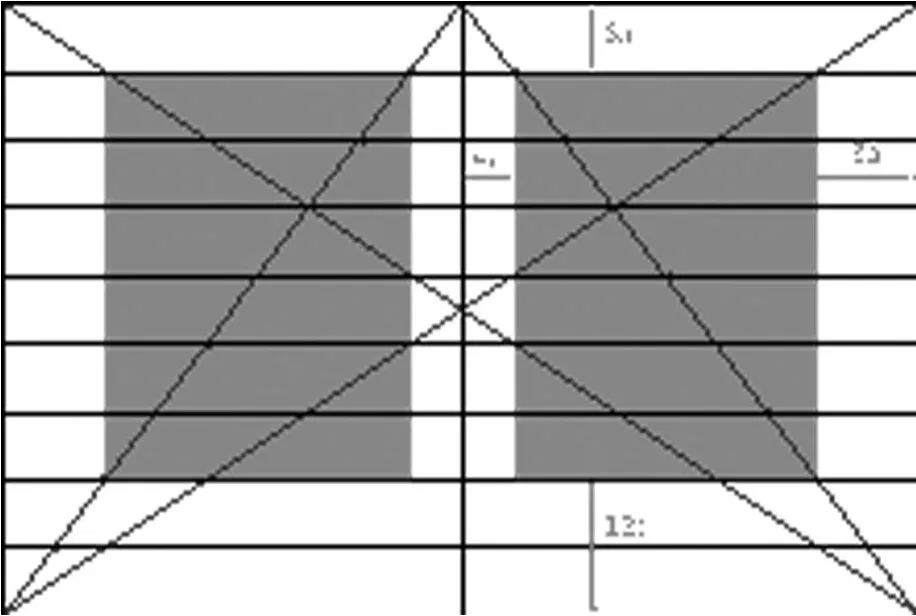
图3 把页面分成九个同等间距的水平网格，同时可以看到内外页边距和上下页边距的比例分别为2∶4∶3∶6

从古希腊时期人们对于自然界中黄金分割比例的发现与探索，再到斐波那契整数数列在版面中的应用研究；从柯布西耶的人体模度测量体系对早期版面网格体系理论的影响，再到奇肖尔德根据范德格拉夫九分版面构成原理所得出的纸张与版心的最佳视觉整数比，这一切都说明人们对于比例、数列等各种数学度量方法在网格体系中的探究与应用从来没有停止过。如今网格体系已经发展成为版式设计中最重要和最常见的基本设计技法之一。有效的网格体系原理的应用，可以帮助设计师通过数字化系统化的空间划分方法来明确版面结构与形式，构建良好的网络骨架，在各种设计要素之间建立起关联性和可持续性。能够在版面具有高度逻辑性的前提下，把混乱的、无序的信息通过网格体系变成清晰的、有序的、易于理解的信息，最终提高版面的易读性，达到有效传递信息的功能和目的。