数学认知视野下的群体互动场效应

□王文玲

（杭州市余杭区仁和中学，浙江杭州 311107）

学生获得数学基础知识、体会感受数学思想观念、运用数学方法解决实际问题、将数学基础知识进行深加工并迁移的过程，都属于数学认知范畴.学生在数学课堂上的认知过程中常常形成心理力场[1].教师在充分了解并牢牢把握学生内在心理力场的基础上，运用有效的群体互动建构外在心理力场，使群体互动场效应发挥积极的作用.

一、从知识点认知下看群体互动场的蝴蝶效应

蝴蝶效应是指在原创前提下的某一系统中，即便是细微的变动都能使整个原创系统发生复杂的长久的系列反应.在数学课堂教学这个群体互动中就常常能体现蝴蝶效应.学生的学习过程离不开学生自主思索、合作交流，当然教师富有启发性的传授，也能有一蹴而就的效果.如果能够将“自主探索”“教师引导”“生生互动”三者有机地结合在一起，就一定能使教学取得更为显著的效果.数学知识点是数学认知的主要对象，“形”（几何）与“数”（代数）是中学数学中两个紧密联系的研究对象.《从勾股定理到图形面积关系的拓展》这一内容，是学生已学习了的勾股定理及其逆定理，而勾股定理到图形面积关系的拓展，是图形与代数完美的结合，通过观察图形，探索图形间的关系，发展学生的拓展性思维、互助意识和研究精神.

师生回顾勾股定理，教师顺势引导学生理解勾股定理与正方形面积之间的关系，即以直角三角形的三条边分别作三个正方形，得到两个小正方形的面积之和便是大正方形的面积.如图1.

图1

师：如果将图1中的一个正方形对折，另外两个不变，是否存在S1+S2=S3？

师：那么怎么做才能使得S1+S2=S3仍然成立呢？

生2：将其他两个正方形按同样的方式对折.

师：如果以直角三角形的三条边a,b,c为边，向外分别作其他图形，那么是否存在S1+S2=S3呢？以小组为单位合作讨论完成.

组1：我们组是以直角三角形的三条边a,b,c为直角边，向外分别作等腰直角三角形，存在S1+S2=S3.

组2：我们组是以三条边向外分别作正三角形，存在S1+S2=S3.

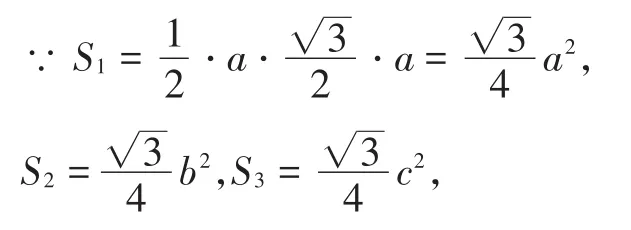
组3：我们组是以直角三角形的三条边a,b,c为斜边，向外分别作等腰直角三角形，存在S1+S2=S3.

组4：我们组是以直角三角形的三条边a,b,c为直径，向外分别作半圆，存在S1+S2=S3.

师：观察以上结果，你发现了什么结论？

生：以直角三角形的三条边a,b,c为边，向外分别作形状相同、大小不同的图形，存在S1+S2=S3.

在本节课的教学过程中，采取以小组为单位合作讨论的方式进行，因为每个学生都有自己的想法，一起画图、讨论、交流，从自己亲身参与的在认知面积法证勾股定理这一知识点活动中，体验数形结合的思想，从而培养学生的发散思维，产生积极的效应.教师恰到好处的引导探讨过程，从最基础的四边形到丰富多样的其他图形体现从特殊到一般的探讨方法.在知识的传播过程中抓住生长点，利用“蝴蝶”的力量，着力激发有效的“蝴蝶效应”，提升课堂的教学质量与学习效率.

二、从数学思想认知下看群体互动场的共振效应

共振效应最初指物理学范畴，两个振动频率相同的物体，当其中一个发出振动时，另一个引起振动.在数学课堂教学这个群体互动场中的共振效应是指：群体有了共同的目标导向，即数学思想，并采取相互协调、步调统一的集体行动，这种相互促进的集体行动又形成强大的动力，使个人和群体的行动越发有效.在课堂上，教师能够集中学生的积极要求，并根据这种要求积极努力开展教学工作，能在教学中产生积极的共振效应.

例如浙教版《数学》八年级上册第三章第三节《3.3一元一次不等式（1）》是进一步掌握一元一次不等式的基本概念和基本解法，本课内容在本章节乃至整个初中数学阶段都具有举足轻重的地位，在学生早已研究了不等式的基本性质之后，又为一元一次不等式组等知识的深造奠定良好基础，这一过程不仅是对已学知识的运用，还为后续的深入学习打下了基础.本节课的引入给学生留下深刻的第一印象，通过鲁班造锯体现数学中常用的类比思想，激发学生学习本节课的浓厚兴趣，同时这种类比思想有利于在文化底蕴领域发挥重要作用，大数学家欧拉就是运用了类比思想，解决了世界上著名的难题“巴塞尔”.在教学一元一次不等式概念和解法这个知识点时，创设宽松民主的学习气氛，激发学生思维的主动性，给学生充分的自主探索的时间和空间，引导学生建立新知与已有的知识的联系，以此减少学生获取新知识的难度，通过教师启发性的引导，调动学生学习新知的浓厚兴趣，组织学生积极参与“探究—讨论—交流—总结”的学习活动过程，让每个学生都能动手、动口、动脑，培养学生多方的能力来打造理想的高效课堂，促进师生课堂群体互动场的共振效应的发生.

观察下列不等式：

（1）x＞4 （2）3x＞ 30

师：上面这些不等式有哪些共同特征？请将它们与一元一次方程比较.

生1：都有一个未知数x.

生2：未知数都是一次.

生3：都是整式.

学生细心观察分析，七嘴八舌地总结其都有的特征，通过观察、猜测、归纳、总结这一系列过程，培养学生类比一元一次方程概念来推理一元一次不等式概念的意识，提升学生自主分析各类问题、解决各类问题的各方面能力.

在学生自己参与教学活动认知了一元一次不等式的概念后，为了帮助学生能够类比解一元一次方程的一般步骤归纳解一元一次不等式的一般步骤，一个小小的题目解锁学生的记忆.

解下列方程和不等式：

（1）7x-2=9x+3

生：移项，得：7x-9x=3+2

合并同类项，得：-2x=5

（2）7x-2≤ 9x+3

生：移项，得：7x-9x≤ 3+2

合并同类项，得：-2x≤5

在刚开始做题时，要求学生写出每一步解题步骤的具体依据.教师引导学生类比归纳：解一元一次方程就是将其逐步变形为x=a（a为常数）的形式，而解一元一次不等式就是把不等式逐步变形为x＞ a（x≥ a），x＜ a（x≤a）和一元一次方程类似的形式.在教学过程中，本着重视过程、重视实践、主动建构、自主参与、突出应用的基本原则，从学生的已有认知出发，让学生主动建构新的认知结构，提升学生的归纳推理能力，形成良好的思维导向.对一元一次不等式的概念和解法这一新知，重点和难点的认知的突破，还可以利用数形结合思想，使学生原有对一元一次方程的概念和解法认知发生振动.这就是数学课堂上从思想认知下体现的群体互动场的共振效应.

三、从思维方法认知下看群体互动场的塔马拉效应

思维方法是数学本质所在.群体互动场的塔马拉效应是指对于墨守成规的习以为常的观念或事情倒过来思索的一种逆向思维方式.在一般课堂上，学生已经习惯于沿着事情发展的正方向去思考问题并寻求解决问题的方法[2]，但其实对于一些特殊问题，从问题本身出发推回到已知前提去考虑，或许会使解决问题的方法更便捷，甚至因此会有所发现，这就是逆向思维的魅力.

例如《平行线的性质（1）》主要经历“两直线平行，同位角相等”这一平行线的性质的探索过程，并且会用此性质进行一般的判断和推理，学会表述，是属于空间和图形领域的基础知识，为今后学习三角形全等、三角形相似、四边形等知识奠定了理论基础.本节课首先通过中国古代《路边苦李》的故事，作为一种逆向思维在数学学习中的体现，在教授平行线的性质时，教师采用引导探究归纳法，通过精心设计问题，引发学生浓厚的学习激情，在教师因势利导的引导下，学生通过自主合作、观察、发现、测量、猜想、交流、归纳，总结出平行线的性质，使数学教学成为教师指导下、学生自主探索的活动过程，并在思索中逐步形成自己的观点，培养学生擅于观察、勤于动手、勇于表达、乐于思考的学习习惯.

例如图2，梯子的各条横档互相平行，∠1=100°，求∠2的度数.

图2

师：请思考本题并说说解题思路.

生 1：∵AB//CD，∴∠1=∠3=100°，∴∠2=180°-∠3=80°.

师板书1：AB//CD（已知）

生2：想要知道∠2的度数，就要知道∠3的度数，因为AB//CD，所以∠3与∠1的度数相等，只需要知道∠1度数.

师板书2：要求∠2的度数

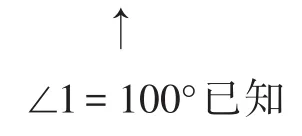
师：小组讨论这两种解题思路的特点.

生：思路1由已知条件出发，思路2由所求结果出发.

师概括：思路1的特点是从已知出发思考问题，由因寻果，为综合法.思路2的特点是从所求结果出发思索问题，执果找因，为分析法.

在教学过程中不难发现，整个班级大多数个体都比较平常，但有些学生擅长从已知条件出发去看待问题，有些学生则擅长从所求结果出发去看待问题，让他们的特长得以发挥，在解决问题的时候经常用两面夹击的方法，即用分析法去思索，寻找解题途径，用综合法进行书写，双管齐下，找到沟通已知条件和结论的最佳方法，逐步缩小条件和结论之间的距离.正如恩格斯所说：“没有分析就没有综合.”分析和综合既是对立的，又是统一的，相比较而存在的，这样就可以产生塔马拉效应.

综上所述，在课堂上，良好的学生群体互动关系会产生积极向上的能量，产生积极的互动效应，促进课堂教学工作积极有序的展开，并取得理想的效果.