基于θ映射法的燃气涡轮叶片高温蠕变变形分析
2019-01-11全昌彪廖明夫
全昌彪,廖明夫,米 栋,李 坚,刘 扬
(1.西北工业大学动力与能源学院,西安710072;2.中国航发湖南动力机械研究所,湖南株洲412002)
1 引言
高温工作构件在持续应力作用下,其蠕变变形逐渐累积,最终可导致构件塑性变形过大或蠕变断裂[1]。高温合金的蠕变变形与温度密切相关,工程上当温度达到材料熔点温度50%以上时蠕变就不能被忽略[2]。航空燃气涡轮发动机的强度设计准则中,对热端部件的蠕变变形、蠕变强度和蠕变/应力断裂寿命均加以了规定[3]。近年来,航空燃气涡轮发动机对高效率和高推重比/功重比的追求使得涡轮前温度不断提高[4],从而导致其热端部件(如燃气涡轮叶片/涡轮盘)因长时蠕变而导致的结构失效问题日益突出。因此,准确进行蠕变变形计算对航空燃气涡轮发动机热端部件的强度设计极具工程意义。
通常,恒定温度下构件受单轴恒定载荷发生的蠕变行为,可分为蠕变初始减速、蠕变恒速和蠕变加速三个阶段[2]。其中,第三阶段变形速率迅速上升导致最终失效,比较危险。传统的蠕变方程,如时间硬化理论和应变硬化理论,适用于蠕变的第一和第二阶段的分析计算。但工程实际中,由于温度、载荷的多变性,有些材料并不能明显体现出蠕变的三阶段划分,这就增加了蠕变计算分析的难度。要想准确描述蠕变的三阶段行为,θ映射法无疑为一种较好的选择。θ映射法是将蠕变变形描述为时间的指数函数[5],该函数的两个和式正好体现了蠕变减速阶段和蠕变加速阶段的叠加,而蠕变恒速阶段则体现了减速阶段和加速阶段之间的平衡关系。Brown等[6]采用θ映射法进行了蠕变变形计算,指出该方法可完整描述蠕变三阶段变形。Hayhurst等[7]应用θ映射法描述锻造合金钢1%Cr0.5%Mo0.25%V的蠕变行为,给出了拟合参数,其结果表明θ映射法在模拟高应力水平下的蠕变行为时比较接近实验数据。Ibanez[8]采用θ映射法对定向凝固合金GTD-111的蠕变行为进行了模拟,其工作表明θ映射法在模拟定向凝固合金的蠕变行为时,其内插性优良,而外推能力相对较差。
从本质上讲,θ映射法对材料蠕变力学性能的表征,是一种基于宏观连续介质力学的唯象方法,其数学模型没有考虑材料微观层次的变形机制,因此计算效率相对较高。然而,为实现三维结构的蠕变分析,还需要将宏观唯象的单轴本构拓展为多轴形式。鉴于此,本文按照Prandt-Reuss[9]塑性流动法则将θ映射法拓展成适合三维有限元分析的多轴形式,并进一步将其编制成UMAT用户子程序植入到ABAQUS有限元软件,对某型涡轴发动机涡轮叶片材料DZ408的纵向蠕变行为进行模拟计算。同时,对叶片在该型发动机60 h整机持久试车过程的蠕变行为进行近似模拟,并就计算所得叶尖位移量与3次整机60 h试车后的实测伸长量进行对比。
2 蠕变模型
2.1 单轴蠕变方程
对于各向同性材料,蠕变应变εc通常可表示为构件所受应力σ、温度T和时间t的函数,即:
如果给定试验条件(σ,T)时,蠕变应变只是时间t的函数:
Evans和Wilshire认为蠕变过程可描述如下[5]:
式中:θi(i=1~4)是与材料、温度及应力有关的常数。对于特定材料,θi可表示为应力和温度的函数:
式中:ai、bi、ci、di为材料特性相关的参数,可根据蠕变试验曲线进行优化获取。
2.2 多轴蠕变方程
由于θ映射模型的基本方程只是单轴的形式,而复杂结构一般都处于多轴应力状态,这就要求将单轴形式的本构模型向多轴形式拓展。多轴蠕变理论主要特点是考虑了变形与时间的关系,且随着时间的变化其蠕变规律会发生非线性变化。一般认为,多轴应力状态下蠕变模型满足以下基本假设[10]:①多轴应力状态下的蠕变公式必须可以退化成正确的单轴蠕变公式;②蠕变变形前后模型体积不变;③蠕变计算方程不受静水压力的影响;④各向同性材料的主应力和主应变的主方向一致。根据基本假设,塑性应力应变理论可类似在蠕变分析中推广应用。小变形情况下,蠕变应变率张量ε̇c服从Prandt-Reuss塑性流动[11]:
式中:λ为塑性乘子,Sij为应力偏张量,δij为Kronecker Delta函数,σkk为3个主应力分量之和。
由塑性理论分析可知,为确定式(5)中λ的值,根据单一曲线假设[12](硬化条件),多轴的等效蠕变应变率应和单轴的蠕变应变率具备相同的形式,则λ值由下式决定。
对式(3)求导,可得到蠕变曲线的斜率公式:
式中:为等效应力,其表达式如下:
将式(7)、式(8)代入式(5),则可得到多轴蠕变应变率的表达式:
3 蠕变模型参数的确定
DZ408材料在同一温度下进行了多种应力水平下的蠕变试验,表1汇总了其蠕变试验条件。本文根据其蠕变试验数据,采用最小二乘法按照式(3)和式(4)拟合出其中的蠕变参数,结果见表2和表3。

表1 DZ408材料蠕变曲线试验条件Table 1 Creep test conditions of DZ408

表2 θ参数拟合结果Table 2 Fitting results of parameterθ
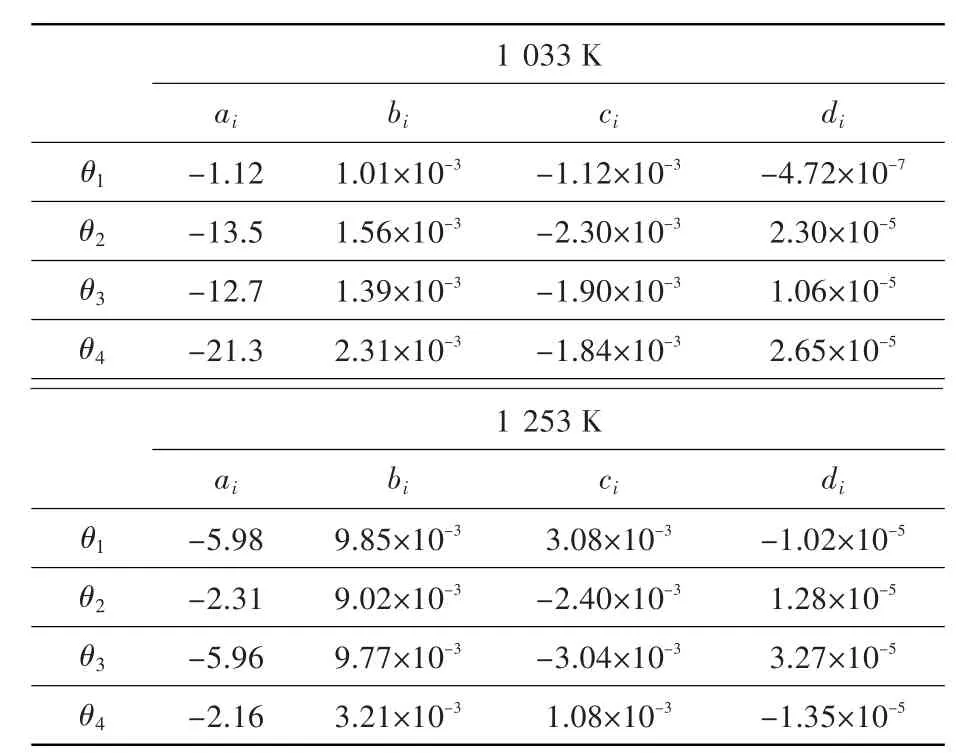
表3 a、b、c、d参数拟合结果Table 3 Fitting results of parametera,b,c,d
为获取蠕变曲线的拟合精度,验证模型参数的准确性,将2.2节多轴蠕变方程编制成UMAT用户程序嵌入ABAQUS有限元软件,采用体积胞元模型对DZ408材料纵向蠕变行为进行了数值模拟。图1给出了有限元计算曲线与试验曲线的对比,图中孤立点为试验曲线,实线为计算曲线。可看出,计算曲线与试验曲线较为吻合,验证了UMAT用户程序的正确性和蠕变模型方程的有效性。同时,由图1(a)可知,应力水平为540 MPa的计算曲线落在应力水平为530 MPa和550 MPa的两条试验曲线中间,说明蠕变模型参数能够适应内插。此外,从图1中蠕变曲线的特征还可看出:在较低的温度和相对较高的应力水平(图1(a))下,材料的蠕变曲线基本上没出现第三阶段;而在较高的温度和相对较低的应力水平(图1(c)和图1(d))下,材料在较短时间内就出现了第三阶段。由此表明,蠕变变形首先依赖于温度,其次是应力[13]。
4 算例分析
对某型燃气涡轮叶片60 h整机持久试车过程的蠕变行为进行了近似模拟。图2为简化处理后的叶片有限元网格模型。网格采用四节点四面体单元(C3D4)划分,共计148 582个单元,40 188个节点。
计算主要考虑了试车过程中不同载荷谱下的离心载荷和温度载荷。为模拟载荷的瞬态变化,在分析文件中定义了如表4所示的离心载荷和发动机动力涡轮前温度(T45)的历程,涡轮叶片的温度分布如图3所示。

表4 各分析步计算载荷Table 4 Calculation load of each analytical procedure
表5示出了给定计算载荷下,叶片在60 h蠕变过程中叶尖径向位移计算结果。卸载后叶尖残余变形量为0.086 94 mm。

表5 各分析步位移计算结果Table 5 Displacement calculation results of each procedure
从叶身根部至叶尖依次选取4个代表节点N913、N1978、N1833、N476,提取出其径向位移随时间的变化关系,见图4。从图中可看到,叶身的蠕变位移-时间曲线有明显的蠕变三阶段特征,从初始加载时的蠕变减速阶段,很快进入蠕变恒速阶段,接近60 h时又逐渐表现出蠕变加速阶段的特征。由此可知,涡轮叶片在较高的温度和离心载荷等的作用下,其变形与载荷不再是简单的一一对应关系,在载荷作用下还会随着时间的推移而逐渐增加。
叶片在整个蠕变过程中,叶身应力重新分布。图5给出了叶身中部位置N1341和N696节点当量应力随蠕变时间推移而发生的应力松弛现象。由图可看出,应力松弛现象使得叶身高应力区的应力有所降低,低应力区的应力有所增加,整个叶片的应力分布趋向均匀化,这有益于叶片的使用寿命。
5 计算变形与实测伸长量对比
卸载后叶尖的最大径向位移为0.086 94 mm。发动机在3次60 h持久试车后,涡轮叶片平均伸长量的实测值分别为0.058、0.083、0.080 mm,平均值为0.074 mm。计算结果与实测结果平均值相对误差约18.02%,其中有两次不到10.00%,对比结果见表6。

表6 叶片伸长量计算值和实测值对比Table 6 Comparison between blade elongation calculation results and test results
6 结论
(1)推导出的多轴形式的θ映射法蠕变本构模型,能较好地模拟高温合金DZ408材料的纵向蠕变特性。
(2)涡轮叶片发生蠕变后,其应力将重新分布,叶身的变形也会随着工作时间的推进而逐渐增加,在叶片蠕变变形设计和叶尖间隙设计时应予以考虑。
(3)采用多轴形式的θ映射法蠕变本构模型对某涡轮叶片进行三维蠕变分析得到的60 h叶片径向变形量与3次整机60 h持久试车后实测伸长量的平均值较为接近,平均值相对误差约18.02%,其中有两次误差低于10.00%。
(4)受材料仅有纵向蠕变试验曲线的限制,文中未考虑DZ408材料蠕变行为本身的各向异性,而是将其当作各向同性处理,这也是计算精度影响因素之一。此外,计算的叶片伸长量比3次实测平均值都要大,表明θ映射法在预测叶片的蠕变变形用于指导设计偏安全,可通过后续研究中持续积累试验数据与计算模拟逐步形成适用于工程应用的经验修正系数。
