灵活选择转轴解决大学物理中刚体的滚动问题
2019-01-10王永柱
【摘 要】刚体的滚动可视为质心的平动和刚体绕通过质心的转轴的转动两种运动的合成,也可以把滚动的瞬间看作刚体绕通过支点的轴的转动。本文分别选取这两种不同转轴对刚体的滚动问题进行解答。
【关键词】大学物理;刚体;平行轴定理
中图分类号: G642;O313.3-4 文献标识码: A 文章编号: 2095-2457(2019)35-0100-001
DOI:10.19694/j.cnki.issn2095-2457.2019.35.046
0 引言
物理学是研究物质的基本结构、基本运动形式、相互作用的自然科学[1]。以物理学基础为内容的大学物理课程,是理工科专业学生必修的一门基础课。大学物理中经常研究物体的运动规律,在解决同一问题时,由于解决途径的不同、研究方法的不同或者参考系的选取不同等,往往有多种解法。这种一题多解的方法在巩固和加深所学知识,培养学生发散思维能力与创新能力,培养学生学习兴趣方面起着重要作用[2]。例如同一个物理问题,解题时通过惯性系与非惯性系的灵活选取,既能简化问题,又能增进学生对知识的理解[3]。本文通过灵活选取不同的转轴,巧妙解决了教材中有关刚体转动的经典例题,有助于启发学生对物理问题的深入思考。
1 刚体滚动问题的两种方法
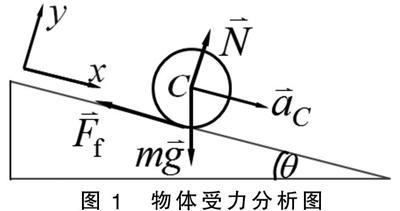
以教材中例题为例[4],如图1所示,斜面长l=1.5m,与水平面的夹角θ=5°。有两个物体分别静止地位于斜面的顶端,然后由顶端沿斜面向下滚动,一个物体是质量m1=0.65kg、半径为的实心圆柱体,另一物体是质量为、半径的薄壁圆柱筒。它们分别由斜面顶端滚到斜面底部各经历多长时间?
图1 物体受力分析图
解法一:物体由斜面顶端滚下,可视为质心的平动和物体绕通过质心的转轴所做的转动两种运动合成。由于圆柱体和圆筒的质量密度都是均匀的,因此他们的质心C都在轴线上。只因为两者的形状不同,故而他们的转动惯量并不相等。如图所示它们受到重力mg、支持力N、和摩擦力Ff的作用。由质心运动方程可得
mgsinθ-Ff=maC(1)
而以过质心C的轴为转轴,可由转动定律得
FfR=Jcα(2)
式中Jc和α分别为对通过质心C的转轴的转动惯量和角加速度。对刚体滚动来说。质心的加速度ac与圆柱体表面相对于转轴的加速度a相等,再由角量和线量的关系可得
a=ac=Rα(3)
(1)(2)(3)式联立可求得
a=■(4)
已知实心圆柱体相对于质心转轴的转动惯量Jc1=m1R2/2,圆柱筒的转动惯量Jc2=m2R2。把它们代入(4)式可得实心圆柱体的加速度a1和空心圆柱筒的加速度分别为
a1=2gsinθ/3,a2=gsinθ/2(5)
由匀变速直线运动的公式,容易求得它们到达斜面底部所经历的时间分别为
t1=■,t2=■(6)
由(5)式和(6)式,代入已知数据可求得:t1=2.3s,t2=2.6s。
解法二:物体滚下的任一瞬间,可以看做物体绕平行于质心转轴且穿过物体与斜面接触点的转轴(以下称转轴P)的转动。由于支持力N和摩擦力Ff均通过此转轴,因此这两个力的力矩为零。那么根据转动定律有
mgRsinθ=Jpα(7)
式中Jp、α分別为物体相对于转轴P的转动惯量和角加速度。
由于物体质心在其几何中心,则离转轴P为R,所以质心的加速度
α=Rα(8)
(7)式和(8)式联立可得
a=■(9)
根据刚体转动惯量的平行轴定理,若已知过质心转轴的转动惯量为Jc,则过任何与质心轴线相平行的轴线的转动惯量大小:J=Jc+md2,其中d为两平行轴之间的距离[5]。可得Jp=Jc+mR2。已知实心圆柱体相对于质心转轴的转动惯量Jc1=m1R2/2,圆柱筒的转动惯量Jc2=m2R2。因此有实心圆柱体相对于转轴P的转动惯量Jp1=3m1R2/2,圆柱筒的转动惯量Jp2=2m2R2。把它们代入(9)式可得实心圆柱体的加速度a1和空心圆柱筒的加速度a2,结果同(5)式一致。
由(5)式和(6)式,代入已知数据可同样可以求得:t1=2.3s,t2=2.6s。
2 总结
由于刚体的滚动既可以视为质心的平动和刚体绕通过质心的轴的转动两种运动的合成,又可以看作是刚体绕通过支点的轴的转动。以一种看法是两种运动的合成,因此解法一需要列出质心运动方程和转动定律两个基本方程,而解法二只需列出转动定律的方程,使解题过程大大简化。
【参考文献】
[1]非物理类理工学科大学物理课程教学基本要求[J].物理与工程,2006,16(5)
[2]郑艳彬.浅谈一题多解在大学物理教学中的作用[J].科技创新导报,2012(17):146.
[3]王永柱.力学问题的惯性系和非惯性系解法对比[J].高教学刊,2016(21):138-139.
[4]马文蔚.周雨青.物理学教程(第二版)上册[M].北京:高等教育出版社,2006:98-99
[5]田硕.刚体转动惯量的几种计算方法[J].中国西部科技,2015,14(06):82-84.