基于ANSYS软件PDS模块的压力容器可靠性分析
2019-01-10李文震徐征南
□ 李文震 □ 黄 思 □ 徐征南
华南理工大学 机械与汽车工程学院 广州 510640
1 研究背景
压力容器中的球罐,具有占地面积小、壳体受力均匀、承压能力强、现场安装和运输方便等优点,广泛用于石油、化工、冶金、城市煤气等领域[1-3]。同时,球罐作为压力容器中一种常见的薄壁压力特种设备,对安全和可靠性有着极其严格的要求。
目前,压力容器在选材、结构、计算等方面都已有一系列的标准规范。传统理论分析方法以材料力学为基础,将各设计参数视为常量进行计算,并用安全因数法校核。然而,压力容器在运行过程中,因工作载荷和工作环境的多变性,会出现裂纹及变形现象,严重时需要进行停产检修。此时,由于传统方法只用一个安全因数作为可靠性评价指标,判断依据通常比较保守,而且难以准确描述压力容器结构的应力应变行为。
随着有限元技术的飞速发展,有限元软件广泛应用于工程产品的可靠性分析、模型优化设计等方面[4-8]。ANSYS是目前较为通用的有限元软件,广泛应用于机械、土木、电子及航空等领域。ANSYS软件的PDS模块结合了有限元技术与概率设计理论,将各输入参数设置为符合一定分布规律的随机变量,在大量循环抽样计算后,不但能得出较为准确的失效概率值来评估用户对产品质量和可靠性的满意程度,而且可以得到输出参数对各输入参数的敏感性分析结果,从而在设计阶段可以做到有的放矢,根据敏感性程度对各输入参数进行合适控制,达到提高产品可靠性的目的。
张毅等[9]应用ANSYS软件PDS模块对液压支架顶梁进行可靠性分析,为液压支架的优化提供了科学依据。彭翠玲等[10]运用ANSYS的概率设计功能,对某压力容器进行了可靠性分析,获得了应力概率分布特征及压力载荷、壁厚等设计参数对应力分布的敏感程度。胡军[11]应用ANSYS软件PDS模块,对数控导轨磨床的主轴进行了可靠性分析,得到了比传统设计方法精度更高的主轴失效概率。
目前应用ANSYS软件PDS模块进行压力容器可靠性分析,大都只计算可靠性及各设计参数均值的灵敏度,未考虑各设计参数标准差的影响。笔者结合有限元技术和概率设计方法,以压力容器在役丙烷球罐为例,将其几何尺寸、工作压力及屈服强度等定义为随机输入变量,采用蒙特卡罗法和应力强度干涉理论,对压力球罐的可靠性进行分析,计算出较为准确的球罐可靠度,并探究各随机变量的均值与标准差的灵敏度分析结果。根据灵敏度分析结果,判断通过改变哪些参数来实现可靠性优化,对正确监测和判断压力容器的可靠性和安全状况,指导处于运转中的压力容器安全运行,具有重要的现实意义。
2 应力强度干涉理论
可靠度指产品在规定条件下和规定时间内,完成规定功能的概率,是衡量机械产品质量的一个重要指标[12-13]。应力强度干涉理论指在机械概率设计中,将载荷、强度、结构尺寸、工况等都视为具有变动性和统计特性的随机参数,构件所受的应力S和材料的强度Y均非定值,而为随机变量,具有离散性质。分别用f(Y)和f(S)表示屈服强度和应力的概率分布密度函数,由概率分布密度函数的性质可知,两条概率密度曲线有相交的区域,即为产品或零件可能出现失效的区域,称为干涉区。应力强度干涉曲线如图1所示。
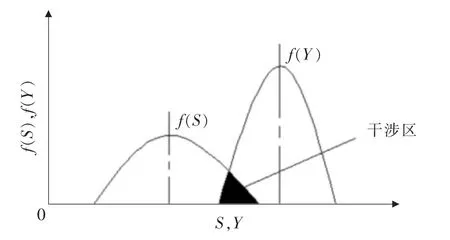
▲图1 应力强度干涉曲线
应力S和强度Y本身是某些变量的函数:

式中:si为影响应力的随机变量,如载荷情况、应力集中等;yi为影响强度的随机变量,如材料性能、工艺方法、使用环境等。
如果产品的应力S大于强度Y,则其不能完成规定功能,称为失效。建立结构功能函数Z(X)=Y-S,则结构的可靠度就是计算Z≥0的概率。即:

式中:X为影响屈服强度及应力的各变量组成的向量。
3 工程案例
3.1 案例概况
某在役5 000 m3丙烷球罐的设计压力P为2.5 MPa,设计温度为50℃,容器内径R为10.6 m,壁厚T为0.048 m。容器材料为Q345R,弹性模量E为210 GPa,泊松比为0.3,屈服强度YIES为345 MPa。现对球罐壳体进行可靠性分析。
3.2 有限元分析模型
应用ANSYS软件PDS模块进行球罐可靠性分析时,需要采用APDL命令流进行参数化建模。在不影响球罐受力的情况下,忽略开孔及接管等结构。由于球罐结构的高度对称性,因此将其简化为1/2轴对称平面模型,设定轴对称选项并划分网格。在X=0节点上施加UX=0的位移约束,在Y=0节点上施加UY=0的位移约束,内壁施加均匀压力载荷P=2.5 MPa,并在Y方向上施加惯性载荷g=9.8 m/s2。求解后得到球罐的应力云图,如图2所示。

▲图2 球罐应力云图
3.3 可靠性计算
将球罐等效应力按升序排列并提取最大等效应力MAXSTR,定义结构函数Z=YIES-MAXSTR,并与之前的命令流形成完整的可靠性分析文件。由上文可知,球罐可靠度就是求Z≥0的概率。进入ANSYS软件PDS模块,指定可靠性分析文件,并定义随机输入变量和输出变量Z。随机输入变量及其分布类型见表1。

表1 随机输入变量及分布类型
3.4 可靠性分析结果
采用蒙特卡罗法进行10 000次抽样模拟后,得到可靠性分析结果。
对模拟结果进行精确度检验。如图3所示,由输出变量Z的抽样过程可知其平均值已经收敛,由此表明10 000次抽样已经足够准确求出球罐的可靠度。
在置信度97.5%的情况下,Z≤0的概率为1.39%,则当前该球罐的可靠度为98.61%。
图4所示为各参数均值的灵敏度分析结果,可知工作压力及屈服极限对可靠度的影响较大,而壁厚及半径的影响较小。屈服强度和壁厚对可靠度为正影响,这是因为材料屈服强度增大,提高了球罐的应力承受能力,而壁厚增大,降低了球罐的整体应力水平,从而使可靠度升高。内径和工作压力对可靠度为负影响,这是因为球罐的内径或压力增大,会导致球罐等效应力增大,从而降低可靠度。
顺序变换有关随机参数,进行各参数的灵敏度分析,结果见表2。可知四个参数的标准差 σR、σT、σP、σY对球罐可靠度均为负影响,即球罐的可靠度随四个标准差的増大而减小。这是因为在参数均值不变的情况下,标准差增大致使分散性有所增强,因此球罐的可靠度降低。
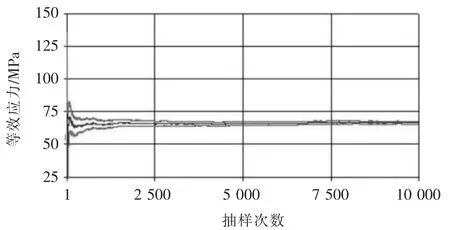
▲图3 最大等效应力抽样过程

▲图4 参数均值灵敏度分析结果
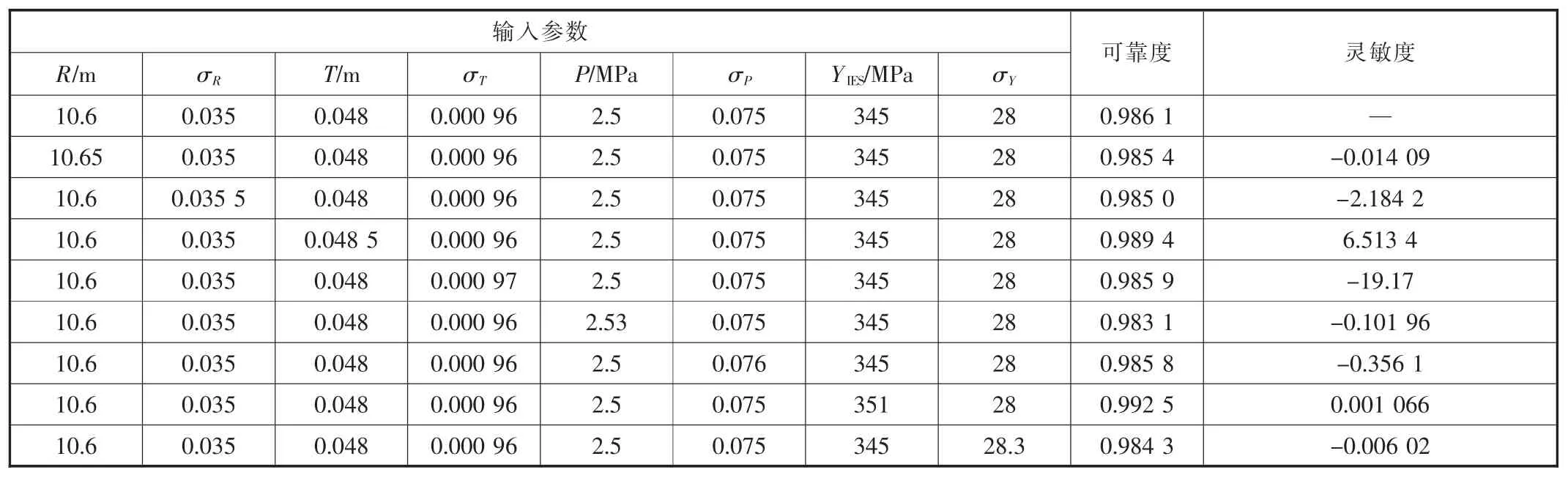
表2 随机参数灵敏度分析结果
4 结束语
根据可靠性分析理论和有限元分析技术,应用ANSYS软件PDS模块对处于运转中的球罐进行了可靠性分析,获得了球罐的可靠度及各设计参数的灵敏度结果,显示了设计参数对球罐可靠度的影响程度。
当今压力容器设计已有一整套相对比较完整的规范和标准,这些规范和标准都已经或正在实施中。笔者提出的包括概率设计在内的有限元分析设计方法,为压力容器的设计与分析带来了一种新的方法,主要适用于已处在运转工作状态的压力容器维护检测的可靠性分析。
笔者所述可靠性检测分析方法能为复杂结构压力容器的优化设计及可靠性分析提供有效依据,尤其是对处于运转中的压力容器,能有效进行维修检测可靠性分析,对特定压力容器的试验具有指导作用。
