利用TLE数据判别天宫一号目标飞行器姿态

张 炜，崔 文，田 鑫，雷 园，刘 兴

(西安卫星测控中心，西安 710043)

1 引言

天宫一号是我国第一个目标飞行器和空间实验室，于2011年9月29日发射入轨，先后与神舟八号、神舟九号、神舟十号成功对接完成相关任务。2016年3月16日天宫一号目标飞行器正式终止数据服务，无法继续维持正常运行轨道，在大气阻力的影响下轨道不断衰减，最终于2018年4月2日8时15分左右再入大气层。轨道寿命末期天宫一号重约8 t，是我国非受控再入的第一个超大型航天器。大质量航天器在再入过程中并不能被完全烧毁，仍有10%～40%的残骸返回地球表面[1]，对地表的生命群体、建筑设施、生态环境等具有很大威胁，因此有必要进行精确的再入时间和落点预报[2]。

天宫一号的再入过程有以下几个特点：

1) 再入过程中飞行器姿态经历了稳定到不稳定、缓慢翻滚到快速翻滚的变化；

2) 再入过程中太阳活动基本处于极低水平；

3) 再入的最后阶段地磁环境处于持续扰动状态。

因此，天宫一号的再入案例对于开展轨道动力学和再入预报研究具有特殊意义。

大气阻力是即将再入航天器所受的最主要非保守摄动力，精确的面质比及合理的大气阻力特性建模是准确计算大气阻力加速度、预报再入时间的关键[3]。对于绝大多数空间目标，其准确外形、质量、姿态和表面材料等都是未知的，分别确定大气阻力系数、迎风面积和质量难度很大，因此通常引入弹道系数B进行统一处理，弹道系数B的定义为式(1)[4]：

(1)

其中，CD为大气阻力系数，A为迎风面积，m为质量。

大部分非受控再入航天器都处于姿态失控状态，研究天宫一号在低轨甚至超低轨道情况下的轨道动力学特性，有必要先判别飞行器姿态，针对不同研究目的选择不同姿态阶段的数据。传统的姿态判别方法是基于目标的雷达特征(包括窄带雷达散射截面积、一维距离像、二维/三维雷达图像等)[5]或光学特征[6]进行判别，这些判别方法对观测条件具有较高的要求，且一个地基观测弧段往往只有几分钟，在航天器翻滚周期大于观测弧段时长的情况下往往难以准确判断飞行器姿态变化，因此需要其他辅助判别方法。

本文从姿态变化引起迎风面积变化这一特点出发，提出一种基于弹道系数的天宫一号目标飞行器姿态判别方法：使用美国战略司令部公开发布的双行根数(Two Line Element，TLE)作为数据源，首先对TLE数据进行筛选，剔除精度较差的异常TLE，然后基于多组TLE数据使用最小二乘法计算弹道系数，对天宫一号的飞行姿态进行判别。

2 TLE数据预处理

本文选择美国战略司令部发布的TLE[7]作为数据源。为了比较数据服务终止前后弹道系数的变化，选择2015年1月1日作为数据起始时间。由于数据服务终止前天宫一号可能发生轨道机动，发布的TLE可能包括精度差甚至错误结果，因此TLE使用前需先进行预处理，检测轨道机动，并剔除异常TLE。根据大型空间目标TLE根数精度的特点，预处理按以下几步进行[8]：

1) 剔除发布后立即被修正的TLE；

2) 剔除B*为负的TLE(B*为TLE中的阻力系数项)；

3) 轨道机动检测；

4) 基于平运动变化剔除异常TLE。

本节主要介绍轨道机动检测和基于平运动变化剔除异常TLE的方法。

低轨航天器的轨道机动一般分为轨道面内机动和轨道面外机动；轨道面内机动会引起平运动、半长轴、能量和(或)偏心率的突然变化，而轨道面外机动改变的则是卫星轨道的倾角或升交点赤经[9]。比较相邻两段数据的轨道特征量(半长轴、能量或倾角等)，若特征量出现较大变化，则认为两段数据之间发生轨道机动[10]。图1展示了基于TLE检测轨道机动方法的基本原理，本文将连续6条TLE数据组成数据段，使用最小二乘法拟合对应一阶多项式，依据连续两段数据的多项式变化进行轨道机动检测。检测到2015年1月1日以后天宫一号共进行两次轨道机动，一次发生在2015年4月10日，另一次发生在2015年12月16日，均为轨道面内轨道机动。

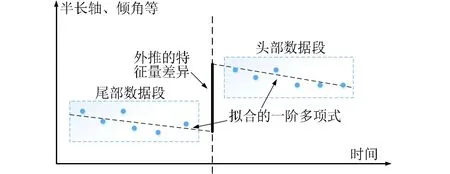
图1 轨道机动检测的基本原理Fig.1 The basic principle of maneuver detection

基于平运动变化剔除异常TLE是轨道机动检测方法的简化和延伸。使用平运动n作为特征量，尾部数据段长度仍为6，而头部数据段长度为1，仅拟合尾部数据段的多项式，计算平运动的相对变化量TR如式(2)[8]：

(2)

其中，Δnc为头部数据n与外推值之间的差，Δnp为多项式外推至头部数据历元时n的变化量。方法如图2所示。

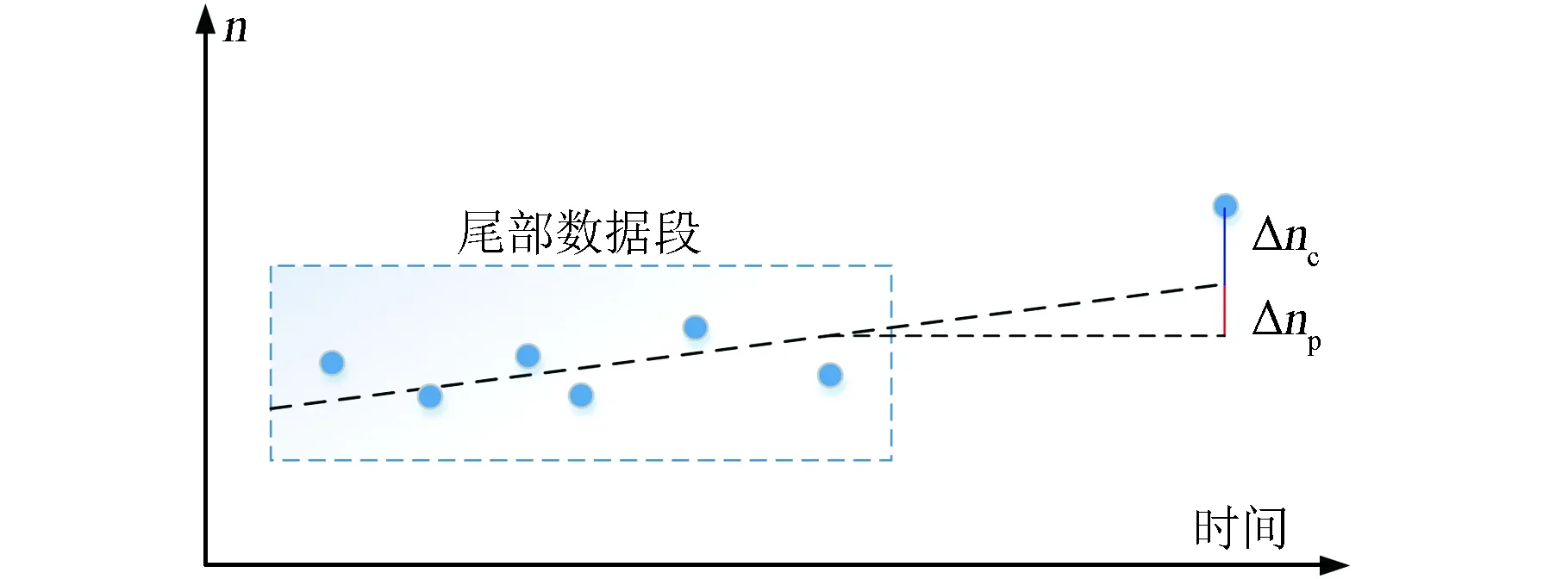
图2 基于平运动变化的异常TLE剔除方法Fig.2 The outlier filtering method based on mean motion

本文TR的阈值取为0.6，即认为TR大于0.6的TLE是异常数据。比较预处理前后天宫一号TLE序列的B*，结果如图3所示。可以看出，预处理后B*序列的平滑性有了很大改善，认为预处理后天宫一号的TLE整体轨道精度有了很大改善。

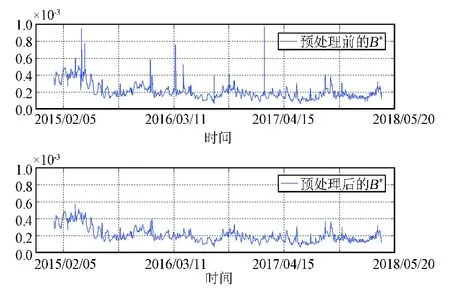
图3 预处理前后天宫一号的B*序列Fig.3 The pre and post preprocess of B* of TIANGONG-1

3 基于TLE的弹道系数计算方法

TLE数据并不能直接提供天宫一号的弹道系数信息，较为相关的是B*项，B*与弹道系数B之间的关系可以近似表示为[11]：B=12.741×B*，但是此结果与真实弹道系数仍存在较大误差。基于TLE计算航天器的弹道系数，最简单的办法是根据两条TLE的半长轴的衰减进行计算，即通过调整弹道系数，使较老TLE预报至较新TLE历元时预报的半长轴与较新TLE的实际半长轴一致。弹道系数的修正可以表示为式(3)[12]：

(3)

其中，ΔaTLE为两条TLE的半长轴实际衰减量，ΔaB为使用初始弹道系数B0进行轨道预报的半长轴衰减量，B′为修正后的弹道系数。这种方法的问题是TLE精度对弹道系数精度影响很大。本文对此方法进行改进，使用最小二乘方法对N(N≥3)条TLE进行弹道系数的拟合，使各TLE的实际半长轴与计算半长轴之间的误差最小。基本过程如下：

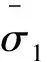
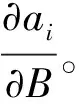
(4)

其中，ρ为大气密度，本文使用MSIS-90大气模型计算，V为航天器相对于大气的运动速度，e为偏心率，f为真近点角，ωE为地球自转角速度，i为轨道倾角，μ为引力常数，M为平近点角。

4) 最后一条TLE计算结束后，使用公式(5)计算弹道系数修正值；

(5)

大气阻力仅有长期作用效果，且采用开普勒平根数作为根数系统，因此进行轨道积分时的积分步长可取为轨道周期的整数倍，以提高计算效率。

4 姿态判别结果

弹道系数是空间目标的固有属性，不同空间目标的弹道系数可能会有较大差异，同一空间目标在不同姿态下弹道系数也可能不同。

本文的弹道系数是基于轨道数据的解算结果，弹道系数吸收了轨道误差、大气环境建模误差及航天器姿态变化等，因此解算的弹道系数并不是常值。对于天宫一号而言，预处理后的TLE用于解算弹道系数时精度已经足够，对弹道系数精度影响很小；大气环境建模的误差在大气环境平静时影响不超过10%，扰动期间影响可能超过20%[13]，是姿态稳定时造成弹道系数波动的最主要因素；空间目标姿态稳定时面质比不发生变化，快速翻滚的航天器在翻滚方向不发生改变的情况下也可以认为姿态对弹道系数无影响。天宫一号外形结构比较复杂，姿态变化引起的弹道系数变化较为明显。使用前文所述方法对2015年1月1日起美国战略司令部公开发布的TLE进行预处理及弹道系数计算，结果如图4所示。

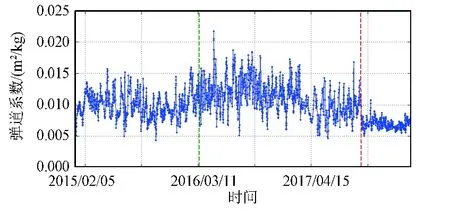
图4 天宫一号的弹道系数结果Fig.4 The ballistic coefficient estimation results of TIANGONG-1

其中，绿色虚线为天宫一号终止数据服务时间，即2016年3月16日，红色虚线前后(大约2017年10月8日)天宫一号的弹道系数有明显差异。分段进行天宫一号弹道系数分析：

1) 天宫一号数据服务终止前后

从图5可以看到，数据服务终止前弹道系数的均值约为0.0105 m2/kg，数据服务终止后至红色虚线所示日期前弹道系数的均值约为0.0113 m2/kg，前后相差不到8%，差异主要由空间环境周期性变化引起。数据服务终止前后天宫一号的弹道系数变化特点基本一致，即使空间环境稳定也存在周期性变化，变化周期约为5天，初步判断天宫一号数据服务终止后姿态未发生明显变化。

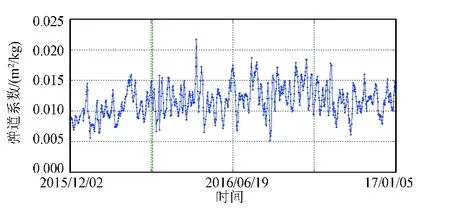
图5 天宫一号数据服务终止前后弹道系数特性Fig.5 The characteristic of ballistic coefficients of TIANGONG-1 before and after data service termination

2) 2017年10月8日前后

2017年10月5日至10月13日天宫一号的弹道系数如图6所示，期间天宫一号的弹道系数逐渐减小，10月6日前天宫一号的弹道系数均值约为0.0113 m2/kg，10月12日后天宫一号弹道系数的均值约为0.0069 m2/kg。期间太阳活动及地磁环境均稳定，无磁扰、磁暴等异常情况发生，可以排除弹道系数变化由大气环境建模误差引起。分析认为天宫一号姿态变化引起弹道系数持续减小，2017年10月6日至10月12日，天宫一号姿态逐渐变化。

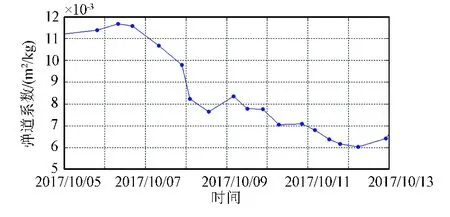
图6 2017年10月5日至10月13日天宫一号的弹道系数Fig.6 The ballistic coefficients of TIANGONG-1 between Oct. 5 and Oct. 13, 2017

图7 2017年10月12日后天宫一号的弹道系数结果Fig.7 The ballistic coefficients of TIANGONG-1 after Oct. 12, 2017

3) 2017年10月12日后

图7为2017年10月12日后天宫一号的弹道系数结果及地磁指数情况。可以看出，弹道系数与地磁环境具有明显相关性，可以认为地磁变化是造成弹道系数变化的主要原因，这是因为现有的大气密度模型不够精确，地磁环境扰动情况下的大气密度计算误差大于平静时期的大气密度计算误差。期间天宫一号的翻滚速度可能继续加快，但由于翻滚方向不变的情况下平均等效迎风面积不变，无法再基于弹道系数判断翻滚速度变化情况。

综上，可以将天宫一号的姿态变化分为以下几个阶段：

1) 稳定阶段：2016年3月16日至2017年10月6日。天宫一号的弹道系数变化特点与终止数据服务前基本一致，认为天宫一号处于稳定状态；

2) 逐渐变化阶段：2017年10月6日至2017年10月12日。天宫一号的姿态从稳定转为缓慢翻滚，弹道系数逐渐减小；

3) 翻滚阶段：2017年10月12日以后。天宫一号处于持续翻滚状态，翻滚速度变化对弹道系数的影响很小，弹道系数基本稳定。

5 结论

本文从姿态变化引起迎风面积变化这一特点出发，使用美国战略司令部公开发布的双行根数TLE作为数据源，提出基于弹道系数的天宫一号姿态判别方法，判别出天宫一号姿态稳定、逐渐变化及翻滚三个阶段。实测的雷达特征数据发现，天宫一号于2017年10月中旬开始有明显翻滚现象，结合本文的分析结果，可以将天宫一号姿态变化的时间精确到10月6日至10月12日之间。本文提出的方法可以作为传统姿态判别方法的有效补充。

值得指出的是，本文提出的方法也存在一定局限性。在飞行器结构较为简单、姿态失稳后弹道系数变化不明显的情况下，可能无法进行准确判断。