一种微穿孔板消声器传递损失

翟 华 ，王 震 ，李国峰 ，吴友林

（1.合肥工业大学 工业与装备技术研究院，安徽 合肥 230009；2.合肥工业大学 机械工程学院，安徽 合肥 230009；3.安徽均益金属科技有限公司，安徽 池州 247100）

锻压装备中大功率电机引起的噪声一直是用户企业环保减噪建设的重要挑战，其噪声是以高频为主的宽频带噪声。本文针对变频高压噪声提出一种新型微穿孔板消声器结构，结合一维平面波理论和微穿孔板吸声结构理论[1-3]，推导出该消声器传递损失的理论计算公式，并利用LMS Virtual lab对消声器进行了三维有限元仿真计算。将理论计算结果与有限元仿真分析结果进行对比，分析了微穿孔板消声器声学性能，为微穿孔板消声器设计提供了理论依据。

1 微穿孔板吸声结构理论

1.1 微穿孔板吸声体结构

微穿孔板吸声结构是将穿孔直径在0.1mm～1mm的穿孔板固定在一固体前面，形成一种声质量低、声阻高的共振吸声结构[4]。其吸声机理为：当声波入射到微穿孔板上时，空气在小孔中通过反复摩擦，消耗声能，从而实现消声作用。

微穿孔板吸声体及其等效电路如图1所示。这种吸声结构的声学特性参数主要有：微孔直径d、板厚度t、穿孔率p、板后空腔深度D。

图1 微穿孔板吸声体及其等效电路

1.2 微穿孔板吸声结构性能

微穿孔板吸声结构的吸声性能可由其声阻抗率Z 表示[5]：

ZMPP为微穿孔板的声阻抗率：

式中：R——穿孔板声阻率；

M——声质量率；

X——穿孔常数；

Ρ——空气密度；

Μ——运动粘滞系数。

ZD为板后空腔的声阻抗率：

2 微穿孔板消声器的研究

2.1 新型微穿孔板消声器结构模型

抗性消声器如扩张式消声器，不仅吸收频带窄，而且对高频的吸收效果不明显。为了提高抗性消声器对高频噪声的吸收，通常在消声器中加装阻性吸声材料，构成阻抗复合式消声器[6]，但附加材料会对空气的洁净度产生影响，同时也不能适用于高温、高湿等极端环境，如对空气洁净度有一定要求的燃料电池高压旋涡风机的降噪，以及高温环境下的锅炉排气降噪等。为了解决这个问题，本文提出了一种新型微穿孔板消声器，其结构示意如图2所示。

图2 微穿孔板消声器结构示意图

该消声器的进、排气管由左右两个插入管构成，进、排气管分别以一定长度插入到一段扩张腔内，左、右插入管及扩张腔轴线共线，在距扩张腔左、右两端壁面一定距离分别加装两块微穿孔板，微穿孔板与扩张腔端壁面以及两者之间形成的空腔共同构成微穿孔板吸声结构。

2.2 微穿孔板消声器传递损失理论计算

该消声器传递损失的理论计算基于一维平面波假设、管道声学理论及"微穿孔板吸声结构"理论。首先根据任意位置的速度势求出该点的声压和速度，再根据各个截面处声压相等和体积速度连续条件列出相应方程，进而求出消声器的传递损失[7]。为了方便传递损失的计算推导，对双极微穿孔板消声器的各截面进行了定义，其示意如图3所示。

取突变截面Ⅰ位置为x轴初始位置：即x=0；P1+为消声器入射声压，P1-为插入管S1后端声负载产生的反射声压；P2+、P2-分别为靠近突变截面Ⅰ右P3+、P3-侧的入射声压以及后端声负载产生的反射声压；P3+、P3-分别为扩张腔内靠近突变截面Ⅰ左侧的入射声压以及后端声负载产生的反射声压；在x=0处，根据声压连续条件和体积连续条件可知[8]：

图3 微穿孔板消声器

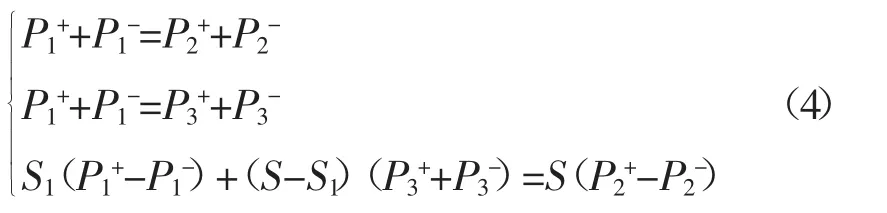
声压P2在扩张腔内从突变截面Ⅰ传播L2距离到突变截面Ⅱ，之后分为两部分，一部分从右插入管传出，另一部分透过突变截面Ⅱ继续在扩张腔内向前传播；由管内声场条件可知，在靠近突变截面Ⅱ左侧，入射声压变为 P2+e-jωl2，反射声压变为 P2-ejωl2；在靠近突变截面Ⅱ右侧的右插入管内，由于消声器尾部无声负载，因此只有入射声压P5+，无反射声压；P4+、P--分别为扩张腔内靠近突变截面Ⅱ右侧的入射声压以及后端声负载产生的反射声压；在x=L2处，根据声压连续条件和体积连续条件可知：

在扩张腔内，声压P3向左传播L1后进入到左微穿孔板吸声结构，并由左微穿孔板吸声结构产生反射；在 x=-L1处，根据管内声场条件，P3+变为 P3+ejωl1，P3-变为 P3-e-jωl1；在x=-L1处，根据马大猷先生的微穿孔板吸声结构理论，微穿孔板吸声结构板前声压条件[9]：

Z1为左微穿孔板吸声结构的声阻抗率。

消声器传递损失计算公式[9]：

式中：wi为入口声功率

wr为出口声功率

综合式（1）～（7），利用 MATLAB 软件可以计算出微穿孔板消声器传递损失。

2.3 微穿孔板消声器有限元仿真分析

在声学仿真软件LMS virtual lab中建立微穿孔板消声器的有限元模型，并对建立的有限元模型进行有限元计算。为了避免微穿孔板上微孔网格质量差及计算量大的缺点，本文利用传递导纳法[13]对微穿孔板进行建模。如图4所示，微穿孔板两侧的振动速度和声压的关系可用以下公式表达：

式中：V1、P1，V2、P2分别为微穿孔板内外侧质点振动速度和声压。

图4 双极微穿孔板消声器有限元模型

3 结果与讨论

为了验证微穿孔板消声器传递损失的数学理论模型，分别对三种不同腔深（5a）D1=40mm、（5b）D1=80mm、（5c）D1=120mm的双极微穿孔板消声器的传递损失进行了理论计算和有限元仿真计算（其他参数见表1），并将理论计算结果与三维有限元分析结果进行比较。

表1 双极微穿孔板消声器结构参数

消声器的传递损失曲线如图5所示。图中表示了三种不同腔深的双极微穿孔板消声传递损失理论计算结果与三维有限元仿真分析结果对比。

图5 不同腔深双极微穿孔板消声器传递损失曲线

对于（5a）D1=40mm，在 0～2000Hz内，双极微穿孔板消声器器传递损失理论计算结果与仿真结果基本吻合，理论计算值共振峰较仿真值略有左移，当频率大于2000Hz，二者存在明显差异，是因为噪声频率超过消声器截止频率，一维平面波理论不在适用造成的。

对于（5b）D1=80mm、（5c）D1=120mm，随着腔深的增加，在0～2000Hz，双极微穿孔板消声器理论计算结果与仿真结果与（5a）D1=40mm类似，同时在2000～30000Hz时，二者的吻合程度明显好于（5a）D1=40mm的情况，是因为随着腔深的增加，微穿孔板吸声结构成为影响消声器吸收噪声的主要因素，提高了消声器的截止频率，使理论计算结果在高频段更准确。

此外，综合（5a）D1=40mm、（5b）D1=80mm、（5c）D1=120mm可以看出，随着腔深的增加，双极微穿孔板消声器的共振峰值向高频移动，在高频区域的吸声性能略有提升，并且传递损失曲线更加平稳，总体吸声频带有所改善。

从图中可以看出，双极微穿孔板消声器传递损失理论计算结果和有限元仿真结果能够很好吻合。

4 结论

（1）针对锻压装备中大功率电机引起的噪声，提出微穿孔板消声器。

（2）基于一维平面波假设，管道声学理论和“微穿孔板吸声结构”理论对提出的微穿孔板消声器的递损失进行了理论推导，并通过与三维有限元仿真分析结果进行对比，验证了数学理论模型的准确性，为微穿孔板消声器的设计提供了理论预估基础。

（3）分析了腔深双极微穿孔板消声器传递损失的影响，通过改变不同的腔深，可以得到不同的共振频率，并且随着腔深的增加，消声器在高频段的吸声性能有所改善，为适应不同场合的消声器设计提供理论指导。